Отношение порядка

Определение. Отношение Р на множестве А называется отношением порядка если оно антисимметрично и транзитивно. Часто обозначается символом .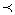

Если к тому же оно:

1) рефлексивно, то называется частичным или нестрогим порядком (≤);

2) антирефлексивно, то называется отношением строгого порядка (<).

Определение. Пусть на множестве А задано отношение порядка 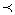, если для любых двух элементов a и b этого множества имеет место a 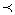b или b 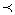a, то элементы называются сравнимыми, в противном случае несравнимыми.

Определение. Частичный порядок на множестве А называется линейным или цепью, если любые два элемента этого множества сравнимы.

Множество А, на котором определен частичный (линейный) порядок, называется частично упорядоченным множеством (ч.у.м) (линейно упорядоченным множеством (л.у.м)). Обозначается (А, ).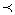

Пример 1.2.11 - A={a,b,c}. P={(a,a),(a,b),(b,b),(c,c)} – отношение частичного порядка (т.е. рефлексивно, антисимметрично, транзитивно), что легко проверить по его матрице [P]= 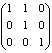. Р не является линейным порядком, т.к. a и c, b и c не сравнимы.

Примерами линейно упорядоченных множеств являются множества N, Z, Q, R, где определён естественный порядок.

Определение. Элемент a упорядоченного множества А называется наибольшим (наименьшим), если в А нет таких x, что x<a (x>a). Л.у.м. называется вполне упорядоченным множеством (в.у.м), если любое его непустое подмножество имеет наименьший элемент.

Пример 1.2.12 - (N; ≤) – в.у.м. ([0;1]; ≤) – не является в.у.м., т.к., например, (0;1] [0;1], но (0;1] не содержит наименьшего элемента.

Определение. Рассмотрим ч.у.м. (Х,≤). Говорят, что элемент у покрывает элемент х, если х≤у и не существует такого элемента z, что х<z<y.

В случае конечного множества Х, ч.у.м. (Х,≤) можно представить в виде схемы, в которой каждый элемент изображается точкой на плоскости. Если у покрывает х, то точки х и у соединяют отрезком, причём точку, соответствующую х, располагают ниже точки у. Такие схемы называют диаграммами Хассе.

Пример 1.2.13 - 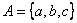. Рассмотрим ч.у.м. (Р(А), ) = 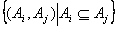, где Р(А) булеан А. Диаграмма Хассе для (Р(А), ) на рисунке 1.2.4.

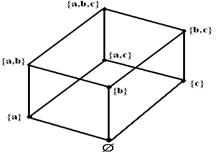
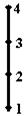
Рисунок 1.2.4 Рисунок 1.2.5

Пример 1.2.14 - Для л.у.м. 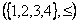с обычным отношением порядка на множестве натуральных чисел, не превосходящих четырёх, диаграмма Хассе изображена на рисунке 1.2.5.

Дата добавления: 2014-12-27