Отношения. При решении различных задач практики часто требуется учитывать связи или отношения между элементами одного и того же или разных множеств

При решении различных задач практики часто требуется учитывать связи или отношения между элементами одного и того же или разных множеств. Например, если имеем множество стран мира, то можно рассматривать между странами такие отношения: «в стране x населения больше, чем в стране y» или «страны х и у имеют общую границу»; если имеем множества мужчин, женщин и детей, то можно рассматривать отношение «х и у родители z» и т.д.

Определение.n-местным отношением P (n-местным предикатом) на множествах А₁,А₂,…,А_n называется любое подмножество прямого произведения этих множеств: P A₁×A₂×…×A_n и P={(x₁,x₂,…x_n)| A₁,…,x_n A_n}. То, что элементы x₁,x₂,…x_n связаны соотношением Р записывается (x₁,…,x_n) P или P(x₁,…,x_n). Если P Aⁿ, то Р – n-местное отношение на множестве А. n=1, то P 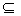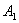- одноместное (унарное) отношение или свойство; n=3, то P 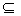A₁×A₂×A₃ – трёхместное (тернарное) отношение.

Наиболее часто встречаются и хорошо изучены бинарные отношения (n=2) или соответствия P A₁×A₂ или P={(x,y)|x A₁, y A₂}. Записывают P(x,y) или xPy. Например, вместо <(x,y) или (x,y) < записывают x<y. Далее будем рассматривать бинарные отношения, называя их просто отношениями.

Определение.Областью определения отношения Р (обозначается D_P) называется D_P ={x| (x,y) P для некоторого y}; областью значений (обозначается E_P) называется E_P ={y| (x,y) P для некоторого x} (т.е. D_P- это множество первых координат пар Р, E_P – вторых).

Отношение можно задать перечислением элементов, характеристическим свойством, графически, с помощью матриц.

Бинарные отношения на конечных множествах обычно задаются либо списком пар, либо матрицей, либо графически.

Определение.Пусть A={a₁,a₂,…,a_m}, B={b₁,b₂,…,b_n} и P A×B. Матрица [P] =(p_ij), размера m×n, называется матрицей отношения Р, если 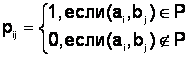, i=1,2,…,m; j=1,2,…,n.

Пример 1.2.1 - A₁={1;2}, A₂={3;4}. A₁×A₂={(1,3), (1,4),(2,3),(2,4)}.

P₁={(1;3)}, P₂={(1;3);(1;4);(2;3)}, тогда , .

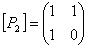Пример 1.2.2 - A={2,3,4,5,6,7,8}; P={(x,y) | x,y A, y делится на x, x ≤3} = {(2,2) (2,4),(2,6),(2,8),(3,3),(3,6)}.

Графическое задание Р, где по осям координат отмечены элементы множества А, а на плоскости –точки с координатами (x,y), такие что (x,y) P:

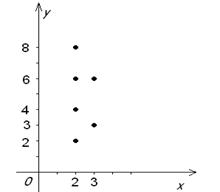
Рисунок 1.2.1

Матричное задание Р: .

Рассмотрим примерыдругих способов графического задания отношений: пусть A={a,b,c}, B={1,2,3}, P₁={(a,2),(b,1),(c,2)}, P₂ ={(a,b),(b,b),(c,a)}. На рисунке 1.2.2 показаны отношение P₁ между множествами А и В и отношение P₂ на множестве A.

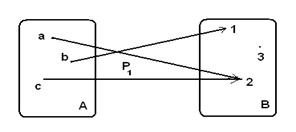
Рисунок 1.2.2

Определения. Пусть P A×B, P={(a,b)|a A, b B}.

а) P^-1 – обратное Р 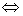P^-1 = {(b,a)|(a,b) P}, P^-1 B×A;

б) - дополнение P 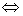={(a,b)|(a,b) P}, A×B;

в) I – тождественное отношение на множестве А (иногда обозначается

id ). I={(a,a)|a A}, I 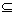A² (называют также диагональю в A², т.к. его матрицей является единичная матрица);

г) U – универсальное отношение 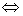U ={(a,b)|a A и b A}, т.е. U=A².

Определение. Композицией (произведением) бинарных отношений

P₁ A×B и P₂ B×C (обозначается P₁ P₂) называется отношение

Р=P₁ P₂ = {(a,c)|a A, c C и b B, что (a,b) P₁ и (b,c) P₂}.

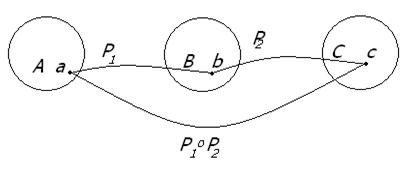
Рисунок 1.2.3

Пример 1.2.3 - A={1,2,3}, B={x,y}; C={ ■, ▲, ●, *}.

Пусть P₁={(1,x),(1,y),(3,x)}, P₂={(x,■),(x,▲),(y,●),(y,*)}, тогда

P₁ P₂={(1,■),(1,▲),(1,●),(1,*),(3,■),(3,▲)}.

Пример 1.2.4 - P₁={(x,x+2)|x Z⁺}, P₂={(x,x²)|x Z⁺}, тогда

P₁ P₂={(x,(x+2)²)| x Z⁺}, P₂ P₁={(x,x²+2)| x Z⁺}, где Z⁺ множество целых положительных чисел.

Теорема. Для любых бинарных отношений P, Q, R выполняются следующие свойства:

а) (P^-1)^-1=P;

б) (P Q)^-1=Q^-1 P^-1;

в) (P Q) R=P (Q R).

Дата добавления: 2014-12-27