
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Множества
Элементы теории множеств.
ДИСКРЕТНАЯ МАТЕМАТИКА
Учебное пособие
для студентов всех форм обучения специальностей
5B0704 – Вычислительная техника и программное обеспечение,
5B0703 – Информационные системы
Алматы 2011
УДК 519.6 (075.8)
ББК 22.176 Я 73
А 91 Дискретная математика:
Учебное пособие /Л.Н. Астраханцева;
АУЭС. Алматы, 2011.- 78 с.
ISBN – 601 – 7098 – 78 - 0
Пособие представляет собой переработанные и дополненные лекции по дискретной математике, читаемые автором в АУЭС, оно включает четыре раздела, традиционно изучаемые в курсе дискретной математики: элементы теории множеств и отношений, элементы математической логики, теории графов и комбинаторики. Содержание разделов взаимно связано друг с другом. В доступной форме изложены основные теоретические сведения, приведены примеры и решённые задачи, помогающие усвоить и закрепить изучаемый материал. Пособие предназначено для студентов всех форм обучения специальностей 5В070400 – Вычислительная техника и программное обеспечение и 5В070300 – Информационные системы.
Ил. 72, табл. 14, библиогр. – 16 назв.

ББК 22.176 Я 73
РЕЦЕНЗЕНТ: КазНУ, канд. физ.-мат. наук, доц. У.К. Койлышов.
АУЭС, канд. физ.-мат. наук, доц. М.Ж. Байсалова.
Печатается по плану издания Министерства образования и науки Республики Казахстан на 2011г.
© НАО «Алматинский университет энергетики и связи», 2011г.
Понятия множества и элемента множества являются первичными (т.е. не определяемыми с помощью других, более простых понятий) такими, как, например, точка и прямая. Под множеством понимается совокупность некоторых объектов (предметов), которые называются элементами множества. Элементы множеств различны. Приняты следующие обозначения: A, B, X,… - множества; a, b, x, x1, x2,…- элементы множеств; 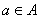 - элемент
- элемент 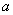 принадлежит А,
принадлежит А, 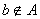 - элемент
- элемент 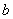 не принадлежит А; N – множество натуральных чисел; Z – множество целых чисел; Q – множество рациональных чисел; I - множество иррациональных чисел; R – множество действительных чисел; C – множество комплексных чисел; Ø – пустое множество (не содержит ни одного элемента).
не принадлежит А; N – множество натуральных чисел; Z – множество целых чисел; Q – множество рациональных чисел; I - множество иррациональных чисел; R – множество действительных чисел; C – множество комплексных чисел; Ø – пустое множество (не содержит ни одного элемента).
Конечные множества состоят из конечного числа элементов.
Бесконечные – из бесконечного числа элементов.
Способы задания множеств:
а) перечислением элементов, например, X={x1, x2,…, xn},
A = {2,4,5,6,8,…};
б) с помощью характеристического свойства: A={x| Р(x)}, гдеP(x) – свойство Р, которым обладает элемент x,например, A={x| x= 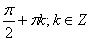 };
};
в) порождающей процедурой, которая описывает способ получения элементов из уже имеющихся элементов, например, множество M={1,2,4,8,16,…} можно задать так: 1) 1  M; 2)m
M; 2)m  M → 2m
M → 2m  M.
M.
Определения:
а) множество В называется подмножеством множества А (обозначается 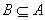 ), если каждый элемент множества В является элементом множества А:
), если каждый элемент множества В является элементом множества А: 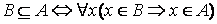 ,
,  - знак включения;
- знак включения;
б) множества А и В называют равными,если они состоят из одних и тех же элементов: 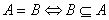 и
и 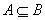 ;
;
в) если 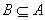 и
и 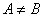 , то В является собственным подмножеством множества А:
, то В является собственным подмножеством множества А: 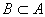 - строгое включение.
- строгое включение.
Заметим, что для обозначения отношения включения применяют как знак строгого, так и не строгого включения, как для собственных, так и для несобственных подмножеств. И только если требуется различить эти подмножества, различают и эти знаки. Не следует путать знаки  и
и  :
: 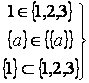 - верно,
- верно, 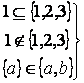 - не верно.
- не верно.
Множества могут быть элементами других множеств. Множество, элементами которого являются множества, иногда называют семейством и обычно обозначают прописными (готическимими) буквами латинского алфавита.Совокупность всех подмножеств множества А называется его булеаном или множеством-степенью. ОбозначаетсяР(А) или 2А. Таким образом, Р(А) = {B|B  A}. Булеан множества из n элементов, содержит 2n элементов.
A}. Булеан множества из n элементов, содержит 2n элементов.
Пример 1.1.1 - A={1,2,3},Р(А) ={Ø,{1},{2},{3},{1,2},{1,3},{2,3}, A}.
Р(А) содержит 8 элементов, 8=23 .
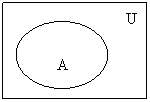
Обычно в конкретных рассуждениях элементы всех множеств берутся из одного достаточно широкого множества U, которое называется универсальным или универсумом. Для наглядного изображения множеств используют диаграммы Эйлера-Венна, на которых множества обозначаются точками кругов внутри прямоугольника, точки которого – множество U- универсум (см, рисунок 1.1.1, где A  Р(U)).
Р(U)).
|
Рисунок 1.1.1
|
|
Дата добавления: 2014-12-27; Просмотров: 449; Нарушение авторских прав?; Мы поможем в написании вашей работы!