
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Свойства отношений
|
|
|
|
Основные свойства матриц бинарных отношений
1 Пусть P,Q 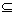 A×B, [P]=(pi,j), [Q]=(qi,j).
A×B, [P]=(pi,j), [Q]=(qi,j).
[P  Q] =(pij+qij) =[P]+[Q], где элементы матриц складываются по
Q] =(pij+qij) =[P]+[Q], где элементы матриц складываются по
правилам: 0+0=0, 1+0=0+1=1+1=1; [P  Q]=(pij*qij)=[P]*[Q], где элементы матриц перемножаются по обычным правилам: 0*0=0*1=0*1=0, 1*1=1.
Q]=(pij*qij)=[P]*[Q], где элементы матриц перемножаются по обычным правилам: 0*0=0*1=0*1=0, 1*1=1.
2 Если P  A×B, Q
A×B, Q  B×C, то [P
B×C, то [P  Q]=
Q]= 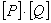 - обычное умножение матриц, но элементы матриц [P] и [Q] складываются и умножаются по правилам из свойства 1.
- обычное умножение матриц, но элементы матриц [P] и [Q] складываются и умножаются по правилам из свойства 1.
3 Если P-1 отношение, обратное к P, то [P-1]=[P]T.
4Если P  Q и [P]=(pij), [Q]=(qij), тогда pij≤qij.
Q и [P]=(pij), [Q]=(qij), тогда pij≤qij.
5 Если I–тождественное отношение, то 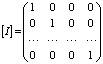 -единичная матрица.
-единичная матрица.
6 Если  - дополнение Р, то [
- дополнение Р, то [  ] равна матрице отношения Р, в которой нули заменены единицами и единицы нулями.
] равна матрице отношения Р, в которой нули заменены единицами и единицы нулями.
Пример 1.2.5 -
 ,
,  , тогда
, тогда  ;
;
 ;
; 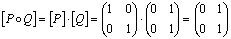 ;
;
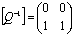 ,
,  .
.
Пусть P  A2. Отношение Р называется
A2. Отношение Р называется
а) рефлексивным 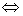
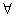 a
a  A (a,a)
A (a,a)  P;
P;
б) антирефлексивным 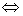
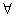 a
a  A (a,a)
A (a,a)  P или [(a,b)
P или [(a,b)  P
P 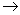 a≠b];
a≠b];
в) симметричным 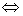
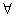 a,b
a,b  A (a,b)
A (a,b)  P
P 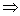 (b,a)
(b,a)  P;
P;
г) антисимметричным 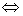
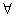 a,b
a,b  A (a,b)
A (a,b)  P и (b,a)
P и (b,a)  P
P 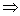 a=b;
a=b;
д) транзитивным 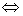
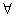 a,b,c
a,b,c  A (a,b)
A (a,b)  P и (b,с)
P и (b,с)  P
P 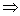 (a,c)
(a,c)  P.
P.
Заметим, что если
а) P-рефлексивное 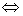 I
I  P, [P]=
P, [P]=  ;
;
б) P – симметричное 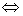 P=P-1, [P]=[P]T;
P=P-1, [P]=[P]T;
в) Р - антисимметричное 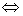 Р
Р  Р-1
Р-1  I, [P
I, [P  P-1]=[P]*[P-1], все элементы последней матрицы вне главной диагонали равны 0;
P-1]=[P]*[P-1], все элементы последней матрицы вне главной диагонали равны 0;
г) P- транзитивное 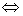 P
P  P
P  P, т.е. если [P
P, т.е. если [P  P]=(aij), [P]=(pij), то aij≤pij.
P]=(aij), [P]=(pij), то aij≤pij.
Пример 1.2.6 - Проверим, какими свойствами обладает отношение P = {(1,2),(2,3),(3,2)}  A2, А = {1,2,3}. Составим матрицу этого отношения [P]=
A2, А = {1,2,3}. Составим матрицу этого отношения [P]= 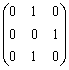 . P не рефлексивное, т.к. на главной диагонали матрицы нет единиц; P не симметричное, т.к. (1;2)
. P не рефлексивное, т.к. на главной диагонали матрицы нет единиц; P не симметричное, т.к. (1;2)  P, но (2;1)
P, но (2;1)  P или [P]≠[P]T; P не антисимметричное, т.к. (2;3)
P или [P]≠[P]T; P не антисимметричное, т.к. (2;3)  P, (3;2)
P, (3;2)  P, но 2≠3, или в матрице
P, но 2≠3, или в матрице  не все элементы вне главной диагонали нули; P не транзитивное, т.к., например, (1,2)
не все элементы вне главной диагонали нули; P не транзитивное, т.к., например, (1,2)  P, (2,3)
P, (2,3)  P, но (1,3)
P, но (1,3)  P.
P.
Пример 1.2.7 - Дано отношение P={(x;y)|x-y<1; x,y  Z}.
Z}.
а) Р рефлексивное, т.к. (x;x)  P(x-x=0<1);
P(x-x=0<1);
б) Р не симметричное, т.к., например, (2;4)  P, (4;2)
P, (4;2)  P;
P;
в) P антисимметричное, т.к. из (x-y)<1, y-x<1 следует x=y, потому, что если x≠y, то при x<y→x-y<0, при x>y→x-y>0, т.е. 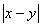 >0→
>0→ 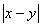 ≥1;
≥1;
г) P транзитивное, т.к. x-y<1, y-z<1 →x-z<1, действительно:
x-y<1

 +y-z<1 x-z=1
+y-z<1 x-z=1
 x-z<2 x-z<1,
x-z<2 x-z<1,
но x-z=1 противоречит условию x-y<1, остаётся x-z<1.
Многие отношения обладают определённым набором указанных выше свойств, и этот набор встречается так часто, что обладающие им отношения заслуживают специального названия и отдельного изучения.
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 343; Нарушение авторских прав?; Мы поможем в написании вашей работы!