
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Свойства операций над множествами
|
|
|
|
Операции над множествами.
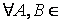 Р(U) следующие операции определяются так:
Р(U) следующие операции определяются так:
а) объединение (сумма) (обозначается  , +): А
, +): А  В = {x| x
В = {x| x  А или x
А или x  В}; б) пересечение (произведение) (
В}; б) пересечение (произведение) (  ,
,  ): А
): А  В = {x| x
В = {x| x  А и x
А и x  В};
В};
в) разность (А \ В; А – В): А \ В = {x| x  А и x
А и x  В};
В};
г) симметрическая разность или кольцевая сумма ( 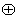 ,
,  , +): А
, +): А 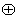 В=
В=
=(А \ В)  (В \ А) = {x| (x
(В \ А) = {x| (x  А и x
А и x  В) или (x
В) или (x  В и x
В и x  А)};
А)};
д)дополнение множестваА (  ):
):  ={x|x
={x|x 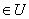 и x
и x  А}= U \ A. Иллюстрация
А}= U \ A. Иллюстрация
операций над множествами диаграммами Эйлера-Венна на рисунке 1.1.2.
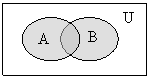

А  В A
В A  B
B


 А \ В А
А \ В А  В
В

Рисунок 1.1.2
Операции объединения и пересечения допускают обобщения:
A1  A2
A2  …
…  An =
An = 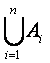 , A1
, A1  A2
A2  …
…  An =
An = 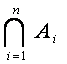 .
.
Для преобразования теоретико-множественных выражений, упрощения записей, доказательств теорем и свойств необходимо знать свойства операций над множествами. Рассмотрим важнейшие из этих свойств. Пусть задан универсум U, тогда 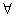 A, B, C
A, B, C  U выполняются свойства:
U выполняются свойства:
Т а б л и ц а 1.1.1
1 Идемпотентность
А  А=А А А=А А  А=А А=А
|
2 Коммутативность
А  В= В В= В  А А А А  В=В В=В  А А
|
3 Дистрибутивность
А  (В (В  С)=(А С)=(А  В) В)  (А (А  С) А С) А  (В (В  С)=(А С)=(А  В) В)  (А (А  С) С)
|
4 Ассоциативность
А  (В (В  С)=(А С)=(А  В) В)  С А С А  (В (В  С)=(А С)=(А  В) В)  С С
|
5 Свойство поглощения
А  (В (В  А)=А А А)=А А  (В (В  А)=А А)=А
|
6 Свойства нуля и единицы (констант)
А  Ø=А А Ø=А А  Ø= Ø
А Ø= Ø
А  U=U А U=U А  U= A U= A
|
7 Закон де Моргана
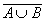 = =     = =   
|
8 Закон двойного отрицания (двойного дополнения или инволютивности)
 =A =A
|
9 Свойство дополнения
A   =U A =U A   = Ø = Ø
|
Доказать эти свойства можно либо с помощью диаграмм Эйлера-Венна, либо формальными рассуждениями, опирающимися на определение операций, например, докажем 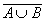 =
= 

 .
.
1 Доказательство с помощью диаграмм:
а)
 А
А  В
В 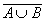
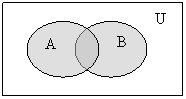

в) 

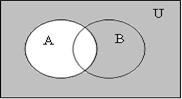




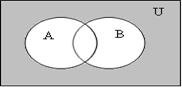
Рисунок 1.1.3
На последних рисунках в пунктах а) и в) отмечена одна и та же область, что доказывает тождество.
2 Докажем 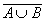 =
= 

 формальными рассуждениями.ем
формальными рассуждениями.ем
В формальных рассуждениях исходят из того, что А=В 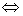 А
А  В и
В и
В  А, а последнее имеет место по определению отношения включения: А
А, а последнее имеет место по определению отношения включения: А  В
В 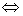 (x
(x  A
A 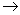 x
x  B) и В
B) и В  А
А 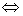 (x
(x  B
B 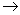 x
x  A), поэтому:
A), поэтому:
а) x 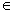
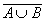
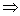 x
x 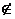 А
А  В
В 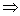 x
x  A и x
A и x  B
B 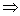 x
x 
 и x
и x 

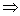 x
x 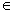


 ;
;
б) x 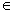



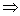 x
x 
 и x
и x 

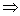 x
x  A и x
A и x  B
B 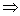 x
x 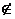 А
А  В
В 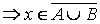 .
.
Теорема. Для любых множеств А и В следующие условия эквивалентны:
а) А  В;
В;
б) А  В=А;
В=А;
в) А  В =В;
В =В;
г) А \ В = Ø;
д) 
 В =U.
В =U.
В примере 1.1.2 свойства операций использованы для упрощения выражения.
Пример 1.1.2 - 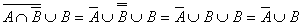 .
.
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 1848; Нарушение авторских прав?; Мы поможем в написании вашей работы!