
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лексикографический порядок
|
|
|
|
Лексикографический порядоклежит в основе упорядочения слов в различных словарях. Рассмотрим непустое множество символов Х={x,y,…}, называемое алфавитом. Словами будем называть конечные наборы написанных друг за другом элементов Х. Элемент xi слова x1,x2,…,xn назовём его i-ой координатой, а число n - его длиной.
Определение. Пусть W(X) – множество слов алфавита Х, пусть ≤ - отношение порядка на множестве Х, т.е. (Х,≤) – упорядоченное множество.
Отношение лексикографического порядка(обозначается 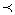 или L) на W(X) задаётся по правилу: x1,х2,…,xm L y1,y2,…,yn, если выполнено одно из условий: а) x1< y1; б) xi=yi
или L) на W(X) задаётся по правилу: x1,х2,…,xm L y1,y2,…,yn, если выполнено одно из условий: а) x1< y1; б) xi=yi 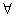 i:1≤i≤m, m<n; в) xi=yi
i:1≤i≤m, m<n; в) xi=yi 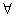 i:1≤i≤k, xk+1< yk+1.
i:1≤i≤k, xk+1< yk+1.
Функциональные отношения (функции)
Определение. Бинарное отношение f  А×В называется функциональным или функцией из множества А в множество В, если:
А×В называется функциональным или функцией из множества А в множество В, если:
а) (x,y1) 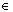 f, (x,y2)
f, (x,y2) 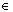 f → y1=y2 или
f → y1=y2 или 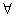 x
x 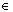 A
A  ! y
! y 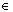 B, (x,y)
B, (x,y) 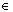 f;
f;
б) Df=A, Ef  B, где Df - область определения функции, Ef - область значений.
B, где Df - область определения функции, Ef - область значений.
В этом случае функцию иногда называют тотальной или всюду
определённой; если Df  A, то f называют частичной функцией или частично определённой. В математике, как правило, рассматривают тотальные функции и называют их просто функциями.
A, то f называют частичной функцией или частично определённой. В математике, как правило, рассматривают тотальные функции и называют их просто функциями.
Пример1.2.15 – 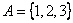 ,
, 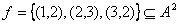 - функция, т.к.
- функция, т.к. 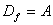 ,
,
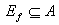 ;
; 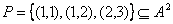 – не функция, т.к. содержит пары
– не функция, т.к. содержит пары 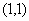 и
и 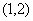 с одинаковыми первыми и разными вторыми элементами; отношение
с одинаковыми первыми и разными вторыми элементами; отношение 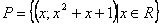 - функция, т.к. из того, что
- функция, т.к. из того, что 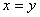 следует
следует 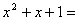
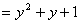 ;
; 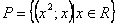 – не функция, т.к. содержит пары с одинаковыми первыми и разными вторыми элементами, например,
– не функция, т.к. содержит пары с одинаковыми первыми и разными вторыми элементами, например, 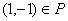 ,
,  ;
;
 - частичная функция, т.к.
- частичная функция, т.к. 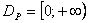 ,
, 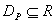 .
.

 Если задана функция f = {(x,y)|x
Если задана функция f = {(x,y)|x 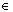 A, y
A, y 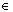 B}, то x- аргумент, y- значение функции. Различные обозначения функции: y=f(x), f: A→B, f: x→ y; A f B,
B}, то x- аргумент, y- значение функции. Различные обозначения функции: y=f(x), f: A→B, f: x→ y; A f B,
x f у. Говорят также, что f ставит в соответствие элементу х элемент у.
Пусть f = {(x,y)| x 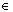 A, y
A, y 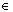 B} – функция. Она называется:
B} – функция. Она называется:
а) инъективной (инъекцией, разнозначной), если (x1,y) 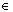 f и (x2,y)
f и (x2,y) 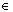 f → x1=x2 (или x1≠x2 → f(x1) ≠ f(x2)), при этом
f → x1=x2 (или x1≠x2 → f(x1) ≠ f(x2)), при этом 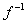 - частичная функция;
- частичная функция;
б) сюръективной (сюръекцией, отображением А на В),
если 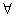 y
y  B
B  x
x  A, что (x;y)
A, что (x;y)  f, т.е. Ef = B;
f, т.е. Ef = B;
в) биективной (биекцией, взаимно-однозначным соответствием), если является и инъективной и сюръективной (для тотальной функции). Обозначается А 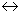 В.
В.
Заметим, что если функция частичная, то, в случае её инъективности и сюръективности, она не всегда биективна, например, 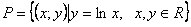 (
( 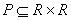 ) - частичная функция, т.к.
) - частичная функция, т.к. 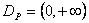 ,
, 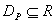 . Она инъективна, т.к. для любых
. Она инъективна, т.к. для любых 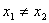 из области определения выполняется
из области определения выполняется 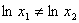 ; она сюръективна, т.к.
; она сюръективна, т.к. 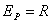 , но биекции нет, т.к. существуют
, но биекции нет, т.к. существуют 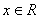 (например,
(например, 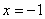 ), которым не соответствует ни один
), которым не соответствует ни один 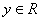 .
.
Если биекция f: А 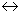 А, то она называется подстановкой множества А. Простейший пример подстановки есть тождественное отношение I.
А, то она называется подстановкой множества А. Простейший пример подстановки есть тождественное отношение I.
Пример 1.2.16 - Рассмотрим три функции  :
: 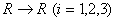 .
.
1) 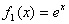 - инъективна, т.к. для любых
- инъективна, т.к. для любых 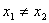 выполняется
выполняется 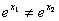 ; но не сюръективна, т.к.
; но не сюръективна, т.к. 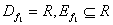 (см. рисунок 1.2.7);
(см. рисунок 1.2.7);
2) 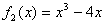 - сюръективна, т.к.
- сюръективна, т.к. 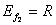 , но не инъективна, поскольку существуют
, но не инъективна, поскольку существуют 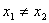 , но
, но 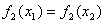 (см. рисунок 1.2.8);
(см. рисунок 1.2.8);
3) 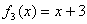 - биективна, каждому
- биективна, каждому 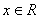 соответствует один
соответствует один  и, наоборот, (график – прямая линия).
и, наоборот, (график – прямая линия).
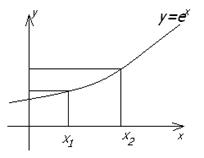
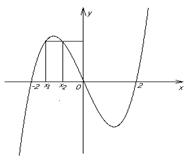
Рисунок 1.2.7 Рисунок 1.2.8
Заметим, что свойства этих, а также других функций проще всего определять по их графикам.
Пример 1.2.17 - Рассмотрим функции  :
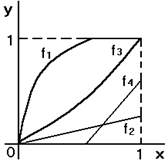
: 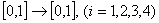 , графики которых изображены на рисунке 1.2.9:
, графики которых изображены на рисунке 1.2.9:
|
Рисунок 1.2.9
По графикам можно установить, что а) 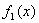 - сюръекция (не инъекция);
- сюръекция (не инъекция);
б) 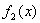 - инъекция (не сюръекция); в)
- инъекция (не сюръекция); в) 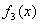 - биекция; г)
- биекция; г)  - не инъективная и не сюръективная функция.
- не инъективная и не сюръективная функция.
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 894; Нарушение авторских прав?; Мы поможем в написании вашей работы!