КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Примеры выполнения общих заданий 1 страница
|
|
|
|
Семестр
ПРИМЕРЫ ВЫПОЛНЕНИЯ УЧЕБНЫХ ЗАДАНИЙ
Указания к выполнению индивидуальных заданий
Задание 1. Обязательным индивидуальным заданием является составление конспекта урока по теме, каждый из студентов группы пишет конспект урока определенного типа: урок изучения нового материала, урок формирования умений и навыков, урок повторения. Для выполнения этого задания используйте материалы семинарских занятий по общей методике, примеры конспектов уроков студентов и учителей (журнал «Математика в школе», газета «Математика»).
Задание 2. Для выполнения задания смотрите указание для выполнения общего задания 7.
Задание 3. Для выполнения задания смотрите примеры обобщенных типов учебных задач, направленных на развитие учащихся, используя основную литературу. Пример выполнения задания смотрите на странице 71.
Задание 4. Для выполнения задания используйте литературу, предложенную к семинарским занятиям и дополнительную литературу.
Задание 5. Для показа использования компьютера при изучении темы повторите лекции и материалы семинарских занятий по общей методике по теме «Наглядность при обучении математике в школе», материалы практических занятий по информатике и методике преподавания информатики, используйте имеющиеся на кафедре компьютерные программы.
Задание 6. Для выполнения задания используйте основную, дополнительную литературу, а также литературу, предложенную к семинарским занятиям.
Задание 1
Логико-математический анализ темы: «Положительные и отрицательные числа» (выполнила студентка И. Филатова по учебнику «Математика 6», авт. Виленкин Н.Я., Жохов В.И., Чесноков А.С., М.: Мнемозина, 2009).
1. Основные математические понятия:
- положительные числа – числа со знаком «+»;
- отрицательные числа – числа со знаком «–».
- координатная прямая;
- координата точки;
- противоположные числа;
- модуль числа.
Формально-логических определений понятий «положительные числа» и «отрицательные числа» нет. Понятие «координатная прямая» определяется через ближайший род и видовое отличие.
Термин: координатная прямая.
Ближайший р од: прямая.
Видовые отличия: 1) имеет начало отсчета; 2) указано направление; 3) выбран единичный отрезок.
Все видовые отличия (свойства) в определении соединены союзом «и». Определение конъюнктивное.
2. Основные предложения темы:
– свойства противоположных чисел;
– свойства модуля числа;
– сравнение чисел;
– изменение чисел.
3. Основные идеи и методы изучения.
Результаты логико-математического анализа темы представлены в таблице 15.
Таблица 15
| Ранее изученный материал, необходимый для изучения темы | Теоретический материал темы | Применение изученного материала | |||
| – числовой луч; – изображение чисел на луче; – единичный отрезок; – сравнение положительных (натуральных и дробных) чисел. | Координата точки
Координатная прямая
Модуль числа
 Противоположные числа
Положительные и отрицательные числа Противоположные числа
Положительные и отрицательные числа
Сравнение чисел Свойства модуля числа Изменение величин | 1. Ближняя перспектива: Действия над положительными и отрицательными числами. 2. Дальняя перспектива: В курсе алгебры – при изучении графиков функций; в курсе геометрии, химии, физики. |
Теоретический материал темы изучается на наглядно-интуитивном уровне, математические методы и законы формулируются в виде правил. Используется неполная индукция, т.к. при изучении понятий и свойств не исчерпываются все частные случаи, относящиеся к данной ситуации.
Логико-математический анализ темы: «Четырехугольники»
(выполнила студентка Кошкарова М. По учебнику «Геометрия 7–9», авт. Погорелов А.В., 2010г.).
1. Основные математические понятия:
– четырехугольник – фигура, которая состоит из четырех точек и четырех последовательно соединяющих их отрезков. При этом никакие три из данных точек не должны лежать на одной прямой, а соединяющие их отрезки не должны пересекаться;
– элементы четырехугольника: вершины, стороны, соседние вершины, противолежащие вершины, диагонали, соседниестороны, противолежащие стороны;
– параллелограмм – это четырехугольник, у которого противолежащие стороны параллельны, т.е. лежат на параллельных прямых;
– прямоугольник – это параллелограмм, у которого все углы прямые;
– ромб – это параллелограмм, у которого все стороны равны;
– квадрат – это прямоугольник, у которого все стороны равны;
– средняя линия треугольника – это отрезок, соединяющий середины двух сторон треугольника;
– трапеция – четырехугольник, у которого только две противолежащие стороны параллельны. Эти параллельные стороны называются основаниями трапеции. Две другие стороны называются боковыми. Трапеция, у которой боковые стороны равны, называется равнобокой. Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.
Способы определения вновь вводимых понятий данной темы основываются на указании их характеристического свойства. Этот вид определений построен на логических действиях и операциях установления ближайшего рода, видовых отличий и логической природы связи между родом и видовыми отличиями.
Рассмотрим, например, определение параллелограмма.
Параллелограммом называется четырехугольник, у которого противоположные стороны параллельны.
Термин – параллелограмм.
Род – четырехугольник.
Видовые отличия: 1) одна пара противоположных сторон параллельна; 2) другая пара противоположных сторон параллельна.
Все свойства в определении соединены союзом “ и ”; значит, имеем конъюнктивное определение.
2. Основные предложения темы (теоремы):
Т.1. Если диагонали четырехугольника пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм.
Т. 2. (обратная Т. 1). Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
Т. 3. У параллелограмма противолежащие противоположные стороны равны, противолежащие углы равны.
Т. 4. Диагонали прямоугольника равны.
Т. 5. Диагонали ромба пересекаются под прямым углом. Диагонали ромба являются биссектрисами его углов.
Т. 6.(Фалеса) Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой стороне.
Результаты логико-математического анализа представлены в блоке В (таблица 16).
Таблица 16
Логико-математический анализ темы «Четырехугольники»
| А Ранее изученный материал, необходимый для изучения темы | В Теоретический материал темы | С Применение изученного материала |
| – треугольники, виды треугольников; – признаки равенства треугольников; – параллельность прямых; – признаки параллельности прямых; – перпендикулярность прямых. | Трапеция Ромб Квадрат Прямоугольник Параллелограмм Виды: Элементы четырехугольника ЧЕТЫРЁХУГОЛЬНИК Свойства диагоналей параллелограмма, прямоугольника, ромба. Свойства противолежащих сторон и углов параллелограмма. Свойство диагоналей прямоугольника, ромба. Теорема Фалеса. Свойства средней линии треугольника, трапеции. Теорема о пропорциональных отрезках. | 1. В теме «Многоугольники», «Площади фигур». 2. В курсе стереометрии в теме «Многогранники». 3. При изучении предметов: физика, астрономия, химия (при решении задач). 4. При решении задач в курсе геометрии, алгебры, начал анализа, а также при решении практических задач. |
Т. 7. Средняя линия треугольника, соединяющая середины двух сторон, параллельна третьей стороне и равна ее половине.
Т. 8. Средняя линия трапеции параллельна основаниям и равна их полусумме.
Т. 9. Параллельные прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки.
Задание 2
Цели изучения темы: Положительные и отрицательные числа (6 класс).
Обучающие цели:
– обеспечить усвоение понятий: положительные, отрицательные числа, противоположные числа, модуль числа, координатная прямая и правила сравнения чисел;
– научить правильно воспроизводить термины, определения понятий, приводить примеры положительных, отрицательных чисел, противоположных чисел;
– формировать умениязаписывать и читать положительные и отрицательные числа, противоположные числа, модуль числа; умения сравнивать положительные и отрицательные числа;
– формировать умения решать типовые арифметические задачи.
Развивающие цели:
– развивать познавательные процессы: внимание, восприятие, память;
– развивать мышление: умения сравнивать, обобщать, формулировать правила, алгоритмы, делать индуктивные умозаключения;
– развивать речь, мировоззрение, умение учиться.
Воспитательные цели:
– воспитывать интерес к математике и учебной деятельности через использование исторических, занимательных задач;
– воспитывать культуру общения, общую культуру;
– воспитывать отдельные качества личности (настойчивость, трудолюбие и т.д.).
Пример постановки дифференцированных учебных целей к теме «Положительные и отрицательные числа» (таблица 7) смотрите на стр. 35.
Пример постановки образовательных целей по теме «Четырехугольник и его элементы».
Обучающие цели: обеспечить в ходе урока усвоение понятия четырехугольника и его элементов; формировать умение изображать четырехугольники, обозначать элементы четырехугольников.
Развивающие цели: развивать пространственное представление, воображение, развивать умение сравнивать, формировать общеучебные умения.
Воспитательные цели: воспитывать интерес к изучению геометрии, воспитывать общую культуру.
Пример постановки дифференцированных учебных целей к темам «Положительные и отрицательные числа», «Параллелограмм» смотрите на странице 29 данного пособия (таблица 17, таблица 18).
Задание 3
Основные типы учебных задач, направленных на достижение
обучающих (учебных) целей.
На формирование знания изучаемого материала
1) Вставить пропущенные слова в формулировке определения так, чтобы оно было верным: модулем числа называется … от … до точки, которой соответствует это число.
2) Среди данных предложений выбрать правильные:
а) координатная прямая – это прямая с выбранными на ней началом отсчета и единичным отрезком;
б) два числа, отличающиеся друг от друга только знаками, называют противоположными числами;
в) любое отрицательное число больше любого положительного числа.
3) Восстановить отрывок текста: «модуль числа 6 равен …, так как точка В (…) удалена от … на … единичных отрезков. Пишут: |6| = …»
На формирование понимания изучаемого материала
1) Приведите примеры к понятию отрицательные числа; противоположные числа.
2) Запишите число, противоположное данному: – 12,7; 48; – 112; 0; 41; – 3,6.
2) Прочитайте записанные числа: -5; -0,38; 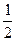 ; -
; - 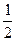 ; 0, 308.
; 0, 308.
3) Для каждой приведенной ниже записи укажите два способа ее чтения:
а) «-13» 1-й способ: «минус тринадцать»; 2-й способ: «число, противоположное тринадцати»;
б) «-7» 1-й способ: «________»; 2-й способ: «__________»;
в) «-15» 1-й способ: «_______»; 2-й способ: «__________».
Таблица 17
Дифференцированные учебные цели изучения темы «Положительные и отрицательные числа» (6 класс)
| Общие категории целей | 1 уровень | 2 уровень | 3 уровень |
| Знание | Ученик знает | ||
| Запоминание и воспроизведение изученного материала | термины: положительные числа, отрицательные, противоположные числа, модуль числа, координатная прямая; способы записи и чтения чисел, правила сравнения, частные приемы (алгоритмы) решения задач на сравнение чисел, на нахождение числа, противоположного данному, на нахождение модуля числа. модуля числа. | определения противоположных чисел, модуля числа, координатной прямой, правила сравнения, связи и отношения между определениями чисел и правилами сравнения; приемы сравнения положительных чисел, отрицательных и положительных чисел, отрицательных чисел, сравнения с нулем; обобщенные приемы решения арифметических задач на сравнение чисел, на нахождения модуля числа, контроля вычислений. | схему развития понятия числа, обоснование правил сравнения положительных и отрицательных чисел, отрицательных чисел, обобщенные приемы решения арифметических задач на сравнение чисел, на нахождение модуля числа, приемы их переноса и прикидки результата |
| Понимание | Ученик | ||
| Готовность к преобразованию изученного из одной формы в другую, к его интерпретации | правильно воспроизводит термины, формулирует правила сравнения, записывает числа, приводит примеры положительных, отрицательных чисел, записывает числа, отмеченные на координатной прямой, и наоборот. | приводит контрпримеры, подводит числа под определение, различает определение и правило, выделяет ситуации применения частных и специальных приемов сравнения чисел, нахождения противоположных чисел, нахождение модуля числа, приемы вычислений и решения задач. | преобразует словесный материал в символический и обратно: записывает числа, отмечает на координатной прямой; выводит следствия из свойств чисел, из сравнения чисел, выделяет идеи и методы рассуждения, находит новые приемы решения арифметических задач, отличающихся от типовых. |
| Умения и навыки | Ученик | ||
| Выполнение действий, составляющих прием учебной деятельности, под активным контролем внимания или автоматизированно | записывает и читает положительные и отрицательные числа, модуль числа, противоположные числа; находит модуль числа по образцу, сравнивает числа по образцу или с помощью извне, решает простейшие арифметические задачи по образцу; читает учебник и находит ответы на вопросы по тексту с помощью извне и по образцу. | решает типовые арифметические задачи, самостоятельно используя частные приемы решения задач (на нахождение противоположного числа, модуля числа, задачи на сравнение чисел); выделяет главное в учебном тексте, самостоятельно отвечает на вопросы. | решает типовые и прикладные задачи в нестандартных ситуациях, самостоятельно использует обобщенные приемы решения задач; составляет текстовые задачи по заданному числовому выражению; использует для самообразования различные источники информации |
Дифференцированные цели по теме «Параллелограмм» Таблица 18
| Учебные цели | |||
| Общие категории целей Учебные цели | 1 уровень | 2 уровень | 3 уровень |
| Знание | Ученик знает | ||
| Запоминание и воспроизведение изученного материала | термины: параллелограмм, стороны, углы, диагонали параллелограмма, символическую запись; формулировку простейших свойств параллелограмма. | определение параллелограмма, признак параллелограмма, доказательство теорем (стандарт); приемы решения задач на вычисление, доказательство, построение. | логическую структуру определения параллелограмма, общие методы доказательства (метод треугольников) и специальные методы доказательства (метод от противного). |
| Понимание | Ученик | ||
| Готовность к преобразованию изученного из одной формы в другую, к его интерпретации | правильно воспроизводит эти термины, изображает параллелограмм, его диагонали, узнает на чертеже; приводит примеры; воспроизводит форму-лировки простейших свойств, выпол- няет чертежи к простейшим задачам. | приводит контрпримеры к понятию параллелограмм; подводит объект под понятие параллелограмм; различает определение, свойства, признаки параллелограмма; выделяет частные и специальные приемы решения задач на доказательство и вычисление. | выводит следствия из определения; формулирует различные определения параллелограмма; обосновывает эквивалентность определений; проводит доказательство признаков и свойств по измененному чертежу. |
| Умения и навыки | Ученик | ||
| Выполнение действий, составляющих прием учебной деятельности, под активным контролем внимания или автоматизировано | решает простейшие (одношаговые) задачи на доказательство по образцу, используя частные приемы; для построения чертежей использует математические инструменты (линейку, циркуль, чертежный треугольник); находит ответы на вопросы в учебнике с помощью учителя. | решает типовые и прикладные задачи в стандартных ситуациях, используя алгоритмы и частные приемы; выделяет главное в учебном тексте. | решает типовые и прикладные задачи в нестандартных ситуациях; составляет задачи по чертежу; проводит этап исследования задачи. |
| Развивающие цели | |||
| Представление и воображение | Ученик | ||
| Отражение изучаемых и создание новых образов и объектов | после объяснения узнает признаки и свойства параллелограмма по рисункам и кратким записям | самостоятельно воспроизводит рисунок параллелограмма, краткую запись. Может сформулировать определение, признаки, свойства | создает образ параллелограмма точно и четко в измененных ситуациях. |
Продолжение таблицы 18
| Мышление | Ученик | ||
| Сравнение Установление сходства и различия объектов по каким-либо признакам | Выявляет общие и различные, существенные и несущественные свойства параллелограмма. Выделяет параллелограмм среди других четырехугольников | Осознает структуру сравнения, устанавливает сходство и различие четырехугольников по параллельности противолежащих сторон | Находит различные основания для сравнения параллелограмма и произвольного четырехугольника, параллелограмма и прямоугольника |
| Оперирование понятиями Формулировка определений, сравнение и классификация, установление отношений между понятиями | Узнает и правильно воспроизводит определение параллелограмма, выделяет в нем составные части (термин, родовое понятие, видовые отличия) | Отличает определение парал-лелограмма от других предложений (свойств и признаков), знает прием определения понятия через ближайший род и видовое отличие, выполняет подведение под понятие «парал-лелограмм», используя определение | Выводит следствие из определения параллелограмма, используя признаки параллелограмма, формулирует другие определения параллелограмма, доказывает их равносильность |
| Речь | Ученик | ||
| Межличностное общение посредством языка устно или письменно | правильно произносит термины (параллелограмм, диагонали, стороны и т.п.), формулирует признаки и свойства параллелограмма (не всегда точно), делает записи в тетради и отвечает на вопросы по образцу или с помощью. | формулирует определение, признаки и свойства параллелограмма, используя специальные приемы (формулирует теоремы в категоричной или условной форме), строит рассказ, делает записи в тетради самостоятельно, свободно задает и отвечает на вопросы. | разъясняет ход доказательства свойств и признаков параллелограмма или решения задач на их использование с использованием специальной терминологии (если …, то …; из … следует… и др.). Ведет специальную дискуссию, внимательно слушает речь других, оценивает правильность речи. |
| Воспитательные цели | |||
| Познавательный интерес | Ученик проявляет интерес | ||
| случайный, непосредственный к конкретным фигурам, имеющим форму параллелограмма | настойчивый, осознанный, избирательный к изучению параллелограмма, свойствам и признакам | к способам доказательства свойств и признаков, к формулировкам различных определений параллелограмма, к доказательствам их равносильности, в их применении | |
| Нравственные качества личности | Ученик проявляет | ||
| нравственные знания, положительное отношение к учащимся, принимает ценностные ориентации извне. | нравственное поведение и готовность к помощи в самовоспитании, предпочтение ценностных ориентаций, инициативы. | проявляет стремление осознать способы самовоспитания, проектирование своей личности, самостоятельность позиции и убежденность |
На формирование умений и навыков
1) Запишите координаты отмеченных на прямой точек.
0 1
 ● ● ● ● ● ●
● ● ● ● ● ●
D В А С
2) Укажите стрелкой положительное направление на каждой из прямых:


 ● ● ● ● ● ●
● ● ● ● ● ●
–1 0 – 3 –1 1 0
3) Заполните пустые места в таблице и отметьте все числа, представленные в таблице, на числовой прямой.
Таблица 19
| Х | –7 | |||||
| – Х | –3 |
Типы учебных задач, направленных на достижение развивающих целей
На развитие внимания
1) расположите в порядке возрастания числа: – 0,3; – 4,8; – 2,5; – 0,8; 5;
2) какие целые числа заключены между числами: – 1,2 и 3,54; – 4,7 и 2,1
на развитие восприятия
1) сравните два числа: – 0,34 и – 0,304;
2) выслушайте и запишите (изобразите на координатной прямой) продиктованные числа: – 5,5; – 2; 2; 4,5; – 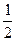 .
.
На развитие памяти
1) Посмотрите минуту на данные числа, затем по памяти запишите их в том же порядке: – 5,8; – 2,6; 4,5; – 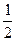 ; 0; – 4.
; 0; – 4.
2) Назовите термины данной темы, начинающиеся на букву «к», «м».
На развитие мировоззрения
1) Приведите примеры объектов, явлений реальной действительности, описываемых с помощью отрицательных и положительных чисел (например, температура воздуха, долг и прибыль, высота над уровнем Мирового океана и т.п.).
Типы учебных задач для достижения воспитательных целей
На воспитание интереса к математике
1) Решите занимательную задачу: отметьте на «линии времени» следующие события из истории математики:
а) книга «Начала» была написана Евклидом в III в. до н. э.
б) теория чисел зародилась в Древней Греции в VI в. до н. э.
в) десятичные дроби появились в Китае в III в.
г) теория отношений и пропорций была разработана в Древней Греции в IV в. до н.э.
д) позиционная десятичная счисления распространилась в странах Востока в IX в.
Сколько веков назад произошли эти события? Сравните «линию времени» и координатную прямую;
2) Решите математический кроссворд.
На воспитание культуры общения
1) Объясните партнеру по группе задание (указать задание по теме);
2) Проверьте у партнера по группе выполнение задания, помочь его выполнить.
Задание 4
Мотивация изучения понятия «квадратное уравнение»
Для того чтобы учащиеся увидели, что при решении задач из различных областей действительности им понадобятся знания о квадратных уравнениях и способах их решения, работу по изучению понятия можно начать с рассмотрения таких задач:
1) Задача № 559 из учебника «Алгебра 8» под ред. С.А. Теляковского. – М.: Просвещение, 2009. – 239 с.
2) После двух повышений цен на одинаковое число процентов цена 1 м ткани повысилась с 27 рублей до 34 рублей. На сколько процентов повышалась каждый раз цена 1 м ткани и на сколько процентов за все это время повысилась цена ткани?
Одна из них, например № 559, решается со всем классом, и в результате учащиеся получают уравнение  , где х м – ширина огородного участка. Способ решения полученного уравнения учащимся неизвестен. Такие уравнения они еще не решали. Чтобы научиться решать такие уравнения необходимо изучить уравнения такого вида.
, где х м – ширина огородного участка. Способ решения полученного уравнения учащимся неизвестен. Такие уравнения они еще не решали. Чтобы научиться решать такие уравнения необходимо изучить уравнения такого вида.
Этап мотивации завершается постановкой учителем учебной задачи: выявить существенные признаки нового вида уравнений, сформулировать определение нового вида уравнений и найти способы их решения.
Задание 5
Методика введения понятия «четырехугольник»
(фрагмент урока по теме «Четырехугольник и его элементы» по учебнику «Геометрия 7–9», авт. А.В.Погорелов, 2009 г. Составила студентка Шляпова Н.)
Тип урока: изучение нового материала.
Обучающая цель: ввести понятие четырехугольника и его элементов.
Вид доски на начало урока
1) 2) 3)
4) 5) 6)
7) Рис. 1 | Рис. 2 Рис. 3 |
Таблица 20
| Деятельность учителя. | Деятельность учащихся |
| Актуализация опорных знаний (диалог): 1) Назовите, под каким номером на рис. 1 изображены треугольники? Дайте определение треугольника. 2) Назовите элементы треугольника. Введение понятия (диалог): 3) Что объединяет фигуры под номерами 2, 4, 5, 6, 7 на рис.1? 4) Сформулируйте определение четырехугольника по аналогии с определением треугольника. 5) Является ли четырехугольником фигура на рис. 2? 6) Является ли четырехугольником фигура на рис. 3? 7) Значит, данное вами определение четырехугольника надо дополнить. Как надо соединять точки отрезками? 8) Попробуйте сформулировать определение четырехугольника, учитывая последний вывод. 9) Данные точки называются вершинами четырехугольника, а отрезки сторонами. Усвоение понятия (самостоятельная работа с учебником) 1) Прочитайте п. 50 на стр. 81 (до задачи). 2) Рассмотрите рисунки в учебнике на стр. 81. Являются ли данные фигуры четырехугольниками? Какое условие определения не выполняется? 3) Приведите пример четырехугольника, начертите в тетради, обозначьте его вершины, выпишите название четырехугольника, вершины, стороны. 4) Какие виды четырехугольников вы знаете? | – Треугольники изображены под номером 1 и 3. – Треугольником называется фигура, которая состоит из трех точек, не лежащих на одной прямой и трех попарно соединяющих их отрезков. – Вершины и стороны. – Фигуры под номерами 2, 4, 5, 6, 7 состоят из 4 точек и 4 отрезков, соединяющих эти точки, и 4 углов. – Четырехугольником называется фигура, которая состоит из четырех точек, не лежащих на одной прямой и четырех попарно соединяющих их отрезков. – Нет, на рис. 2 изображен треугольник, т.к. одна из четырех точек лежит на отрезке, соединяющем две другие точки. – Нет, т.к. соединяющие отрезки пересекаются. – Точки надо соединять последовательно. – Четырехугольником называется фигура, которая состоит из четырех точек, никакие три из которых не лежат на одной прямой и четырех последовательно соединяющих их отрезков. Термин – четырехугольник; Род – фигура; Видовые отличия – состоит из четырех точек и четырех последовательно соединяющих их отрезков и никакие из трех точек не лежат на одной прямой. (логическая структура определения) Читают. – Не являются. На рис. 88 точки B, C, D находятся на одной прямой. На рис. 89 отрезки DB и CA пересекаются. – ABCD – четырехугольник, А, В, С, D – вершины четырехугольника, АВ, ВС, СD, AD – стороны четырехугольника. Прямоугольник, квадрат. |
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 3786; Нарушение авторских прав?; Мы поможем в написании вашей работы!