Примеры выполнения общих заданий 2 страница

Задание 6

Методика изучения теоремы «Сумма углов треугольника» (7 класс)

(фрагмент урока по теме «Сумма углов треугольника» по учебнику «Геометрия 7–9», автор Погорелов А.В., 2009 г.)

Тип урока: Урок изучения нового материала.

Обучающая цель: Обеспечить усвоение теоремы о сумме углов треугольника.

Мотивация изучения теоремы «Сумма углов треугольника»

Учащимся предлагается решить следующую задачу: дан треугольник АВС, два угла которого известны. Найти третий его угол.

На этапе поиска идеи решения задачи отмечается, что она может быть решена при условии, что сумма всех углов любого треугольника величина постоянная. Для решения задачи необходимо знать эту величину.

Этап мотивации заключается постановкой учебной задачи: определить, чему равна сумма углов произвольного треугольника.

Таблица 21

Деятельность учителя

Деятельность учащихся

1. Подготовительный этап. Практическая работа. Предлагаю учащимся задание: построить треугольники. 1 вариант: треугольник АВС, угол А=43⁰, угол В=37⁰. 2 вариант: треугольник MNK, угол М=54⁰, угол N=76⁰. 3 вариант: треугольник LPE, угол L=65⁰, угол Р=25⁰. После построения измерить третий угол, найти сумму углов треугольника, установить вид треугольника. Задаю вопросы: - назовите чему равна сумма углов в остроугольном треугольнике; тупоугольном; прямоугольном? - зависит ли сумма углов треугольника от вида треугольника? Результаты работы позволяют высказать гипотезу о том, что сумма углов треугольника равна 180 ⁰. Мотивация необходимости доказательства теоремы. Как вы уже знаете, нельзя выполнить ни абсолютно точных построений, ни произвести абсолютно точного измерения. Поэтому правильнее было бы сказать: рассмотренные нами треугольники имеют сумму углов приблизительно равную 180 ⁰ . Но такое утверждение относится только к рассмотренным нами треугольником. - Можем ли мы сказать это и о других треугольниках? Работа над структурой теоремы Предлагаю ответить на следующие вопросы:     1) какие треугольники использовались в процессе проведения измерений? 2) Что входит в условие теоремы? 3) Что мы обнаружили при измерении? 4) 5) В чем состоит заключение теоремы? 6) Попробуйте сформулировать теорему о сумме углов треугольника.

А

Основной этап

Построение чертежа и краткая запись

теоремы

Предлагаю учащимся сделать рисунок и записать, что дано и что требуется доказать.

Поиск доказательства теоремы

Чтобы доказать теорему, развернем заключение (анализ).

- В каких утверждениях говорится об углах, сумма величин которых равна 180⁰?

- Попробуем для доказательства использовать первое утверждение. Для этого необходимо сделать дополнительное построение: провести параллельные прямые и секущую. Как это можно сделать?

- Проведем прямую через вершину В параллельную АС.

- Назовите образовавшиеся при этих прямых и секущей внутренние односторонние угла.

- Сумма каких углов будет равна 180⁰?

-Что можно сказать о величине угла ABD?

- Какого утверждения нам не хватает, чтобы доказать теорему?

- Какие это углы и можем ли мы сказать, что они равны?

В результате поиска доказательства

составляем план доказательства

1) Через одну из вершин треугольника провести прямую параллельную противолежащей стороне;

2) Доказать равенство внутренних накрест лежащих углов;

3) Записать сумму внутренних односторонних углов и выразить ее через углы треугольника.

Доказательство и его запись

Работа над доказательством и его оформление проводится в ходе беседы с классом, в соответствии с ранее составленным планом. Доказательство записывается на доске учителем и в тетрадях учащимися.

Усвоение теоремы

Закрепление формулировки теоремы и ее доказательства

Для усвоения формулировки теоремы предлагаю выполнить учебные задания:

а) сформулируйте теорему;

б) выделите условие и заключение теоремы;

в) к каким фигурам применима теорема?;

г) сформулируйте теорему со словами «если…, то…»;

д) из предложенных формулировок теорем выберите истинные:

«В треугольнике углы равны 180⁰»

«Сумма углов равна 180⁰»

«Если дан треугольник, то сумма его углов равна 180⁰»

«В прямоугольнике сумма углов равна 180⁰»

«В треугольнике сумма равна 180⁰».

Для усвоения доказательства предлагаю вопросы:

1. На основании какого утверждения мы можем провести прямую ВD параллельную АС?

2. Почему углы DBC и АСВ – внутренние накрест лежащие, а углы ВАС и АВD – внутренние односторонние для прямых АС и ВD и секущей ВС?

3. На основании чего можем утверждать, что ВС- нутренний луч угла АВD?

4. Предлагаю доказать теорему по измененному чертежу: провести прямую СD параллельную АВ.

5. Для усвоения доказательства предлагаю карточки: заполнить пропуски.

Применение теоремы

1. Предлагаю решить задачи, которые являлись средством постановки проблемы для конкретных значений двух углов.

2. Могут ли два угла треугольника быть одновременно тупыми? Прямыми?

3. Может ли один из углов быть прямым, а другой тупым?

4. Какой вывод можно сделать о том, какие углы могут быть в треугольнике.

Предлагаю задания, для выполнения которых наряду с теоремой о сумме углов треугольника используется ранее изученный материал:

1) Найдите углы равностороннего треугольника.

2) Найдите углы, если известно их отношение.

3) Найдите углы равнобедренного треугольника, если известен один из углов.

    Учащиеся выполняют построение в тетради; выполняют необходимые вычисления. 1 вариант: тупоугольный треугольник. 2 вариант: остроугольный треугольник. 3 вариант: прямоугольный треугольник.     – сумма углов равна 180⁰ (или приблизительно равна 180⁰).   – сумма углов треугольника не зависит от вида треугольника и равна 180⁰.   - - - - - - - - - Нет, не можем, так как их углы не измеряли. Чтобы убедить в том, что сумма углов треугольника точно равна 180 ⁰ и при том для любых треугольников, нам нужно еще провести соответствующие рассуждения, т.е. доказать справедливость утверждения, подсказанного нам опытом. - -остроугольный, прямоугольный и тупоугольный; - -Нам дан треугольник. Произвольный. - -Сумма углов равна приблизительно 180⁰. - -Сумма углов треугольника равна 180⁰. Сумма углов треугольника равна 180 ⁰ .   В D Дано: ∆АВС. .     С Доказать: ÐА + ÐВ+ÐС=180⁰   - Если две параллельные прямые пересечены третьей прямой, то сумма внутренних односторонних углов равна 180⁰. - Сумма смежных углов равна 180⁰.     - Через одну из вершин треугольника провести прямую, параллельную другой стороне, тогда одна из боковых сторон будет секущей.   - Углы DBA и BAC.     - Углов DBA и BAC. - Его величина равна сумме углов ABC и CBD. - Что Ð DBC = ÐACB. - Это внутренние накрест лежащие углы, по свойству внутренних накрест лежащих углов мы можем сказать, что они равны. Доказательство: 1. Дополнительное построение: BDIIAC. 2. D и A по разные стороны от прямой BC, углы DBC и ACB – внутренние накрест лежащие при прямых АС и BD и секущей ВС (по определению). 3. ÐDBC= ÐACB=ÐС (по свойству внутренних накрест лежащих углов при параллельных прямых и секущей). 4. ÐABD= ÐABC + ÐCBD = ÐВ + ÐCBD (ВС – внутренний луч угла ABD). 5. ÐABD= ÐВ + ÐС (утверждения 3 и 4). 6. Ð ВАС и ÐАВD – внутренние односторонние углы при параллельных прямых ВD и АС и секущей ВС (по определению внутренних односторонних углов). 7. ÐВАС + ÐАВD = 180⁰ (по свойству внутренних односторонних углов). 8. ÐА+ÐВ+ÐС=180⁰ (утверждения 5 и 7). Ч.т.д.   Отвечают на вопросы, обосновывают ответ.   - На основании аксиомы параллельных.   - По определению этих углов (формулируют определения).   - На основании построения и определения.   Утверждения Обоснования (смотри доказательство)   А= 43⁰, В=56⁰. Найти угол С. С= 180⁰ – (43⁰ + 56⁰)= 81⁰. - Нет, так как в этом случае сумма углов будет больше 180⁰. - Нет, так как сумма углов также будет больше 180⁰. - У любого треугольника хотя бы два угла острые.     Решают у доски, оформляют решение.

Задание 7

Основные типы математических задач по теме «У равнения» (7 класс)

– решить линейное уравнение первой степени с одним неизвестным;

– решить задачу методом составления уравнения первой степени с одним неизвестным.

Обобщенный прием решения уравнений с одной переменной (ax=b)

1) определить, является ли уравнение линейным, если «да», то п.4, если «нет», то п.2;

2) установить, какое из следующих тождественных и равносильных преобразований нужно выполнить, чтобы привести уравнение к линейному: раскрытие скобок, приведение к общему знаменателю, перенесение членов из одной части в другую, приведение подобных;

3) привести с помощью выбранных преобразований уравнение к линейному ax=b;

4) найти x= 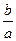при а 0;

5) если нужно, сделать проверку, исследование;

6) записать ответ (если нужно, изобразить его на числовой оси).

Задание 8

Решить математическую задачу

Задача. Упростить выражение

Решение:

1) Изучение содержания задачи. Данное выражение представляет собой частное от деления разности двух дробей на дробь, это дробное рациональное выражение, определенное на множестве всех рациональных чисел, кроме тех, которые обращают знаменатель в ноль. Область допустимых значений удобнее найти в процессе решения.

2) Поиск решения задачи (анализ). Чтобы упростить это выражение, надо выполнить вычитание дробей и деление результата вычитания на дробь, применяя соответствующие правила действий с дробями. Деление можно заменить умножением на дробь, обратную данной (делителю), предварительно упростив знаменатель. Из правил действий с дробями следует, что разность, частное и произведение рациональных дробей всегда можно представить в виде рациональной дроби. Значит, и все рациональное выражение можно представить в виде рациональной дроби.

3) План решения задачи.

– определить порядок выполнения действий: сначала выполнить вычитание дробей, заключенных в скобки, полученный результат умножить на дробь, обратную данной;

– выполнить действия с дробями, соблюдая соответствующие правила и приемы;

– записать ответ.

4) Решить задачу по составленному плану, з аписать решение, используя приемы записи. Запись можно вести:

а) последовательно в виде «цепочки»:

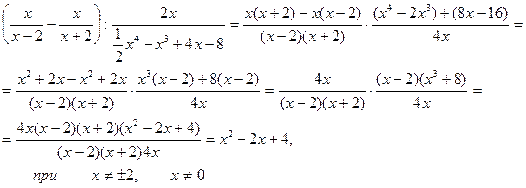
б) параллельно, по действиям:

1)

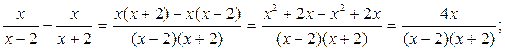
2)

3)

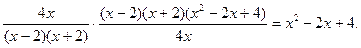
5) Проверка и исследование решения состоит в проверке правильности выполнения каждого шага, в правильности применения правил действий с дробями (вычитание, деление, сокращение дробей).

Исследование состоит в выяснении вопроса: всегда ли задача имеет решение. Так как дробное выражение при некоторых значениях переменных может не иметь смысла, то необходимо найти допустимые значения переменных. В нашей задаче выражение имеет смысл при тех значениях х, при которых знаменатель не равен нулю, т.е.

6) Записать ответ. Ответ: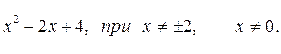

7) Анализ решения задачи. Решение задачи полностью соответствует приему решения задач данного типа.

Задание 9

Методика обучения решению текстовых задач методом составления

рациональных уравнений (8 класс)

Задача. Из города в село, находящееся от него на расстоянии 120 км, выехали одновременно два автомобиля. Скорость одного была на 20 км/ч больше скорости другого, а поэтому он пришел к месту назначения на 1 ч раньше. Найдите скорость каждого автомобиля.

1) Изучение содержания задачи.

Краткая запись содержания задачи:

Таблица 22

Величины	Ситуации
1 автомобиль	2 автомобиль
Расстояние, км
Скорость, км/ч	? >?	На 20
Время, ч	? <?	На 1

Задача текстовая, на движение, описаны две ситуации: из города в село выехали два автомобиля. Основные величины: расстояние (км), скорость (км/ч), время (ч), основное отношение (связь между величинами): S=vt. Известные величины – расстояние между городом и селом 120 км, скорость одного велосипедиста на 20 км/ч больше скорости другого, а время движения на 1 ч меньше. Искомые величины – скорости каждого автомобиля.

2) Поиск решения задачи.

Введем обозначение одной из искомой величин: пусть х км/ч - скорость 2-го автомобиля. Заполним таблицу поиска решения задачи:

Таблица 23

Величины	Ситуации
1 автомобиль	2 автомобиль
Расстояние, км
Скорость, км/ч	х +20 > х	На 20
Время, ч	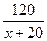<	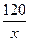На 1

Исходя из таблицы 23 (модели поиска решения), выписываем условие 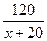< 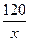на 1, с помощью которого составляем уравнение 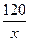– 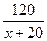=1 (модель задачи).

3) Решение задачи и оформление решения (решение модели).

Для решения используем общий прием решения математической задачи, смотрите образец выполнения задания 8.

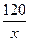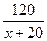- =1, общий знаменатель дробей: х (х +20)

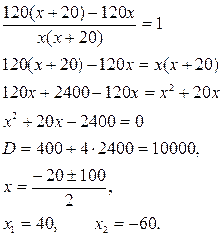
4) Проверка и исследование решения задачи. По условию задачи х – скорость автомобиля величина положительная, корень уравнения х = – 60 не удовлетворяет условию задачи (проверка по смыслу задачи).

Проверим, удовлетворяет ли условию и требованию задачи корень уравнения х =40.

Первый способ (используем модель поиска): Пусть 40 км/ч скорость 2-го автомобиля, тогда 60 км/ч скорость 1-го автомобиля, 120:40=3 (ч) время движения 2-го автомобиля, 120:60=2 (ч) время движения 1-го автомобиля; 3–2=1 (ч), на столько раньше прибыл в путь назначения 1-й автомобиль, что соответствует условию задачи. Следовательно, х =40 (км/ч) является решением задачи. Скорость 1-го автомобиля 60 км/ч.

Второй способ письменного оформления проверки корней уравнения по смыслу задачи состоит в следующем: совместно с уравнением, составленным по тексту задачи, рассматриваются смысловые ограничения для значений величин, входящих в задачу. Получают систему: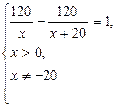

Исследование задачи: так как уравнение 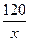– 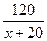=1 дробное рациональное уравнение, то найдем область определения уравнения. Уравнение определено на множестве всех рациональных чисел, кроме х =0 и х = – 20.

5) Ответ: скорость 1-го автомобиля 60 км/ч, скорость 2-го автомобиля 40 км/ч.

6 ) Изучение (анализ) найденного решения. Данная задача решена алгебраическим методом, методом составления уравнения. Решение задачи полностью соответствует приему решения задач такого типа. Данную задачу можно решить также выбрав в качестве неизвестного скорость 1-го автомобиля или время движения 1-го или 2-го автомобиля. Наиболее рациональным является данное решение.

Учебные задачи на формирование умения изучать содержание задачи

1. Прочитать задачу:

Задача 1. Теплоход «Метеор» за час проходить расстояние в 5 раз большее, чем катер. Сколько километров в час проходит каждый из них, если сумма их скоростей равна 90 км/ч?

2. Описать ситуации, заданные в задаче 1 (о чем идет речь в задаче). Установить тип задачи.

3. Назвать величины, рассматриваемые в задаче 1.

4. Записать зависимость между величинами в виде формулы к задаче 1.

5. Назвать величины (задача 1), которые связаны зависимостью: одна больше другой в 5 раз.

6. Если катер проходит х км/ч, то как можно истолковать выражения: 5 х, 5 х + х? Значение какой из представленных здесь величин известно по условию задачи 1?

7. Используя справочный материал, заполнить пропуски в тексте задачи 2.

Задача 2. Футбольная команда школьников выиграла на … состязаний …, чем проиграла. Число проигранных состязаний в … числа состязаний, проведенных вничью. Сколько проведено состязаний, если ничьих было на …, чем проигрышей?

Справочный материал: команда школьников выиграла 16 состязаний, проиграла 6 и свела вничью 2 состязания.

8. Не решая задачи 3, составить краткую запись а) в виде таблицы; б) в виде графической схемы.

Задача 3. Площадь, засеянная овсом и рожью 60 га. Какова площадь, занятая каждой культурой, если ржи собрали на 440 ц больше, чем овса, снимая с каждого га по 26 ц, а урожайность овса 30 ц с 1 га?

9. По краткой записи составить задачу:

Таблица 24

Величины	Ситуации
1 велосипедист	2 велосипедист
Скорость, км/ч	<	На 3
Время, ч
Расстояние, км	+	=76

Учебные задачи на формирование умения осуществлять поиск решения задачи

1. Используя таблицу 10, выбрать за неизвестное скорость 1-го велосипедиста (х км/ч) и заполнить таблицу. Записать полученное уравнение.

2. Используя таблицу 10, выбрать за неизвестное расстояние, пройденное 1-м велосипедистом (х км) и заполнить таблицу. Записать полученное уравнение.

3. Дополнить приведенные ниже выражения до уравнения, к которому сводится решение задачи 5: а) 9 х +…=180; б) 180…=6 х; в) …9 х =….

Задача 4. С противоположных концов катка длиной 180 м бегут навстречу друг другу два мальчика. Через сколько секунд они встретятся, если начнут бег одновременно и если один пробегает 9 м/с, а другой 6 м/с?

4. Заполнить пропуски в анализе задачи.

Задача 5. Моторная лодка прошла 25 км по течению реки и 3 км против течения, затратив на весь путь 2 ч. Какова скорость лодки в стоячей воде, если скорость течения реки 3 км/ч?

Анализ: пусть х км/ч – скорость лодки в стоячей воде, тогда скорость лодки по течению реки … км/ч. По течению реки … км лодка прошла за …ч, а против течения … км за … ч. Значит, время, затраченное на весь путь равно … ч.

По условию задачи на весь путь лодка затратила … ч, следовательно, можно составить и решить уравнение ….

Учебные задачи на формирование умения решать уравнение

(модель задачи) и на формирование умения оформлять решение

1. Определить виды уравнений: 10х+54=7(х+27); ; .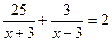

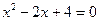2. Сформулировать прием решения уравнений перечисленных выше.

3. Найти корни уравнения .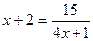

4. Не решая уравнение определить, имеют ли уравнения корни:

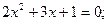
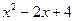=0.

5. Решив уравнение 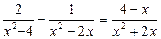, ученик записал ответ: корни уравнения 2; 3. Верно ли это?

Учебные задачи на формирование умения проверять и исследовать решение задачи

1. Решая задачу «Моторная лодка прошла 25 км по течению реки и 3 км против течения, затратив на весь путь 2 ч. Какова скорость лодки в стоячей воде, если скорость течения реки 3 км/ч?», ученик получил уравнение, корни которого 2 и 12. Какой из корней удовлетворяет условию задачи и почему?

2. Проверить правильность решения уравнений, составленных по тексту задачи (смотрите пример выполнения задания 8).

Учебные задачи на формирование умения анализировать решение задачи

1. Сформулировать общий прием решения задач методом составления уравнения.

2. Дана задача.

Задача 6. Один из лыжников прошел расстояние в 20 км на 20 минут быстрее, чем другой. Найдите скорость каждого лыжника, зная, что один из них двигался со скоростью, на 2 км/ч большей?

а) Решить задачу, выбрав за неизвестное х скорость 1-го лыжника (для определенности, скорость которого больше).

б) Решить задачу, выбрав за х скорость 2-го лыжника.

в) Решить задачу, выбрав за х время движения 1-го лыжника? 2-го лыжника?

г) Сравнить результаты решения, выбрать наиболее рациональное решение.

д) Составить и решить обратную задачу.

е) Составить и решить аналогичную задачу.

Методика обучения решению геометрических задач на вычисление

Задача. Основание равнобедренного треугольника равно а, угол при противоположной вершине 2a. Найти биссектрису, проведенную к боковой стороне.

Решение задачи смотрите на странице 39.

Учебные задачи на формирование умения изучать содержание задачи

1. Выделите основной объект задачи (какая фигура рассматривается в задаче).

2. Выведите следствия из того, что треугольник равнобедренный.

3. Изобразите равнобедренный треугольник. Обозначьте его.

4. Выведите следствия из того, что луч АС является биссектрисой угла.

5. Один из углов равнобедренного треугольника равен α, что можно сказать о двух других углах? Рассмотрите возможные случаи.

6. Отметьте данные задачи на чертеже.

7. Какие из известных элементов фигуры не отмечены на чертеже?

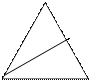В

К

А С Рис. 3.

8. Составьте краткую запись задачи: Дано: Найти;

9. По приведенным кратким записям сформулируйте соответствующие им задачи:

а) Дано: ∆АВС, ÐА=ÐВ, б) Дано: ∆АВС, АВ=АС, ÐА=70⁰,

АВ= 12см, ÐС = 80⁰. АС=8см, ÐАВК =ÐКВС, КÎАС.

Найти: АС. Найти: ВК.

10. Проведите анализ задачи, используя схему: 1) объект задачи; 2) данные элементы; 3) искомые элементы; 4) заданные соотношения.

Учебные задачи на формирование умения осуществлять поиск решения задачи

1. В равнобедренном ∆ АВС основание АС=10 см. Найти среднюю линию треугольника.

2. Запишите формулу, по которой можно найти искомую величину.

3. В равнобедренном ∆МКL проведена биссектриса угла М – МЕ. Перечислите треугольники, в который входит отрезок МЕ. Рассмотрите возможные случаи.

4. Проведите поиск решения данной задачи, используя восходящий анализ и заполняя пропуски в тексте: Чтобы найти …, надо рассмотреть треугольники, в которые входит искомый отрезок…. 1) треугольник…, в котором известна сторона… и 2) треугольник…, в котором известен угол…. Так как треугольник … равнобедренный и отрезок … биссектриса, то угол… равен углу…. и равен ½ угла…. Применяя теорему синусов к треугольнику…, можно найти искомый отрезок….

5. В равнобедренном треугольнике сумма двух углов равна 2α.Найти все углы треугольника. Рассмотреть возможные случаи.

6. В треугольнике АВС известны два угла α и β и сторона а. Записать теорему синусов для этого треугольника и найти сторону в.

Учебные задачи на формирование умения оформлять решение

1. Определить вид задачи:

Задача 1. В треугольнике сумма двух сторон равна 14 см, а третья сторона делится биссектрисой противоположного угла на отрезки 3 см и 4 см. Найдите стороны треугольника.

Задача 2. В прямоугольном треугольнике АВС из вершины С прямого угла проведены биссектриса СК и медиана СМ. Найти катеты треугольника АВС, если КМ = а, СМ = m.

Задача 3. Периметр равнобедренного прямоугольного треугольника с гипотенузой 15см равен 36 см. Чему равна площадь этого треугольника?

2. Для задачи 3 заполнить пропуски в решении:

Решение: S= …, где а и в катеты.

1) а=в, т.к. …; а=в=…;

2) S= ….

Ответ:…

3. Для задачи 1 составить модель задачи, обозначив за х одну из сторон; решить полученное уравнение; записать ответ на вопрос задачи.

4. Задача 4. Найдите стороны равнобедренного треугольника АВС, если ÐА = 75⁰, а высота АК= 3м. Заполните пропуски в решении задачи.

Решение (прием оформления решения: обоснование – действие):

1) Треугольник АВС равнобедренный (по условию), отсюда следует, что… ÐВ=ÐС=…

2) Треугольник АВК – прямоугольный (по условию АК - …), отсюда по… следует, что АВ=…; ВК=…., АС=…

3) АК - высота (по условию), проведенная к основанию равнобедренного треугольника, отсюда следует, что АК -… и ВС=….

Решение (прием оформления решения: действие - обоснование):

1) Из ∆ АВС ÐВ=ÐС=…, так как…;

2) Из ∆ АВК АВ =…, ВК =…, так как…; и по …; АС =… по….

3) ВС = …., так как АК – высота …и …

Учебные задачи на формирование умения проверять и исследовать задачи

1. Составить задачу, обратную задаче 3.

2. При решении задачи 4 ученик обозначил угол А при основании равнобедренного треугольника и решил задачу. Найдите ошибку.

3. При решении задачи 4 ученик нашел, что АВ = АК соs А. Верно ли это?

4. При каких значениях а и m имеет решение задача 2.

5. Один из углов равнобедренного треугольника равен 80⁰, какой это угол?

Учебные задачи на формирования умения анализировать решение задачи

1. Сформулировать общий прием решения геометрической задачи на вычисление.

2. Сформулировать прием решения геометрической задачи на вычисление методом составления уравнения (алгебраическим методом).

3. Дана задача.

Задача 5. В равнобедренном треугольнике один из углов равен 50⁰, основание треугольника равно 8 см. Найти биссектрису данного угла.

1) Решить задачу арифметическим и алгебраическим способом а) дан угол при вершине равнобедренного треугольника; б) дан угол при основании равнобедренного треугольника.

2) Сравнить результаты решения для случая а); выбрать наиболее рациональное решение.

3) Составить и решить обратную задачу.

4) Составить и решить аналогичную задачу.

Задание 9

Организация коррекционной работы по теме «Площади фигур»

Дата добавления: 2014-12-27