Параллельность прямых и плоскостей в пространстве

Примеры выполнения индивидуальных учебных заданий

Тематический план для образовательных классов (фрагмент)

№ урока дата	Содержание учебного материала	Кол-во часов	Повторение	Оборудование урока	Основные математические понятия
2, 3	Двугранный угол Трехгранный и многогранные углы	3ч.	Т. Пифагора Т. косинусов Параллельный перенос Построение угла между плоскостями	Цветной мел Модель куба	Двугранный угол, грани, ребро, линейный угол трехгранный угол
4. 5.	Многогранники Призма Изображение призмы Построение сечений призмы Правильная и прямая призма Полная поверхность призмы	3 ч.	Признаки параллельности и перпендикулярности прямых и плоскостей Параллельный перенос Площади треугольника	Модели многогранников Призмы Кодо- позитивы Слайды (см. с.)	Многогранник его элементы призма элементы призмы: высота, диагональ, перпендикулярное сечение Прямая, правильная призма
6.	Теорема о боковой поверхности призмы Решение задач		прямо- угольника параллелограмма трапеции		Боковая поверхность Полная поверхность
7. 8. 9.	Центральная Параллелепипед симметрия параллелепипеда Прямоугольный параллелепипед Теорема о его диагонали Решение задач	1 ч. 2ч.	Определение параллелограмма Свойства Признаки	Модели параллелепипеда	Параллеле-пипед прямой и наклонный Прямоуго-льный
10. 11.	Решение задач Контрольная работа	1 ч. 1ч.		кодопозитивы

(10 класс, учебник «Геометрия 10–11», авт. Погорелов А.В.)

(Пример выполнения задания на II уровне приведен в таблице 14)

Учебные задачи, направленные на достижение учебных целей

по теме «Параллельность прямых и плоскостей»

– две прямые в пространстве называются параллельными, если …;

– две прямые в пространстве называются скрещивающимися, если …

2. Приведите примеры объектов (из интерьера комнаты), которые можно считать реальными параллельными прямыми (отрезками), перечислите их;

– могут ли две параллельные прямые лежать в разных плоскостях (ответ поясните)?

– могут ли пересечься две скрещивающие прямые (ответ поясните)?

– верно ли утверждение, что две прямые, каждая из которых скрещивается с третьей прямой, скрещиваются между собой?

№	Общие категории целей	Примеры обобщенных типов целей
I уровень	II уровень	III уровень
1.	Знание	Ученик знает
	Запоминание и воспроизведение изученного материала	термины, обозначения, правила и алгоритмы изображения параллельных прямых и плоскостей, скрещивающихся прямых; формулировки признаков и свойств параллельных прямых и плоскостей; простейшие приемы изображения фигур в стереометрии и приемы чтения их свойств по чертежу.	определения параллельных прямых и плоскостей, скрещивающихся прямых; формулировки признаков параллельности; свойства параллельных плоскостей, построение плоскости, параллельной данной; свойства параллельной проекции и приемы изображения фигур в стереометрии; приемы: док-ва теорем; решения типовых задач и выполнения чертежа по условию задачи	структуру определений и теорем; различные идеи и методы доказательства (аксиоматический, дополнительных построений, метод «от противного»; приемы решения задач на доказательство и их переноса в нестандартные ситуации.
2.	Понимание	Ученик
	Готовность к преобразованию изученного из одной формы в другую, к его интерпретации	узнает параллельные прямые и плоскости на чертеже, в окружающей обстановке; правильно воспроизводит термины, краткую запись задач и чертеж, цели и частные приемы решения учебных заданий; приводит примеры параллельных прямых и плоскостей на предметах окружающего мира	интерпретирует свойства параллельных прямых и плоскостей на чертежах, моделях, использует таблицы, схемы; приводит контрпримеры к понятиям, различает определения, признаки и свойства параллельных и скрещивающихся прямых и плоскостей; выделяет ситуации применимости приемов решения типовых задач.	преобразует словесный и геометрический материал, связанный с параллельностью прямых и плоскостей, в символический, и обратно; выводит следствия из определений, доказывает эквивалентность определений; выделяет идеи и методы доказательства; находит новые приемы решения задач на доказательство.
3.	Умения и навыки	Ученик
	Выполнение дейст-вий, составляющих прием учебной деятельности, под активным контро-лем внимания или автоматизировано	решает простейшие задачи на доказательство параллельности прямых и плоскостей, на вычисление по данным алгоритмам или с помощью извне; изображает фигуры; записывает и оформляет решение задач на доказательство.	решает типовые задачи на доказательство параллельности прямых и плоскостей и вычисление, используя все необходимые приемы их решения;	решает типовые и прикладные задачи на доказательство в нестандартных ситуациях, самостоятельно выбирает и использует методы доказательства.

4. Выберите ответ из числа предложенных, укажите в ответе соответствующую букву.

– Прямые с и d принадлежат плоскости β. Могут ли прямые с и d быть параллельными?

– Прямые а и в параллельны. Прямая с пересекает прямую а, но не пересекает в. Как расположены прямые с и в?

а) параллельны; б) пересекаются; в) скрещиваются.

– Прямая а пересекает плоскость α. Может ли в плоскости α лежать прямая, параллельная а?

5. Ответьте на вопросы и сделайте соответствующие пояснения (рисунки):

– Сколько случаев взаимного расположения прямой и плоскости в пространстве?

– Сколько можно провести через данную точку прямых, параллельных данной плоскости?

– Сколько можно провести через данную точку плоскостей, параллельных данной прямой?

6. Известно, что прямая параллельна плоскости.

а) Параллельна ли она любой прямой в этой плоскости? Ответ поясните.

б) Может ли данная прямая пересечь хотя бы одну из прямых этой плоскости? Ответ обоснуйте.

в) Какие могут быть случаи расположения данной прямой с другими прямыми этой плоскости?

7. Как могут быть расположены прямая а и плоскость α, если данная прямая и некоторая прямая, лежащая в плоскости α, скрещиваются? Сделайте рисунок и поясните ответ соответствующими записями.

– Если прямая а параллельна плоскости α и прямая b параллельна прямой а, то прямая b параллельна плоскости α. (Рассуждайте методом от противного). Сделайте рисунок.

– Если прямые а и b параллельны плоскости α, то и прямая b параллельна прямой а. (Ответ обоснуйте, приведите контрпример и сделайте соответствующие пояснения и рисунок).

Математические задачи для классов различного профиля и их решение

Замечание 1. Примеры математических задач для классов различного профиля приведены при выполнении общего задания 2.

Замечание 2. Примеры решения задач приведены при выполнении общего задания 3.

Методика обучения решению тригонометрических уравнений

Методика обучения решению тригонометрических уравнений включает следующие ключевые вопросы:

1) изучение решения тригонометрических уравнений:

б) уравнений, которые после введения новой переменной приводятся к квадратным;

в) однородных тригонометрических уравнений (1-го и 2-го порядков);

г) уравнений, для решения которых надо разложить на множители левую часть, приравняв затем каждый множитель к нулю.

2) подбор учебных задач, на формирование умений приводить тригонометрические уравнения к простейшему виду, к одинаков углам, к одинаковым функциям, к однородным уравнениям.

3) анализ, вывод и обобщение общего приема решения тригонометрических уравнений.

Примеры учебных задач, на усвоение общего приема решения

1. Приведите примеры тригонометрических уравнений.

2. Придумайте тригонометрические уравнения, функции в которых имеют одинаковые углы.

3. Из предложенных уравнений выберите те, в которых тригонометрические функции имеют одинаковые углы:

а) sin²2x + cosx + c = 0; б) sin²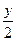+ cosy + b = 0; в) sin² α + cos α + c = 5.

4. Приведите тригонометрические функции, входящие в уравнения, к одинаковым углам: а) 3cos2x + sin²x + 5 sinx cosx = 0; б) 3 + sin 2x = 4sin²x; в) 2 + cos²x = cos .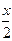

5. Сделайте замену в данных тригонометрических уравнениях:

Общий прием решения тригонометрических уравнений можно представить в виде блок-схемы.

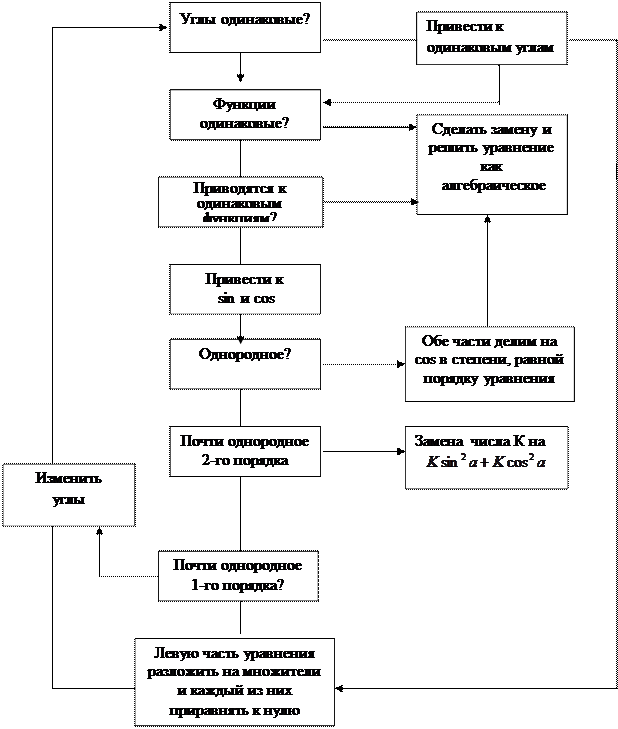Блок-схема решения тригонометрических уравнений

6. Из предложенных уравнений выберите однородное:

7. Придумайте тригонометрические уравнения, которые были бы однородными.

8. Из предложенных уравнений выберите почти однородные тригонометрические уравнения:

а) 3cosx + 2 sinx = 5; б) cos²x + 2 cosx sinx = 1; в) 3sin²x – 5 sinx cosx = – 2 cos²x.

9. Разложите левую часть тригонометрического уравнения на множители:

а) 2sin 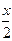cos 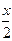– 2cos² 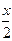; б) cos 3x – 1 = cos 2x; в) sin 3x cos 3x = sin 5x.

Учебные задачи, направленные на достижение развивающих целей

по теме «Многогранники» (выполнила Т. Злыгостева 53 м.)