II уровень. Тема: Применение производной в физике и технике (10 класс, 2 часа)

Практическая работа

Тема: Применение производной в физике и технике (10 класс, 2 часа)

Цели урока:

1. Определить физический смысл производной, рассмотреть использование механического истолкования производной при решении задач, связанных с ним, расширить знания учащихся и ввести понятия производной второго порядка, используя ее физический смысл.

2. Развивать логическое мышление при установлении связи физических величин с понятием производной, развивать монологическую речь в ходе объяснений, обоснований выполняемых действий, развивать навыки самостоятельной работы.

3. Воспитывать интерес к изучаемому материалу.

Оборудование: таблицы по определению производной, раскладные карточки по правилам дифференцирования, перфокарты, карточки для осуществления обратной связи.

К данному уроку учащиеся готовят ответы на вопросы, используя предложенную литературу:

1. О происхождении терминов «производная» и «предел» и их обозначения.

2. Физический смысл производной.

3. Применение производной в физике.

4. Применение производной в технике.

Кроме того, они должны подобрать задачи, в которых выясняется физический смысл производной.

Девиз урока: «Добывай знания сам!»

Ход урока

Учитель: Изучение материала по теме урока имеет принципиально важное значение, так как здесь показывается приложение производной к решению различных физических задач, т. е. возможности применения элементов дифференциального исчисления в описании и изучении процессов и явлений реального мира. Дифференциальные исчисления связаны с понятием производной.

Вопрос: Что называется производной?

Сообщение учащегося: 1) о происхождении терминов и обозначений производной и предела; 2) из истории дифференциального исчисления.

Учитель: Часто можно слышать, что математики и физики – это лирики. Софья Ковалевская говорила: «Математик должен быть поэтом в душе».

Приведу слова из учительского фольклора (с использованием таблицы «Алгоритм нахождения производной»).

В данной функции от х, нареченной игреком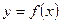

Вы фиксируете х, отмечая индексом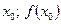

Придаете вы ему тотчас приращение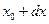

Тем у функции самой вызвав изменение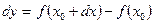

Приращений тех теперь взявши отношение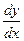

Пробуждаете к нулю dх стремление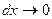

Предел такого отношения вычисляется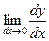

Он производною в науке называется у^| =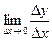

Одно из применений производной основывается на её геометрическом смысле.

Вопрос: В чем суть геометрического смысла производной?

Проблемная задача: Две материальные точки движутся прямолинейно по законам:

S₁ (t) = 2.5 t² – 6 t+1; S₂ (t) = 0.5 t² + 2 t – 3; В какой момент времени скорости их равны, т. е. V₁ (t₀) = V₂ (t₀), t₀ =?

Учитель: Рассмотрим физический смысл производной. Учащиеся, которые готовили этот вопрос, будут «защищать диссертацию».

(Остальные дите делают записи в тетрадях и уточняют непонятные моменты).

Сообщение учащегося: о применении производной в физике и технике.

Класс решает предложенную проблемную задачу.

Закрепление и проверка уровня усвоения

Вопросы: В чем заключается физический смысл первой производной?

В чем заключается физический смысл второй производной?

Учащимся предлагается заполнить таблицу:

Таблица 26

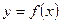
	Геометрический смысл	Физический смысл

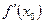
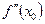
Задача 1. Точка движется прямолинейно по закону S(t) = 2 t³ – 3 t. Вычислите скорость движения точки: а) в момент времени t; б) в момент t₀ = 2с.

Задача 2. Найдите скорость и ускорение для точки, движущейся по закону

S(t) = t³ + 2 t + 3: а) в момент времени t; б) в момент t₀ = 3 с.

Самостоятельная работа

Учащиеся выполняют задания устно и на вопрос учителя поднимают карточку с правильным ответом.

Вариант № 1.

1. В чем сущность физического смысла у ^/?

А) Скорость Б) Ускорение В) Угловой коэффициент Г) Время

2. Точка движется по закону S(t) =2 t³ +3t. Чему равна скорость в момент t₀ = 1 с?

А) 15 Б) 12 В) 9 Г) 3

3. Зависимость пути S от времени движения выражается формулой S = 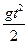. Чему равно ускорение?

А) 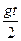Б) 2gt В) gt Г) g

4. Точка движется прямолинейно по закону S(t) = t³/3 – 2 t²+3 t+1. В какие моменты времени её скорость будет равна нулю?

А) 1 и 3 Б) 1 и 4 В) 2 Г) 2 и 0

5. Скорость тела, движущегося прямолинейно, определяется по формуле

V(t) = 5 t³ + t². Чему равно ускорение тела в момент времени t₀ = 1с?

А) 17 Б) 32 В) 30 Г) 16.

Ответы, которые должны показать ребята:

Вариант 1

А

В

Г

А

А

Итог урока. При подведении итогов урока учитель еще раз подчеркивает суть геометрического и физического смысла первой и второй производной, связь математики и физики.

Задание 12

Обобщение и систематизация темы

«Объемы и площади многогранников и тел вращения»

(фрагмент урока, 11 класс)

Дата добавления: 2014-12-27