Вопросы к экзамену. 1) Геометрические фигуры: определения, свойства

Вопросы к зачету

1) Геометрические фигуры: определения, свойства. Методика изучения геометрических фигур и их свойств на примере темы «Четырехугольники».

2) Задачи на построение. Методика изучения геометрических построений в пропедевтическом и систематическом курсе геометрии основной школы.

3) Геометрические величины. Решение геометрических задач на вычисление, метод площадей. Методики изучения площадей фигур в курсе математики основной школы.

4) Геометрические преобразования: движение, подобие. Методика изучения геометрических преобразований в пропедевтическом и систематическом курсе геометрии.

5) Векторы в школьном курсе геометрии. Решение задач векторным методом. Методика изучения темы «Векторы на плоскости» в курсе планиметрии.

6) Декартовы координаты на плоскости. Решение задач методом координат. Методика изучения координат в курсе математики основной школы.

III. Экзамен проводится в 8 семестре и включает вопросы специальной методики обучения геометрии и алгебре в основной школе, а также отдельные вопросы по общей методике: методика изучения понятий, теорем, методика обучения решению задач, методы обучения.

Теоретическая часть

1. Общедидактические методы обучения математике (рассказ, беседа, самостоятельная работа, эвристический метод и др.).

2. Методы психологии в обучении математике (анализ, синтез, сравнение, обобщение, абстрагирование, классификация, систематизация).

3. Понятие педагогической технологии. Основные параметры технологии обучения. Технологии обучения математике.

4. Методы логики в обучении математике (индукция, дедукция, аналогия).

5. Методы математики в обучении математике (аксиоматический метод, метод математического моделирования, обучение через задачи).

6. Математические понятия и методика их изучения в школьном курсе математики.

7. Математические предложения и доказательства; методика их изучения в школьном курсе.

8. Задачи в обучении математике. Задачи как средство обучения и как цель обучения.

9. Числа и вычисления в школьном курсе математики и методика их изучения.

10. Математические выражения и тождественные преобразования выражений; методика их изучения в школьном курсе математики.

11. Уравнения и неравенства в школьном курсе математики; методика их изучения.

12. Понятие функции; функции в школьном курсе математики; методика их изучения.

13. Логические основы школьного курса геометрии и методика их изучения в средней школе.

14. Геометрические фигуры и их свойства и методика их изучения.

15. Геометрические построения на плоскости и методика их изучения.

16. Геометрические величины в школьном курсе геометрии; методика их изучения.

17. Геометрические преобразования в школьном курсе геометрии, понятие равенства и подобия фигур; методика их изучения.

18. Координаты и метод координат в школьном курсе математики и методика изучения.

19. Векторы в школьном курсе геометрии и методика их изучения.

Практическая часть

Решить математическую задачу. Сформулировать общий прием решения и частные приемы. Составить несколько учебных заданий на формирование умений решать задачи такого типа.

1. Найти наименьшее натуральное решение неравенства: .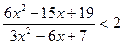

2. Решить двумя способами задачу:

3. В фермерском хозяйстве под зерновыми культурами занято 52,5 кв. км. Рожь занимает 2/5, а пшеница 1/3 всех посевов, остальную часть занимает ячмень. Сколько гектаров занимает ячмень?

4. Докажите, что биссектрисы внешнего угла при вершине равнобедренного треугольника параллельны основанию.

5. Докажите векторным методом, что диагонали ромба перпендикулярны.

6. Постройте график функции и укажите интервалы знакопостоянства и монотонности функции у=2х²-4х+3.

7. Высоты треугольника АВС, проведенные из вершин А и С, пересекаются в точке М. Найдите угол АМС, если ÐА = 70°, ÐС = 80°.

8. Постройте треугольник по стороне и проведенным к ней медиане и высоте.

9. При симметрии относительно некоторой прямой точка Х переходит в точку Х¢. Постройте точку, в которую при этой симметрии переходит точка Y.

10. Даны точки А (-1;-1) и С (-4;3). Составьте уравнение окружности с центром в точке С, проходящей через точку А.

Ответы на вопросы нужно строить по плану, включающий в себя план лекций и выполнения заданий к семинарам.

Ответы на теоретические вопросы билета нужно строить по плану, включающий в себя план лекций и выполнения заданий к семинарам.

Примерный план ответа на экзамене

1. Характеристика математического содержания материала данной содержательно-методической линии. Для конкретной темы – указать ее принадлежность к той или иной линии.

2. Место данной линии (темы) в программе, цели ее изучения.

3. Основные типы математических и учебных задач, требования к математической подготовке учащихся. Решение математической задачи с выполненным методическим заданием.

4. Основные положения методики изучения данной темы, методической линии в основной школе (преобладающие методы обучения, характерные методические приемы организации учебной деятельности учащихся, методические схемы).

5. Примеры (фрагменты уроков), иллюстрирующие п.п. 2–4.

Критерии оценки ответа на экзамене

Студент получает оценку «удовлетворительно», если он при ответе полностью раскрыл любые три пункта плана (или дал краткие ответы на все пункты плана).

Студент получает оценку «хорошо», если он при ответе полностью раскрыл любые четыре пункта плана (обязательным является выполнение п. 5).

Студент получает оценку «отлично», если при ответе он полностью раскрыл все пункты плана.

РАЗДЕЛ IV

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ

Дата добавления: 2014-12-27