Задачи аппроксимации и интерполяции

Аппроксимация, интерполяция функций

Способы оценки погрешности

Источники погрешности

В теоретических исследованиях выделяют следующие источники погрешности:

- погрешность исходных данных;

- погрешность математической модели, связанную с тем, что не рассматриваются факторы и явления, мало влияющие на исследуемые процессы;

- погрешность метода, связанную с тем, что идеальные математические объекты и операции могут заменяться их приближенными аналогами (производная - на отношение разностей, интеграл - на конечную сумму и т.п.);

- погрешность округления, связанную с количеством удерживаемых значащих цифр в расчетах, которая при машинном счете зависит от типа используемых переменных.

Считается рациональным, если каждый из этапов преобразования данных несущественно увеличивает погрешность. Поэтому погрешность каждого из перечисленных типов должна быть меньше погрешности предыдущего типа.

После получения результатов расчетов следует сравнить их погрешность с допустимой погрешностью, которая обычно диктуется конкретными условиями. Если погрешность велика (больше допустимой), то нужно найти главный источник погрешности и, устранив его, повторить исследование.

При оформлении результатов расчетов числовые данные следует записывать с количеством значащих цифр, соответствующим точности исходных данных.

Различают априорную и апостериорную оценки погрешности.

Априорная оценка погрешности - та, которая может быть получена до решения задачи. Она позволяет сначала определить, при каких параметрах математической модели может быть получена удовлетворительная точность и только после этого провести решение поставленной задачи. Такая последовательность действий является наиболее рациональной. Однако на практике получить априорную оценку погрешности удается нечасто.

Апостериорная оценка погрешности - та, которая получается после (в результате) решения задачи. Для этого, как правило, необходимо получить несколько решений задачи с различными параметрами математической модели. Такой подход более трудоемок, но обычно он бывает единственно возможным.

Часто функции либо имеют очень громоздкое аналитическое выражение, либо заданы таблично. В этом случае имеет смысл на некотором интервале заменить заданную функцию y(x) приближенным аналитическим, легко вычисляемым выражением j(х).

Постановка задачиаппроксимации: задана функция 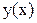. Требуется найти в аналитическом виде функцию 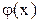, которая на некотором интервале 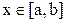приближенно равна исходной:

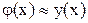. (2.1)

Функция 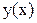называется аппроксимируемой, функция 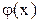- аппроксимирующей функцией или - коротко - аппроксимацией. Интервал - интервал аппроксимации.

Общая методика аппроксимации:

1) сначала подбирают такой вид аппроксимирующей функции 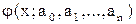, чтобы ее поведение на интервале аппроксимации качественно соответствовало поведению функции ;

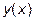2) затем определяют числовые значения свободных параметров 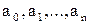таким образом, чтобы обеспечить приближенное равенство

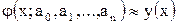
(2.2)

на интервале аппроксимации.

Интерполяцией (лагранжевой) называется такая аппроксимация, при которой равенство (2.1) или (2.2) понимается как совпадение функции 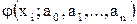с таблично заданной функцией 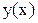в (n+1)-й точке:

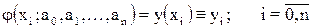. (2.3)

Точки х_i называются узлами интерполяции, а совокупность узлов - сеткой.

После решения системы (n+1)-го уравнения (3) относительно (n+1)-го параметра интерполяции 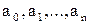интерполирующая функция 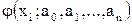полностью определена и, таким образом, задача интерполяции решена.

Интерполяция (аппроксимация) линейна, если свободные параметры 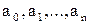присутствуют в функции в линейном виде:

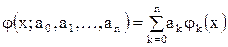. (2.4)

После подстановки (4) в (3) задача интерполяции сводится к решению системы линейных уравнений относительно искомых параметров а_к:

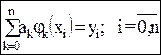(2.5)

Для существования и единственности решения задачи линейной интерполяции (решения системы (5)) необходимо и достаточно, чтобы

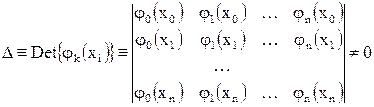(2.6)

Система функций 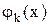, удовлетворяющая этому условию при любом расположении узлов, называется чебышевской.

Дата добавления: 2014-12-27