Интерполяционный многочлен Ньютона

Наиболее проста и универсальна интерполяция степенными функциями

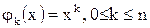. (2.7)

Можно показать, что условие (6) при этом всегда выполняется и, таким образом, степенной интерполяционный многочлен

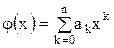(2.8)

всегда существует и единствен. Ньютону удалось построить такой многочлен, не прибегая к решению системы уравнений вида (5).

Разделенные разности функции :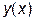

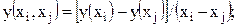(1-я)

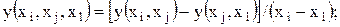(2-я) (2.9)

...

Свойство разделенных разностей: порядок следования аргументов в них не играет роли.

Пусть - многочлен степени n. Тогда первая разделенная разность для него

- (2.10)

- многочлен степени n-1. Вторая разделенная разность

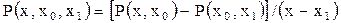(2.11)

- многочлен степени n-2. Наконец, n-я разделенная разность

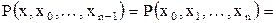
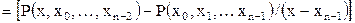(2.12)

- многочлен нулевой степени, константа. Решая равенство (10) относительно Р(х) и исключая из равенств (10) - (12) все разделенные разности, содержащие переменную х, получаем формулу

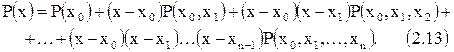Тт.к. по условию интерполяции

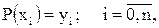(2.14)

то получаем интерполяционнуюформулу Ньютона

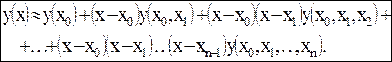(2.15)

Этот многочлен можно представить согласно схеме Горнера (ф-ла Ньютона - Грегори)

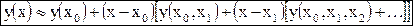(2.16)

Дата добавления: 2014-12-27