Определение погрешности

Погрешность

Динамика и прочность

Методическое пособие

ЗАДАЧ МЕХАНИКИ

Численные методы

для студентов специальности

Часть 1

Приближенные вычисления функций,

производных, интегралов

Системы линейных алгебраических уравнений

Проблема собственных значений

Нелинейные уравнения и системы

В.А. Федоров

Кафедра динамики и прочности машин

Харьковский государственный политехнический университет

Физические величины почти всегда известны приближенно, с погрешностью, если только речь не идет о целочисленных величинах или физических эталонах.

Погрешность (ошибка) некоторой величины 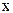- это разность между приближенным и точным значениями некоторой величины.

. (1.1)

Абсолютная погрешность величины 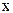- абсолютная величина погрешности: .

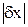Относительная погрешность величины 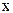- это отношение абсолютной погрешности к абсолютной величине приближенного значения:

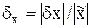(1.2)

В соответствии с определением (1.1) погрешность бывает известна точно только тогда, когда известно точное значение интересующей нас величины. В практических расчетах такая ситуация лишена смысла и поэтому обычно погрешность находят приближенно. Как правило, достаточно знать значение погрешности, округленное до первой значащей цифры. Более того, часто достаточно указать порядок величины абсолютной погрешности или оценку сверху и проводить исследования с ²запасом² точности.

Под понятием точность понимают количество верных значащих цифр в значении величины.

Приближенную величину 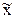можно рассматривать как переменную, принимающую значения в некоторой окрестности точки . Тогда, если задана некоторая функция 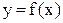, то оценить ее погрешность можно с помощью формулы для дифференциала:

. (1.3)

Аналогично для функции, зависящей от нескольких переменных 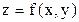, погрешность имеет вид

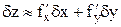. (1.4)

Дата добавления: 2014-12-27