Поперечное обтекание эллипсоида вращения

Поперечное обтекание эллипсоида вращения (рис.10), в отличие от продольного обтекания, не является осесимметричным, при этом картина течения в плоскостях, проходящих через некоторую ось, не одинакова. В случае поперечного обтекания эллипсоида вращения, функции тока не существует. Уравнение Лапласа в криволинейных координатах будет иметь вид

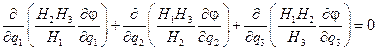
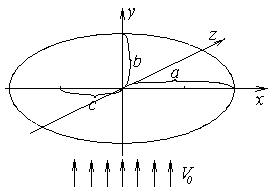
Рис. 10

Сохраняя ту же эллиптическую систему координат (l,m,e), что и при рассмотрении продольного обтекания эллипсоида вращения (см. пп. 1.1, 1.6), и учитывая выражения для коэффициентов Ламе

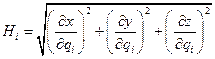, i=1,2,3,

запишем уравнение Лапласа в следующей форме

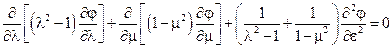
Будем искать потенциал течения как решение этого уравнения в виде произведения двух функций 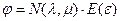; тогда, разделяя переменные, получим систему уравнений

,

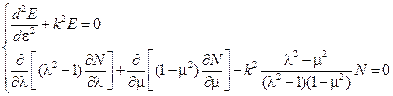где k – произвольное целое положительное число.

Первое уравнение имеет решение 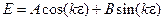, второе, если положить N=L(l)M(m) и разделить переменные, может быть приведено к системе уравнений

,

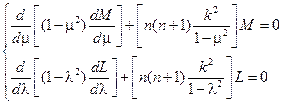имеющей в качестве частных решений присоединенные функции Лежандра

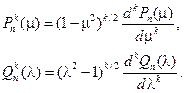
Комбинируя эти функции так, чтобы выражение потенциала скоростей возмущенного движения было ограниченным при l®¥ (в соответствии с условием (1.1.5)), получим общее выражение для потенциала скоростей

,

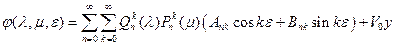где последнее слагаемое представляет собой потенциал набегающего потока, направленного вдоль оси y.

Довольствуясь решением, содержащим только cose, получим, что в выведенной формуле следующие коэффициенты примут значения

, , ,

,

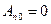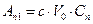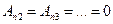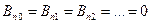и представив y как функцию l, m и e

,

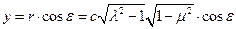получим выражение для потенциала поперечного обтекания тела вращения произвольной формы

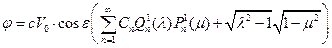. (1.7.1)

Для определения постоянных C_n необходимо составить граничное условие на поверхности обтекаемого тела. В случае пространственного движения тела функция тока отсутствует и необходимо непосредственно вычислять нормальную скорость 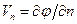и приравнивать ее нулю. Из этого получается следующее граничное условие

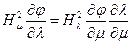, (1.7.2)

в котором l является заданной функцией от m согласно уравнению контура тела.

В случае эллипсоида вращения, обводы которого задаются условием

,

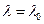граничное условие можно выполнить, положив в (1.7.1) коэффициенты C_n =0 при n >1, тогда m не будет входить в граничное условие. В этом случае уравнение (1.7.2) после определенных преобразований примет вид

,

откуда, подставив выражения для Q₁(l) (1.6.10), можно получить значение оставшегося коэффициента C₁

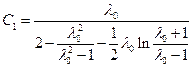. (1.7.3)

Потенциал скоростей поперечного обтекания эллипсоида вращения с учетом (1.7.3) принимает окончательный вид

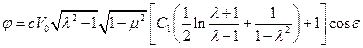(1.7.4)

Скорости определяются из потенциала по следующим формулам

, ,

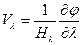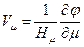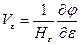
и в безразмерном виде представляются

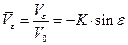, , (1.7.5)

, (1.7.6)

где 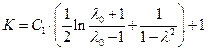. (1.7.7)

Порядок выполнения работы

Расчет начинается с определения обводов эллипсоида вращения (на плоскости 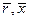- эллипса). Для этого нужно задать 10-15 точек 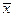, 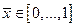. Интервал выбирается равным 0.1, в области оконечности эллипсоида (при 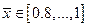) интервал желательно уменьшить до 0,05-0,025, и рассчитать значения 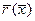для четверти эллипса с помощью уравнения

,

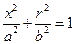из которого, с учетом вида безразмерных координат

, , ,

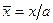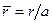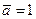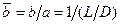
можно выразить :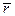

.

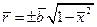Затем необходимо выбрать поперечные сечения эллипсоида (если они не заданы), в которых будет производиться расчет поперечного обтекания. Обычно выбирают 3 - 4 сечения на половине эллипсоида: , , .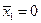

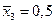
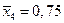Поперечное сечение эллипсоида вращения имеет форму круга. Нужно вычислить радиус каждого из этих сечений 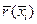и рассчитать для различных углов e значения безразмерных координат 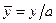и :

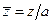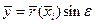, , i=1,2,3,4.

Угол e задается для четверти круга 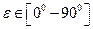с интервалом 10⁰-15⁰.

Затем необходимо рассчитать распределение значения проекций безразмерных скоросте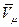й и 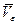по поверхности сечения эллипсоида, а затем и полной безразмерной скорости 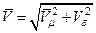, для этого в (1.7.3) и (1.7.6) необходимо учесть то, что 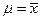, 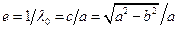. После этого можно рассчитать распределение коэффициента давления 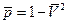по сечению.

В результате расчетов по заданному удлинению L/D должны быть получены следующие таблицы:

1) для обводов меридионального сечения эллипсоида

№
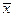
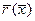
	0,0
….	…
	1,0

по этой таблице должно быть построено меридиональное сечение эллипсоида с обозначением расположения поперечных сечений.

2) для каждого поперечного сечения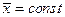

№	e, ^0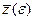
…
…

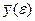
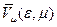
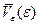
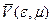
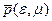
по этим таблицам должны быть построены графики для различных поперечных сечений эллипсоида, на которых в одном масштабе отложены зависимост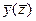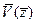и, , , и 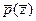. Принцип построения одного из таких графиков приведен на рис.11.

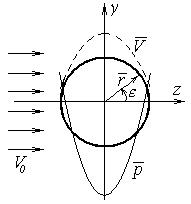
Рис. 11

Дата добавления: 2014-12-27