Продольное обтекание эллипсоида вращения

Рассмотрим продольное обтекание эллипсоида вращения (рис.9). Для решения задачи воспользуемся методом интегрирования уравнения Лапласа с помощью криволинейных координат. Удачный выбор криволинейных координат при решении уравнения Лапласа 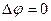позволяет наиболее просто удовлетворить граничным условиям, а также дает возможность разделить переменные в получающихся из уравнения Лапласа дифференциальных уравнениях.

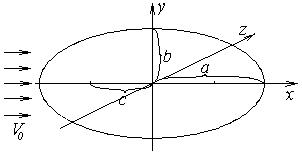
Рис. 9

Уравнение Лапласа в криволинейных координатах в случае осесимметричного обтекания (в плоскости меридионального сечения) имеет вид

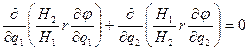(1.6.1)

где H_i (i=1,2) - коэффициенты Ламе:

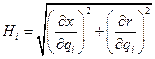. (1.6.2)

Для тел, близких к эллипсоидам без цилиндрической вставки, наиболее удобным оказалось использование эллиптических координат и 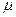. Описание этой системы координат приведено в п.1.1. (рис.4), связь эллиптических координат с цилиндрическими координатами x, r описывается формулами (1.1.6) и (1.1.7):

Если подставить уравнения (1.1.7) и (1.6.2) в уравнение Лапласа в криволинейных координатах (1.6.1), то можно получить следующий вид дифференциального уравнения Лапласа:

. (1.6.3)

Будем искать частное решение этого уравнения в виде произведения двух функций от переменных и 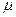в отдельности

, (1.6.4)

тогда в уравнении (1.6.3) переменные разделятся

.

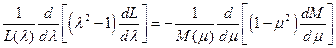В силу независимости и 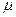следует, что каждая из частей записанного равенства должна быть постоянной. Полагая эту константу равной n(n+1), где n – целое положительное число, получим два уравнения Лежандра для L(l) и M(m):

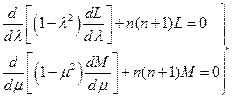. (1.6.5)

Этим уравнениям удовлетворяют полиномы Лежандра P_n(x)

, , ,

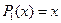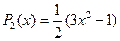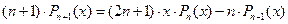для n³1;

и функции Лежандра второго рода Q_n(x):

, ,

,

для n³1.

Представим решение уравнения (1.6.3) как сумму потенциала j₀ набегающего потока со скоростью V₀

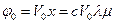(1.6.6)

и потенциала j^* вызванных скоростей, который выразим суммой частных решений в форме (1.6.4):

Остается неясным, как между этими функциями распределить аргументы (l и m). Этот вопрос можно решить, выполнив условие отсутствия вызванных скоростей на бесконечном удалении от тела (1.1.5). Потенциал вызванных скоростей течения (то есть обтекания за вычетом набегающего потока) при этом должен стремиться к нулю.

Необходимо учесть следующее: функция P_n(x), как полином n -й степени, обращается в бесконечность при x®¥, функция же Q_n(x) при этом стремится к нулю, но зато стремится к бесконечности при x=±1. В случае внешнего обтекания тела координата l=chx может достигать бесконечных значений, а координата m=cosh, ограничена.

Исходя из этого, для P_n выбираем аргументом m, а для Q_n - l. Соответственно, потенциал вызванных скоростей будет иметь вид

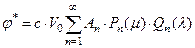, (1.6.7)

где A_n – постоянные коэффициенты, зависящие от формы поверхности тела.

Складывая потенциалы j₀ (1.6.6) и j^* (1.6.7), получим потенциал скоростей продольного обтекания тела вращения произвольной формы потоком со скоростью V₀:

. (1.6.8)

Для того, чтобы получить потенциал обтекания тела конкретной формы (в нашем случае – эллипсоида вращения), необходимо, чтобы j удовлетворял условию непротекания на поверхности тела.

Условие непротекания выполняется на любой линии тока, которую можно получить, приравняв функцию тока константе

,

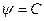для его выполнения на поверхности обтекаемого тела вращения следует принять С=0.

Уравнение нулевой линии тока для потенциала (1.6.8) имеет вид

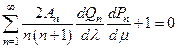. (1.6.9)

Для эллипсоида вращения, меридиональное сечение которого имеет уравнение

,

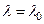в выражении (1.6.9) не должна присутствовать переменная m, следовательно, все P_n(m) кроме P₀(m) =1, должны отсутствовать. Это возможно, только если все коэффициенты A_n при n >1 будут равны нулю. Тогда (1.6.9) примет вид

при ,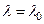

где 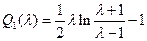. (1.6.10)

Отсюда можно найти A₁:

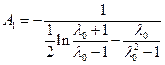. (1.6.11)

Подставляя значение А₁ и вид функций Q₁(l) и P₁(m) в выражение для потенциала, а также вводя эксцентриситет эллипса , где a - большая полуось эллипса, получаем окончательное выражение для потенциала продольного обтекания эллипсоида вращения

(1.6.12)

Проекции скорости на оси эллиптических координат будут иметь вид

,

.

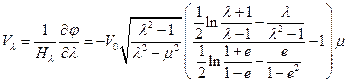Если в этих формулах положить 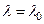, то мы получим выражения для скоростей на поверхности эллипсоида вращения. Нетрудно убедиться, что в этом случае , так как выполняется условие непротекания. Касательная к обводу эллипсоида составляющая скорости , равная полной скорости на поверхности эллипсоида, в безразмерном виде определяется зависимостью

. (1.6.13)

Порядок выполнения работы

Расчет начинается с определения обводов эллипсоида вращения (на плоскости 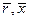- эллипса). Для этого нужно задать 10-15 точек 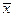, 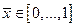. Интервал выбирается равным 0.1, в области оконечности эллипсоида (при 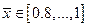) интервал желательно уменьшить до 0,05-0,025, и рассчитать значения 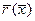для четверти эллипса с помощью уравнения

,

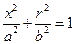из которого, с учетом вида безразмерных координат

, , ,

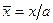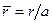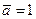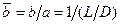
можно выразить :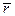

.

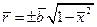Затем необходимо рассчитать распределение значения проекций безразмерной скорости по поверхности эллипса, для этого в (1.6.13) необходимо учесть то, что 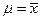, , а затем и коэффициента давления .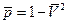

В результате расчетов по заданному удлинению L/D должна быть получена таблица для следующих величин

№
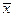
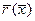
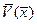
	0,0
….	…
	1,0

По этой таблице должен быть построен график, на котором в одном масштабе отложены зависимост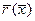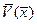и , , при .

Дата добавления: 2014-12-27