Обтекание кругового цилиндра

Поперечное обтекание бесконечного кругового цилиндра поступательным потоком является плоскопараллельным течением, которое можно свести к рассмотрению обтекания круга в плоскости xy.

Расчет обтекания цилиндра выполняется методом сложения простейших потенциальных потоков – поступательного потока вдоль оси x (1.1.8) и плоского диполя в начале координат (1.1.12).

Потенциал суммарного потока имеет вид

,

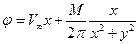но его удобнее записать в полярной системе координат rf

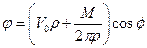. (1.2.1)

Функцию тока этого течения также можно получить сложением функций тока составляющих (1.1.9) и (1.1.13).

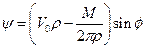. (1.2.2)

Приравнивая функцию тока нулю, можно получить уравнение нулевой линии тока

.

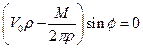У этого уравнения два решения, первое

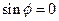
дает прямую линию, совпадающую с осью x, второе

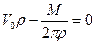(1.2.3)

дает выражение для r

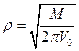. (1.2.4)

Так как момент диполя и V₀ – постоянные величины, то если обозначить

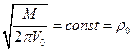, (1.2.5)

то из (1.2.3) получим уравнение окружности радиусом r₀ с центром в начале координат (рис.4).

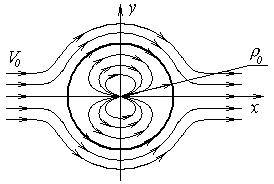
Рис. 4

Если заменить эту линию тока твердым телом, то на его поверхности будет выполняться условие непротекания

,

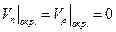так как нормаль к окружности - это ее радиус.

Таким образом, мы доказали, что потенциал (1.2.1) описывает обтекание кругового цилиндра потоком невязкой жидкости.

Выразим момент диполя через радиус цилиндра из (1.2.5):

,

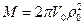тогда потенциал течения примет окончательный вид

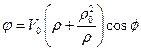. (1.2.6)

Из (37) можно получить выражения для скоростей V_r и Vf

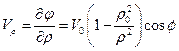, (1.2.7)

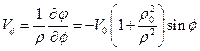, (1.2.8)

откуда видно, что при r=r₀, то есть на поверхности цилиндра,

, .

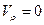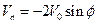Полная скорость на поверхности цилиндра

,

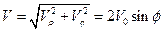при этом безразмерная скорость

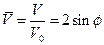, (1.2.9)

а значение коэффициент давления на цилиндре выражается формулой

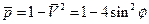. (1.2.10)

Порядок выполнения работы

По формулам (1.2.9) и (1.2.10) рассчитать значения 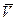и 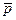на поверхности цилиндра (r=r₀).

Пользуясь формулами (1.2.7), (1.2.8) рассчитать 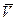и 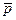на удалении от цилиндра (при r=1,5r₀, r=2r₀ или другом заданном расстоянии).

Расчеты проводить для четверти цилиндра (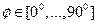 с интервалом 10⁰-15⁰).

В результате расчетов должна быть получена таблица следующего вида для каждого значения r:

№	(^0)
….	…	…
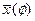
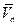
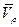
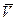
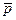
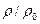
		0,0

По этим таблицам должны быть построены графики, на которых в одном масштабе отложены зависимост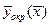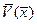и , , при 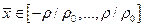, для каждого значения r.

Сравнить полученные графики и объяснить, чем вызвано различие в распределении скорости и давления на различных удалениях от поверхности цилиндра.

Дата добавления: 2014-12-27