Обтекание сферы

Обтекание сферы потоком невязкой жидкости со скоростью V₀ может быть получено наложением поступательного потока (1.1.8) на поток, генерируемый пространственным диполем (1.1.20).

Потенциал суммарного течения будет иметь вид

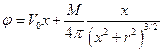, (1.7.1)

при этом потенциал обтекания диполя j можно представить в виде суммы потенциала набегающего потока и потенциала вызванных скоростей j_в:

. (1.7.2)

Функция тока суммарного течения также может быть получена путем сложения функций тока диполя и набегающего потока

. (1.7.3)

Момент диполя M пока остается неопределенной величиной. Найдем выражения для линий тока (точнее, это будут поверхности тока). Для этого приравняем функцию тока константе. Если эту константу взять равной нулю, то мы получим уравнение нулевой линии тока, которое будет иметь вид

(1.7.4)

Это уравнение имеет два корня: первый корень ­­r=0 соответствует оси x, второй корень

. (1.7.5)

Выражение (1.7.5) можно записать немного иначе, если перейти в сферическую систему координат. При этом 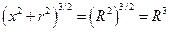, тогда второй корень уравнения (1.7.4) запишется в виде или . Так как подкоренное выражение является постоянной величиной, то если обозначить 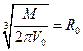, мы получим выражение для сферы радиусом R₀. Таким образом, нулевая поверхность тока состоит из оси x и поверхности сферы радиусом R₀.

Заменим часть поверхности тока, соответствующую сфере, твердой стенкой. В силу того, что на поверхности тока и на твердой стенке в невязкой жидкости выполняется одно и то же граничное условие непротекания, такая замена не повлияет на течение жидкости вне сферы, и мы получим обтекание невязкой жидкостью сферы радиусом R₀. При этом связь между радиусом сферы и моментом диполя M будет иметь вид

.

Подставляя эту зависимость в выражение для потенциала течения (1.7.1) и переходя к сферическим координатам, получим потенциал обтекания сферы заданного радиуса

. (1.7.6)

Из (1.7.6) можно получить проекции скоростей при обтекании сферы

, (1.7.7)

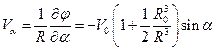. (1.7.8)

Подставляя в эти формулы R=R₀, получим скорости на поверхности сферы

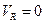, . (1.7.9)

Полная скорость на поверхности сферы

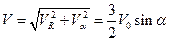, (1.7.10)

а коэффициент давления на сфере

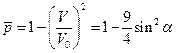. (1.7.11)

Порядок выполнения работы

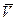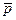По формулам (1.7.10) и (1.7.11) рассчитать значения и на поверхности сферы (R=R₀).

Пользуясь формулами (1.7.7), (1.7.8), (1.7.11) рассчитать 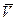и 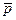на удалении от цилиндра (при R=1,5R₀, R=2R₀ или другом заданном расстоянии).

Расчеты проводить для четверти сферы ( с интервалом 10⁰-15⁰).

В результате расчетов должна быть получена таблица следующего вида для каждого значения R:

№	(^0)
….	…	…

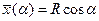
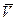
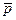
По этим таблицам должны быть построены графики, на которых в одном масштабе отложены зависимости 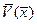, и обводы сферы для каждого значения R, где .

Сравнить полученные графики и объяснить, чем вызвано различие в распределении скорости и давления на различных удалениях от поверхности сферы.

Дата добавления: 2014-12-27