Основные теоретические сведения. Задачи гидромеханики напорных течений, у которых давление вдоль потока непостоянно, решают с помощью двух основных уравнений гидравлики – уравнения

Часть II

Гидравлика

Задачи гидромеханики напорных течений, у которых давление вдоль потока непостоянно, решают с помощью двух основных уравнений гидравлики – уравнения неразрывности и уравнения Бернулли для потока вязкой жидкости. Для потока несжимаемой жидкости они используются в следующем виде:

а) уравнение неразрывности для неразветвленного потока

; (2.1.1)

б) уравнение Бернулли для плавно изменяющегося установившегося потока несжимаемой вязкой жидкости

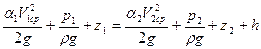. (2.1.2)

В выражениях (2.1.1), (2.1.2):

V_ср – средняя скорость в сечении,

,

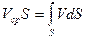S – площадь сечения потока;

Q – объемный расход;

a - коэффициент неравномерности кинетической энергии;

p – абсолютное давление;

z – высота над принятой горизонтальной плоскостью отсчета до точек, в которых давление равно p;

h – суммарные потери напора;

r - плотность движущейся жидкости.

Все слагаемые в уравнении (2.1.2) имеют размерность длины и поэтому называются высотами: 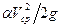- скоростная высота; ­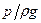 - ­приведенная высота давления; z – геометрическая высота.

Потери напора в трубопроводах подразделяют на два вида – потери напора на трение h_тр и местные потери напора h_м. Потери напора на трение происходят вдоль всего потока вязкой жидкости; местные потери локализуются на ограниченных по длине участках при изменении сечения потока, его направления, делении и слиянии, в арматуре и т. п.

Пренебрегая взаимным влиянием и используя принцип наложения, потери напора h представляют в виде суммы потерь на трение h_тр и местных потерь h_м.

Потери напора выражаются через безразмерные гидродинамические коэффициенты в долях от скоростного напора потока. Если он между входным и выходным сечениями элемента меняется, выбирают наиболее характерный и удобный, что должно быть оговорено.

Потеря напора на трение на участках равномерного течения вычисляется по формуле Дарси

, (2.1.3)

потеря напора в местных сопротивлениях – по формуле Вейсбаха

, (2.1.4)

где l - коэффициент потери напора на трение; l – длина участка трубопровода; d_г – гидравлический диаметр, для круглой трубы равный диаметру; z - коэффициент местной потери напора.

Коэффициенты l и z зависят от числа Рейнольдса, подсчитываемого по средней скорости и диаметру

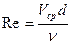. (2.1.5)

Коэффициент потерь на трение в общем случае зависит от числа Рейнольдса, отношения абсолютной эквивалентной шероховатости к диаметру k/d, т. е. относительной шероховатости e, и формы сечения канала.

Для круглых трубопроводов при ламинарном течении, когда Re <2300, справедлива формула Пуазейля

. (2.1.6)

Для турбулентного течения в гладких круглых трубопроводах используют различные полуэмпирические формулы, в том числе формулу Блазиуса (Re <10⁵)

. (2.1.7)

В области квадратичного сопротивления, то есть для сильно шероховатых труб при высоких числах Re, l=f(e). Для однородной зернистой шероховатости справедлива формула Никурадзе

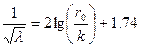, (2.1.8)

где r₀ – радиус трубы.

Для гидравлически гладких труб, области квадратичного сопротивления и переходной области при турбулентном течении может использоваться упрошенная универсальная формула А.Д.Альтшуля

, (2.1.9)

или ее степенная аппроксимация

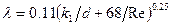. (2.1.10)

В формулах (2.1.9) и (2.1.10) k₁ – приведенная линейная характеристика шероховатости, приближенно равная 0.1 эквивалентной зернистой шероховатости k.

Коэффициенты местных потерь напора получают главным образом по результатам экспериментальных исследований. Необходимые для решения предлагаемых задач сведения приведены в разделе 2.3.

Дата добавления: 2014-12-27