Обтекание овоида

Основные формулы.

Используя метод наложения потоков, получим потенциал обтекания овоида – осесимметричного тела, образующегося при сложении пространственных источника и стока равной интенсивности с поступательным потоком, идущим в направлении источник-сток. Источник и сток расположим на оси x, на расстоянии a от начала координат, как показано на рис.4.

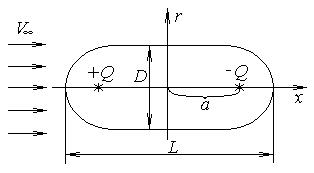
Рис. 8

Используя формулы (23)-(26), можно записать потенциал и функцию тока результирующего потока

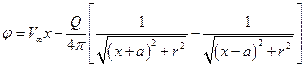; (33)

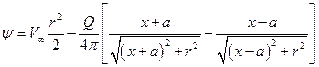. (34)

Проекции скорости имеют вид:

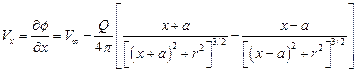(35)

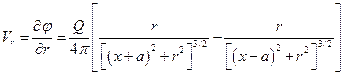(36)

Приравнивая функцию тока константе, можно получить семейство линий тока. Нулевая линия тока представляет собой овоид, уравнение поверхности которого определяется следующим уравнением:

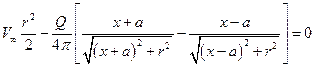. (37)

Для определения обводов овоида по формуле (37) нужно знать расстояние от начала координат до источника (стока) a и интенсивность источника (стока) Q.

Если задано удлинение овоида L/D, то задачу удобнее решать в безразмерном виде. Приняв в качестве характерной длины l половину длины овоида, в качестве характерной скорости 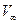скорость набегающего потока, введем следующие обозначения:

, ; , ;

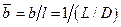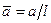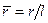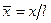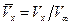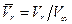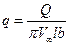, ; , (38)

где q – безразмерный коэффициент расхода.

Для точки тела с координатами x=0, 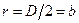, из уравнения (37) получим:

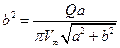или 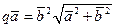. (39 а)

В критической точке (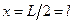, r=0) из (37) получим:

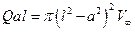или 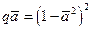. (39 б)

Если приравнять правые части (36а) и (36б), то можно получить уравнение для :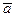

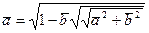. (40)

Коэффициент расхода определится по формуле

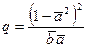. (41)

С учетом обозначений (38) перепишем уравнение обводов овоида (37) в безразмерном виде:

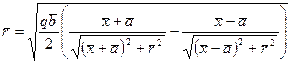. (42)

Скорости также можно записать в безразмерном виде

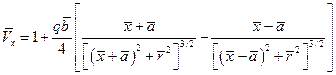, (43)

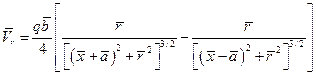. (44)

Порядок выполнения работы.

Расчет начинается с вычисления безразмерного расстояния от источника (стока) до начала координат 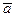по формуле (40):

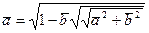
Неизвестная величина присутствует в обеих частях уравнения, которое решается методом итераций.

Для этого при заданном в правую часть уравнения (40) подставляется 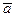, в первом приближении можно взять 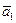= 0,8. Результат расчета 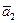, полученный в левой части уравнения сравнивается с 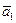. Если 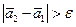, где e - погрешность расчета, то 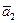подставляется в правую часть формулы и рассчитывается 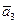. Значение 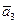также сравнивается с предыдущим значением (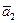). Расчет проводится до тех пор, пока разница между последующим и предыдущим расчетными значениями 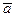не будет в пределах заданной погрешности e.

Затем рассчитывается q по формуле (41).

После этого необходимо получить обводы овоида. Для этого нужно задать 10-15 точек 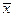, , 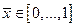в области цилиндрической вставки с интервалом 0,1, в области оконечности овоида с интервалом 0,05-0,025, и рассчитать значения функции 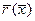для четверти овоида с помощью уравнения (42)

,

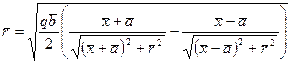которое также решается методом последовательных приближений для каждого значения .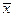

Имея значения 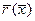, можно рассчитать распределение значения проекций безразмерной скорости по поверхности овоида (43), (44), а затем и распределение полной безразмерной скорости 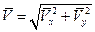и коэффициента давления .

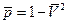В результате расчетов по заданному удлинению L/D должны быть получены величины (с указанием принятой величины погрешности e), и q, а также таблица значений следующих величин

№
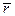
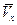
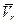
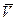
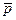
	0,0
….	…
	1,0

По этой таблице должен быть построен график, на котором в одном масштабе отложены зависимост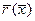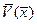и , , при .

Дата добавления: 2014-12-27