Финансовые ренты

Поток платежей, в котором все члены положительны, а временные интервалы между последовательными платежами одинаковы, называют финансовой рентой или аннуитетом.

Теория аннуитетов является важнейшей частью финансовой математики. Она применяется при рассмотрении вопросов доходности ценных бумаг, в инвестиционном анализе, страховании и т.д. Наиболее распространенные примеры аннуитета: регулярная выплата арендной платы, погашение долгосрочного кредита.

Основными параметрами финансовой ренты являются:

1 – член ренты R – величина каждого отдельного платежа;

2 – период ренты – временной интервал между двумя последовательными платежами;

3 – срок ренты – время от начала реализации ренты до поступления последнего платежа.

Дополнительными характеристиками являются:

- количество платежей в году;

- применяемая ставка процентов;

- частота начисления процентов;

- момент начисления процентов;

- момент выплаты члена ренты.

Ренты могут быть классифицированы по различным признакам:

· по количеству выплат члена ренты в течение года различают годовые и p-срочные (p раз в год):

· по частоте начисления процентов различают ренты с ежегодным начислением процентов, с начислением m раз в год, с непрерывным начислением. При этом момент начисления процентов может не совпадать с моментом выплат членов ренты;

· по величине членов ренты различают постоянные и переменные ренты;

· по надежности выплат ренты делятся на верные и условные;

· по количеству членов ренты различают ренты с конечным числом членов, ограниченные по срокам (срочные ренты) и с бесконечным числом членов (вечные ренты);

· по срокам начала действия ренты – немедленные и отложенные ренты;

· по срокам выплаты членов ренты (постнумерандо и пренумерандо).

Ренту, в которой платежи осуществляются в конце периода, называют аннуитетом постнумерандо. Ренту, в которой платежи осуществляются в начале периода, называют аннуитетом пренумерандо.

Если период ренты совпадает с периодом начисления процентов, то рента называется простой, в противном случае общей.

Аннуитеты различаются между собой следующими основными характеристиками:

- величиной каждого отдельного платежа;

- интервалом времени между двумя последовательными платежами (периодом аннуитета);

- сроком от начала аннуитета до конца его последнего периода (бывают и неограниченные по времени – вечные аннуитеты);

- процентной ставкой, применяемой при наращении или дисконтировании платежей.

Однако обобщающими параметрами любой ренты всегда являются наращенная стоимость и современная стоимость ренты. Несмотря на видовое различие, расчет наращенной или современной стоимости аннуитетов проводится по одним и тем же методикам, а именно:

Ø Наращенная стоимость аннуитета определяется как сумма наращенных стоимостей отдельных членов аннуитета;

Ø Современная стоимость аннуитета определяется как сумма дисконтированных стоимостей отдельных членов аннуитета.

В частности, задача вычисления современной стоимости простого постоянного срочного годового аннуитета постнумерандо может быть решена следующим образом:

Пусть в течение n лет в конце года вносится сумма в R руб. На взносы ежегодно начисляются сложные проценты по ставке i % годовых.

Графически данная задача может быть представлена следующим образом:

R

R

R

R

0 1год 2 год 3 год n-1 год n год

При заданной процентной ставке i современное значение каждого платежа на начало ренты будет определяться путем дисконтирования каждого члена ренты:

…

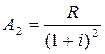
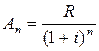
Как видим, приведенные стоимости платежей A₁, A₂, …, A_n представляют собой геометрическую прогрессию, в которой каждый член, начиная со второго, равен предыдущему, умноженному на одно и тоже число, равное 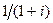. Это число называют знаменателем геометрической прогрессии и обозначают буквой q.

Сумма n первых членов геометрической прогрессии может быть вычислена по формуле:

.

Современная стоимость всего аннуитета как сумма членов геометрической прогрессии, составит:

(62)

где переменная n означает число периодов начисления, а i представляет собой ставку за период. В общем, период не обязательно должен быть равен одному году. Если в качестве периода выступает один квартал, то i является сложной ставкой за один квартал.

В формуле (62) множитель 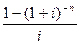называется коэффициентом дисконтирования ренты. Экономический смысл дисконтного множителя заключается в следующем: он показывает, чему равна сегодня стоимость аннуитета с постоянными денежными поступлениями в размере одной денежной единицы в течение n лет при заданной процентной ставке i. Этот множитель иногда называют фактором текущей стоимости обычного аннуитета или фактором Инвуда (английский экономист Уильям Инвуд). В финансовой практике для коэффициента приведения ренты используются следующие обозначения: FM4 (i, n) или a_n,i. Индекс n,i указывает на число периодов начисления и ставку за период. С учетом введенных обозначений формула (62) примет вид:

(63)

Для оценки будущей стоимости аннуитета постнумерандо необходимо найти наращенную на конец ренты стоимость каждого ее члена и сложить полученные величины. Проводя рассуждения, аналогичные вышеприведенным, получим следующее равенство:

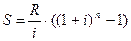(64)

В данной формуле множитель 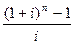называется коэффициентом наращения аннуитета. Экономический смысл этого множителя следующий: он показывает будущую суммарную стоимость аннуитета в одну денежную единицу к концу срока его действия. При этом предполагается, что за весь период аннуитета никаких изъятий не производится. Иногда множитель наращения аннуитета называют фактором будущей стоимости обычного аннуитета. В финансовой практике для коэффициента наращения ренты используются следующие обозначения: FM3 (i, n) или s_n,i. Индекс n,i указывает на число периодов начисления и ставку за период. С учетом введенных обозначений формула (64) примет вид:

(65)

Для оценки современной стоимости аннуитета пренумерандо используют формулу:

(66)

Наращенная сумма аннуитета пренумерандо может быть рассчитана следующим образом:

(67)

Заметим, что наращенная сумма аннуитета пренумерандо в 1+i раз больше аналогичной суммы ренты постнумерандо. Точно такая же зависимость наблюдается и между современными стоимостями рент постнумерандо и пренумерандо. Поэтому формулы (66)-(67) с учетом ранее введенных обозначений могут быть записаны в виде:

и (68)

Для оценки постоянного p-срочного аннуитета постнумерандо (p-число платежей в году, m-количество периодов начисления процентов в году) используются следующие формулы:

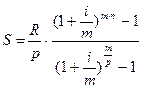(69)

(70)

В формулах (66)-(67) использованы следующие символические обозначения:

R – величина годового члена ренты;

p - число платежей в году;

m - количество периодов начисления процентов в году;

n – срок ренты в годах;

i – годовая ставка сложных процентов.

Если платежи в постоянном p-срочном аннуитете осуществляются в начале периода, то получаем ренту пренумерандо, будущая стоимость которой будет в больше стоимости, рассчитанной по формуле (69). Аналогичная зависимость существует и между современными стоимостями рассматриваемых аннуитетов. Т.о. для оценки постоянного p-срочного аннуитета пренумерандо получим следующие формулы:

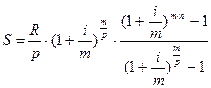(71)

(72)

Необходимо отметить, что формулы (62)-(72) позволяют оценить аннуитеты при декурсивном начислении процентов. При антисипативном начислении процентов по сложной учетной ставке d необходимо использовать другие формулы, вывод которых аналогичен выводу формулы (62).

В рассмотренных выше случаях аннуитетов платежи осуществлялись в течение определенного фиксированного времени. Однако на практике денежные поступления могут продолжаться достаточно длительное время. Такие аннуитеты называются бессрочными или вечными. К бессрочным аннуитетам относят аннуитеты, рассчитанные на 50 или более лет. В этом случае задача определения будущей стоимости аннуитета не имеет смысла. Однако текущая стоимость аннуитета может быть рассчитана по формуле:

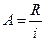(73)

В формуле (73) предполагается ежегодное начисление процентов и выплат членов ренты. Если же платежи осуществляются p раз в году, то текущая стоимость вечной ренты может быть рассчитана по формуле:

(74)

Безусловно, рассмотренные нами финансовые ренты не исчерпывают всего их видового многообразия. В частности, за пределами нашего пособия остались ренты с переменными членами, а также непрерывные ренты. Однако даже рассмотренные случаи позволяют решать достаточно широкий класс практических задач.

Пример 36 Вам предлагают сдать в аренду участок на три года, предлагая различные условия оплаты:

1. 10 тыс. руб. в конце каждого года;

2. 10 тыс. руб. в начале каждого года;

3. 2,5 тыс. руб. ежеквартально;

4. 35 тыс. руб. в конце трехлетнего периода.

Выберите из предлагаемых условий наиболее оптимальный вариант.

Дата добавления: 2014-12-27