Предел последовательности и его свойства

Число a называется пределом последовательности { а_n }, если для любого наперед заданного положительного числа e найдется такое натуральное число N, что для любого номера элемента n > N выполняется неравенство: | a_n – a | < e.

В этом случае пишут .

Другими словами, какую бы точность e мы не задали, начиная с некоторого номера n > N все члены последовательности будут отличаться от значения предела а на число, меньшее e, т.е. будут близки к числу а.

Геометрически определение предела последовательности можно представить следующим образом: при достаточно больших значениях п элементы последовательности практически не отличаются от числа а (рис. 8.4). Говорят, что такие элементы попадают в e- окрестность числа а.

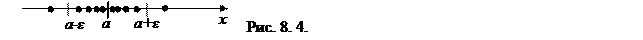
Так, в примере 8.1 с возрастанием номера п элементы последовательности 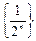все ближе и ближе приближаются к числу 0 (рис. 8.4). Покажем, что .

Выберем любую точность e >0(например, e= 0,001). Тогда найдется натуральное число N (в нашем случае N =9), такое что для всех n > N выполняется неравенство: < e (в нашем примере уже для п =10 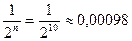будет меньше e= 0,001).

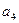
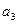
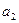
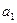
х

Рис. 8.4.

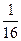
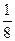
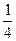
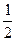0 1

В примере 8.3 с возрастанием номера п элементы последовательности { } приближаются к числу 0, и аналогично можно показать, что .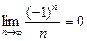

Последовательность, имеющая предел, называется сходящейся, а не имеющая предела – расходящейся.

Так, в примере 8.2 последовательность {3 п -2} не имеет предела, т.к. ее элементы неограниченно возрастают, следовательно, эта последовательность является расходящейся.

Последовательности, рассмотренные в примерах 8.1 и 8.3 являются сходящимися.

Еще до нашей эры философом Зеноном Эллийским (490-430 г.до н.э.) были рассмотрены задачи, содержащие в себе противоречия. Их так и называют – апории Зенона. Рассмотрим одну из таких задач, которая носит название дихотомия.

Пусть пешеходу нужно пройти из пункта А в пункт В. Для этого он должен сначала преодолеть половину пути, потом половину оставшегося расстояния, затем следующую половину и т.д.

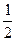
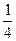
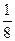
А 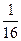В

Следовательно, пешеход пройдет сначала 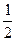пути, затем 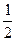+ 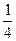пути, затем 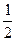+ + 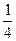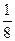пути и т.д. Какой бы маленький участок пути ни оставалось преодолеть пешеходу, очевидно, что у любого, даже самого маленького отрезка, всегда можно найти половину. И путнику вновь останется преодолеть половину этого маленького отрезка. И так до бесконечности! Парадоксально, но факт, пешеходу все время придется делить оставшийся отрезок пополам, и он никогда не придет в пункт В.

Если составить алгоритм решения задачи в контексте данной логической схемы, то ни один компьютер не справится с ней – «зависнет», он будет продолжать находить середину отрезка до прерывания программы.

Посмотрим на эту задачу с точки зрения теории пределов. Расстояние, которое должен преодолеть пешеход, можно представить как сумму первых п элементов последовательности 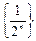: 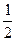+ + 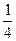+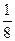…+ 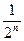=1- 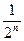. Найдем предел этой последовательности: . Значит, с возрастанием п длина отрезка, которую остается преодолеть пешеходу, становится ничтожно мала, и пешеход все-таки придет в пункт В!

Для практического нахождения пределов числовых последовательностей используют следующие свойства пределов:

Пусть { а_n } и { b_n } – сходящиеся последовательности, т.е. , 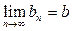. Тогда справедливы следующие утверждения:

1. Всякая сходящаяся последовательность имеет только один предел.

2. Для любого числа k последовательность { kа_n } также сходится, причем = .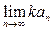

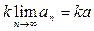3. Сумма (разность) а_n± b_n также сходится, причем

= .

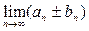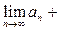
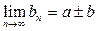4. Произведение а_n b_n также сходится, причем

= .

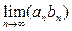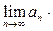
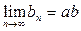5. При дополнительном условии b≠0 частное 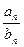также сходится, причем .

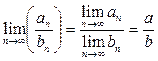Пример 8.4. Найдите предел .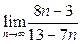

Решение. Числитель и знаменатель представляют собой расходящиеся последовательности (так как они не ограничены), поэтому непосредственно применять теорему о пределе частного нельзя. В этом случае поступим так: числитель и знаменатель разделим на п (от этого дробь не изменится), а затем применим доказательные теоремы о пределах последовательностей. Приведем подробную запись вычисления предела:

.

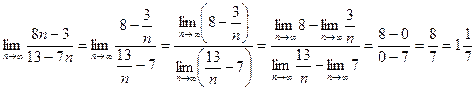Ответ: = .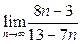

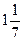Дата добавления: 2014-12-27