Признак сходимости монотонной последовательности. Число е

Не всякая последовательность имеет предел. Сформулируем признак существования предела последовательности.

Теорема Вейерштрасса. Всякая монотонная ограниченная последовательность имеет предел.

В качестве примера рассмотрим последовательность а_n= 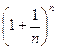. Выпишем элементы этой последовательности:

п =1, а₁= 2;

п =2, а₂= 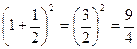= 2,25;

п =3, а₃= 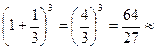2,37;

п =4, а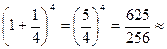₄= 2,44.

Видим, что каждый следующий элемент последовательности больше предыдущего. Данная последовательность является возрастающей.

Кроме того, данная последовательность ограничена, при этом для любого п 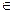N справедливо неравенство: 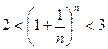. Следовательно, на основании теоремы Вейерштрасса последовательность а_n= 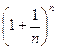имеет предел, равный е: 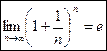. Существование этого предела впервые установил Д.Бернулли в 1728 году.

Число е – иррациональное число, его приближенное значение равно 2,72 (е = =2,718281828459045…). Число е называют неперовым числом, а обозначение е введено Эйлером в начале ХVIII века.

Отметим, что число е является основанием логарифма, получившего название натурального: lnx=log_ex. Натуральные логарифмы наиболее часто употребляются на практике.

Контрольные вопросы.

1. Что называют числовой последовательностью?

2. Какая числовая последовательность называется возрастающей? Убывающей? Приведите примеры возрастающих и убывающих числовых последовательностей.

3. Какая числовая последовательность называется ограниченной?

4. Дайте определение предела последовательности.

5. Какими свойствами обладает предел последовательности?

6. Какие последовательности называются бесконечно малыми? Бесконечно большими?

7. Как связаны бесконечно малые и бесконечно большие последовательности?

8. Сформулируйте признак сходимости монотонной последовательности.

Дата добавления: 2014-12-27