Лекция 10. Непрерывность функции

План:

1. Непрерывность функции в точке и на промежутке.

2. Основные теоремы о непрерывных функциях.

3. Свойства функций, непрерывных на отрезке.

4. Непрерывность элементарных и сложных функций.

5. Точки разрыва, их классификация.

1. Непрерывность функции в точке и на промежутке

Пусть функция у=f(x) определена в точке х_о и некоторой окрестности этой точки.

Функция у=f(x) называется непрерывной в точке х_о, если существует предел функции в этой точке и он равен значению функции в этой точке, т.е.

.

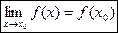Пример 10.1. На основании определения непрерывной функции выясните, являются ли функции у=f(x) и у=g(x) на рис. 10.1 и 10.2 непрерывными в точке х =1.

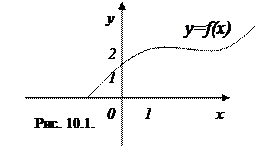
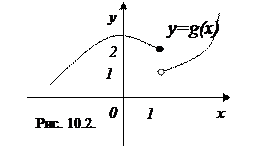
Решение: Функции у=f(x) и у=g(x) определены в точке х =1 и некоторой окрестности этой точки. Найдем предел и значение функций в данной точке.

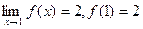. Видим, что 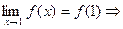функция у=f(x) непрерывна в точке х =1.

Для функции у=g(x), хотя функция определена в точке х =1, 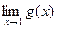не существует. Следовательно, функция у=g(x) не является непрерывной в точке х =1.

Функция у=f(x) называется непрерывной на промежутке (a; b), если она непрерывна в каждой точке этого промежутка.

Точки, в которых нарушается непрерывность функции, называются точками разрыва этой функции.

1. Основные теоремы о непрерывных функциях.

Имеют место следующие теоремы о непрерывных функциях:

Теорема 2.1. Пусть функции у=f(x) и у=g(x) непрерывны в точке х_о. Тогда

1. сумма или разность f(x)± g(x) непрерывны в точке х_о;

2. произведение f(x)·g(x) непрерывно в точке х_о;

3. при дополнительном условии g(x_о)≠ 0 частное f(x)/g(x) также непрерывно в точке х_о.

Теорема 2. 2. Пусть функция и=g(x) непрерывна в точке х_о, а функция у=f(и) непрерывна в точке и_о=g(х_о). Тогда сложная функция у=f(g(x)) непрерывна в точке х_о.

1. Свойства функций, непрерывных на отрезке.

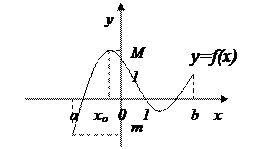Непрерывные на отрезке функции имеют ряд важных свойств. Рассмотрим одно из них.

Теорема 3.1 (Вейерштрасса). Если функция непрерывна на отрезке, тогда она достигает на нем своего наибольшего и наименьшего значения.

Рис. 10.3.

Изображенная на рисунке 10.3 функция непрерывна на отрезке [ a; b ]. Наибольшее значение М функция достигает в точке х_о, а наименьшее т – в точке а.

Для любого х 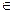[ a; b ] имеет место неравенство: т≤ f(x)≤ М.

Следствие. Если функция непрерывна на отрезке, то она ограничена на этом отрезке.

1. Непрерывность элементарных и сложных функций.

К непрерывным на области определения относятся все основные элементарные функции:

1. у=с, где с – const;

2. у=х ^α, где 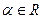- степенная функция;

3. у=а^х, где а >0, а≠ 0 – показательная функция;

4. у=log_ax, где а >0, а≠ 0 – логарифмическая функция;

5. у=sinx, у=сosx, у=tgx, у=ctgx – тригонометрические функции;

6. у=arcsinx, у=arcсosx, у=arctgx, у=arcctgx – обратные тригонометрические функции.

Всякие функции, которые получаются из основных элементарных путем выполнения над ними конечного числа арифметических операций или составления сложных функций называются элементарными функциями.

Все элементарные функции непрерывны на области определения.

Этот важный результат позволяет, в частности, легко находить пределы элементарных функций в точках, где они определены.

Пример 10.2. Найдите .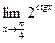

Решение. Функция 2 ^ctgx непрерывна в точке х = 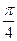, поэтому ее предел совпадает со значением функции в этой точке: .

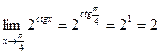1. Точки разрыва, их классификация.

Все точки разрыва функции подразделяются на точки разрыва первого и второго рода.

Точка разрыва х_о называется точкой разрыва первого рода, если в этой точке существуют конечные левосторонние и правосторонние пределы, т.е. 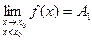и .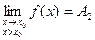

Если А₁ = А₂, то точка х_о называется точкой устранимого разрыва, если А₁≠ А₂, то точка х_о называется точкой конечного разрыва.

Точки разрыва первого рода можно представить следующим образом:

Рис. 10.4

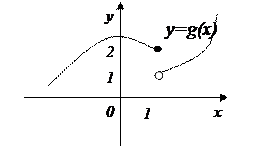
х =1 – точка разрыва I рода

точка устранимого разрыва точка конечного разрыва

т.к. 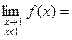т.к. и

Точка разрыва х_о называется точкой разрыва второго рода, если в этой точке хотя бы один (левосторонний или правосторонний) предел равен бесконечности.

Точки разрыва второго рода можно представить следующим образом:

Рис. 10.5

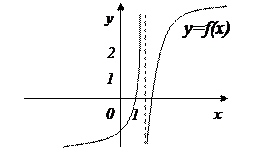
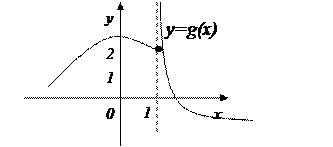
х =1 – точка разрыва II рода

т.к. 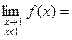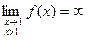т.к. и

Можно привести много примеров хорошо известных нам основных элементарных функций, имеющих точки разрыва второго рода:

· у= 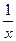, х =0 – точка разрыва II рода;

· у=tgx, х = 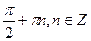– точки разрыва II рода;

· у=сtgx, х = 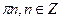– точки разрыва II рода.

Рассмотрим на примере, как находить точки разрыва функции и определять их род.

Пример 10.3. Найдите точки разрыва функции у= 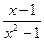и определите их род.

Решение. Функция у= 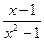является элементарной, следовательно, она непрерывна на области определения.

Найдем D (у): х² -1≠0; х ≠1 и х ≠-1. Получили, что точки х =1 и х =-1 являются точками разрыва функции. Для того, чтобы их классифицировать, найдем предел функции в указанных точках.

Для точки х =-1 , следовательно, х =-1 - точка разрыва II рода.

Для точки х =1

, следовательно, х =1 - точка разрыва I рода. Поскольку левосторонний и правосторонний пределы функции в этой точке совпадают, то х =1 – точка устранимого разрыва. Положив у= 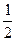при х =1, разрыв устранится, функция станет непрерывной.

График данной функции представлен на рисунке 10.6.

Пример 10.4. Найдите точки разрыва функции у= и определить их род.

Решение. Функция у= 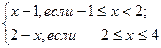состоит из двух частей: у = х - 1 (при 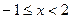) и у=2-х (при 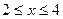). Функции у=х-1 и у=2-х являются элементарными, непрерывными на множестве R.

Имеет ли функция у= 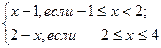разрыв? Она определена во всех точках отрезка [-1; 4]. Найдем левосторонний и правосторонний пределы данной функции в точке х =2.

Левосторонний предел: .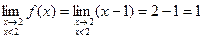

Правосторонний предел: .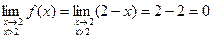

Рис. 10.7

Поскольку левосторонний и правосторонний пределы функции конечны, то х =2 – точка разрыва I рода. Но эти пределы не равны между собой, следовательно, х =2 – точка конечного разрыва.

График данной функции представлен на рисунке10.7.

Контрольные вопросы:

1. Когда функция называется непрерывной в точке х_о?

2. Что называют точками разрыва функции?

3. Какие точки называются точками разрыва I рода? II рода?

4. Каковы основные теоремы о непрерывных функциях?

5. Сформулируйте свойства непрерывных функций.

6. Какие функции являются непрерывными на области определения?

ГЛАВА 3.2. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ДЕЙСТВИТЕЛЬНОЙ ПЕРЕМЕННОЙ

Дифференциальное исчисление – один из важнейших разделов математического анализа, в котором изучаются производные и их приложения к исследованию функций.

Дифференциальное исчисление было создано сравнительно недавно, в конце XVII века. К этому понятию одновременно в 70-х-80-х годах XVII века независимо друг от друга подошли два величайших человека своего времени: английский ученый Исаак Ньютон (1643–1727) и немецкий математик Готфрид Вильгельм Лейбниц (1646–1716). Грандиозные успехи естествознания и математики в последующие три столетия были во многом определены великим открытием Ньютона и Лейбница.

Ньютон исходил из необходимости описывать движение тел и развитие различных процессов. Он мыслил как физик – кинематически. Для него суть дифференцирования – нахождение скорости тела в любой момент времени по известному пути. Свое открытие он сделал в 1665-1666 годах, когда Англию постигла эпидемия чумы, и Ньютон вынужден был находиться в своем поместье Вулсторп. Впоследствии он написал работу "Метод флюксий и бесконечных рядов", где метод флюксий – не что иное, как дифференцирование. Но эта работа была опубликована лишь в 1736 году. Сочинения Ньютона по математике увидели свет лишь в XVIII веке, однако кое-что было известно его коллегам из писем. Так, некоторые свои результаты в математическом анализе Ньютон сообщил Лейбницу в 1676 году, когда тот уже сам пришел к открытию дифференциального исчисления.

Подход Лейбница был геометрическим. На него большое впечатление произвели работы Паскаля, в особенности задачи о проведении касательной. В 1765 году им были сделаны первые шаги по созданию нового исчисления: в рукописях Лейбница появляются основные понятия, вводятся операции и символы. Именно Лейбниц ввел термин "дифференциальное исчисление", который с удивительной точностью описывает суть теории. Differentia по латыни – "разделение", "раздробление". Процесс дифференцирования состоит в замене функции на маленьком участке ее дифференциалом, т.е. кусочком ее касательной. Участку, на котором производится замена, Лейбниц дал название "бесконечно малый". Свои результаты Лейбниц опубликовал лишь в 1684 году в короткой статье из шести страниц "Новый метод максимумов и минимумов, а также касательных, для которого не служат препятствием ни дробные, ни иррациональные величины, и особый для этого род исчисления". С этого момента начинается официальная история математического анализа.

Следует отметить, что в предыдущие полвека Блез Паскаль (1623–1662), Пьер Ферма (1601–1665) и другие ученые фактически дали правила разыскания производных многих функций. Ферма предложил правила нахождения экстремумов. Ньютон и Лейбниц завершили это развитие, они разработали аппарат дифференциального исчисления до максимальных пределов, применили дифференциальное исчисление к решению многих задач геометрии и механики.

Исследования Лейбница в значительной степени определили развитие методов анализа в Европе. Среди его последователей – братья Иоганн (1667–1748) и Якоб (1654–1705) Бернулли, Пьер Вариньон и Гийом де Лопиталь (1661–1704). Именно Лопиталь в 1696 году стал автором первого печатного учебника по дифференциальному исчислению.

Дата добавления: 2014-12-27