Замечательные пределы. В курсе высшей математики рассматриваются несколько пределов, получивших название «замечательные»

В курсе высшей математики рассматриваются несколько пределов, получивших название «замечательные». Приведем некоторые из них:

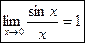- первый замечательный предел;

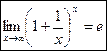- второй замечательный предел, аналогичный тому, что был рассмотрен нами в лекции 8, где х принадлежало множеству натуральных чисел.

Пользуясь этими формулами, можно вычислить ряд пределов.

Пример 9.9. Вычислите .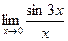

Решение. Поскольку под знаком синуса стоит угол 3 х, домножим числитель и знаменатель дроби на 3, чтобы выражение под знаком синуса и выражение в знаменателе стали равны: .

Вынесем число 3 за знак предела (следствие 1): .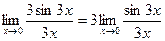

Применив первый замечательный предел, получим, что .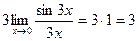

Ответ: 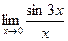=3.

Пример 9.10. Вычислите .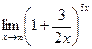

Решение. Постараемся преобразовать выражение под знаком предела таким образом, чтобы прийти ко второму замечательному пределу. Необходимо, чтобы числитель дроби был равен 1. Для этого разделим числитель и знаменатель данной дроби на 3; получим дробь вида: 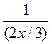. Теперь постараемся преобразовать показатель степени 5 х таким образом, чтобы в нем можно было выделить множитель (2 х /3). Для этого 5 х домножаем на 2 и 3 и делим на 2 и 3:

.

е

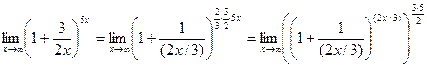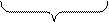Применив к выражению в скобках второй замечательный предел, получим, что .

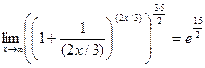Ответ: = .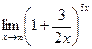

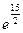Контрольные вопросы.

1. Что называют пределом функции 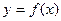в точке х_о?

2. Когда предел функции называют левосторонним? Правосторонним?

3. В каком случае функция имеет единый предел в точке х_о?

4. Какие свойства предела функции в точке существуют?

5. Можно ли утверждать, что неопределенность вида 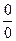равна 0? Какие приемы раскрытия данной неопределенности существуют?

6. Что называют пределом функци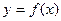и при →∞?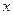

7. Какое правило для вычисления пределов функций при 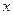→∞ существует?

8. Какие замечательные пределы Вам известны?

Дата добавления: 2014-12-27