Ряды распределения

Составной частью сводки и группировки материалов статистического наблюдения является построение рядов распределения.

Его цель – выявление основных свойств и закономерностей исследуемой статистической совокупности.

Статистические ряды распределения представляют собой упорядоченное расположение единиц изучаемой совокупности на группы по группировочному признаку:

а) Виды рядов распределения

Ряды распределения образованные по качественному признаку, называют атрибутивными. Например: распределение населения по полу, национальности профессии и т.д.

При группировке ряда по количественному признаку получают вариационные ряды.

При этом вариационные ряды по способу построения бывают (Рис. 21.):

- дискретными (прерывными), основанными на прерывнойвариации признака, например: тарифный разряд рабочих, число комнат в квартире, число детей в семье, число рабочих на предприятии и т.п.;

-

интервальными (непрерывными), основанными на непрерывно изменяющемся значении признака, имеющими любые, в том числе и дробные, количественные значения, например: заработная плата, стоимость основных фондов и т.д.

Рис. 21. Виды рядов распределения.

б) Характеристики рядов распределения

Вариационные ряды состоят из двух элементов: варианты и частоты.

Варианта – это отдельное значение варьируемого признака, которое он принимает в ряду распределения.

Частота – численность отдельных вариант или каждой группы вариационного ряда.

Частоты выраженные в долях единицы или в процентах к итогу, называются частостями, определяются:

, где

- частость;

- частота;

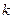- число групп.

Сумма частот составляет объём ряда распределения.

Самым первым шагом в упорядочении первичных данных при построении рядов является ранжирование, т.е. расположение всех вариантов ряда в возрастающем или убывающем порядке.

Ранжированный ряд данных позволяет сразу:

- увидеть наибольшее и наименьшее значение признака совокупности;

- определить расстояние между крайними значениями признака (размах вариации);

- выделить наиболее часто повторяющиеся значения в обследуемой совокупности (моду).

При построении интервальных рядов распределения необходимо установить число групп (К) и величину интервалов (i), на которые следует разбить все единицы изучаемой совокупности.

При группировке внутри однородных совокупностей применяются равные интервалы, величина которых зависит от вариации признака в совокупности (размаха вариации – R) и от количества обследованных единиц (n) и определяется по формуле:

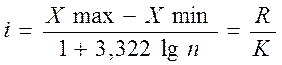
K=1+3,322 lgn – формула Стерджесса.

Указанное выражение почти всегда оказывается дробной величиной, которую округляют до целого числа, поскольку количество групп не может быть дробным.

А далее происходит образование групп обычным порядком. Точность величины интервала должна соответствовать точности исходных данных.

Нижнюю границу первого интервала целесообразно принимать равной минимальному значению признака.

При повторении интервальных рядов с непрерывными признаками возможно совпадение индивидуальных значений объекта с границами интервалов, возникает необходимость указать принцип образования групп:

(+) включительно;

(–) исключительно (см. стр. 23 настоящего учебного пособия.)

Для вариационных рядов с неравными интервалами необходимо для правильного представления о характере распределения рассчитывать:

- абсолютную плотность распределения:

;

- относительную плотность распределения:

;

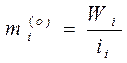Эти показатели используют для:

-сравнительной оценки различных рядов,

-перераспределения рядов, образуя новые интервалы.

в) Графическое изображение рядов распределения

Графическое изображение рядов распределения облегчает их анализ.

Для графического изображения дискретного ряда применяют полигон распределения.

Например: Имеются данные о распределении рабочих-сварщиков по квалификации (по тарифным разрядам) (Табл. 19.). Таблица 19.

Тарифный разряд (хi)	II	III	IV	V	VI
Число рабочих (fi)

Построим полигон распределения (Рис.22.):

Рис. 22. Полигон распределения.

Для графического изображения интервальных вариационных рядов применяется гистограмма.

При построении гистограммы вариационного ряда с неравными интервалами по оси ординат следует наносить показатели плотности интервалов (абсолютные или относительные) (Рис. 23.).

Например: Имеются данные о распределении магазинов по размеру товарооборота.

Таблица 20.

Группы магазинов по размеру товарооборота, тыс. руб.	Число магазинов	Величина интервалов, тыс. руб.	Плотность распределения единиц
	А			3=1:2
	До 50			0,5
	50-120			0,64
	120-250			0,5
	250-450			0,4
	450-980			0,04
	Итого:

Рис. 23. Гистограмма.

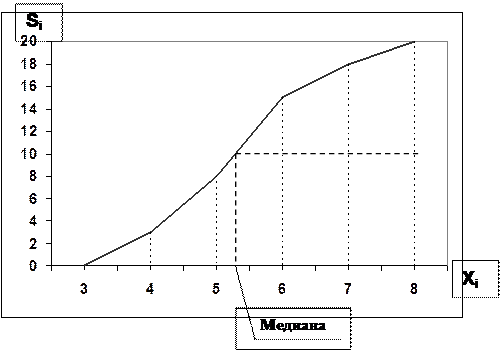
В ряде случаев для изображения вариационных рядов используют кумуляту (Рис. 24.).

Она строится на основании накопленных частот, которые откладываются по оси ординат.

Например, построим кумуляту по следующим данным:

Распределение коммерческих банков по размеру прибыли (Табл. 21.).

Таблица 21.

Размер прибыли, (xi), (тыс. руб.)	Число банков, (fi)	Накопленная частота, (Si)
3,0-4,0
4,0-5,0
5,0-6,0
6,0-7,0
7,0-8,0
Итого:

. Рис. 24. Кумулята.

По кумуляте можно определить медиану. Для её определения наибольшую накопленную частоту делят пополам, проводят прямую параллельную оси Х до пересечения с кумулятой. Абсцисса точки пересечения и будет медианой.

А при помощи гистограммы можно определить моду (Рис. 25.).

Например:

Рис. 25. Гистограмма.

Вопросы и задания

1. Что такое динамический ряд?______________________________________________________

__________________________________________________________________________________

__________________________________________________________________________________

2. В чем заключается различие между интервальным и моментальным рядом динамики?______

__________________________________________________________________________________

__________________________________________________________________________________

3. Как определить абсолютный прирост, темп роста, темп прироста, абсолютное значение одного процента прироста?____________________________________________________________

__________________________________________________________________________________

__________________________________________________________________________________

__________________________________________________________________________________

__________________________________________________________________________________

__________________________________________________________________________________

__________________________________________________________________________________

4. Существует ли взаимосвязь между базисными и цепными абсолютными приростами и темпами роста? Если «да», то какая? ___________________________________________________

__________________________________________________________________________________

__________________________________________________________________________________

__________________________________________________________________________________

5. Что такое ряд распределения?______________________________________________________

__________________________________________________________________________________

__________________________________________________________________________________

6. Как графически изображаются ряды распределения?___________________________________

__________________________________________________________________________________

__________________________________________________________________________________

Задание №9

Решите три задачи. При решении задачи 9.1. –Вы получаете отметку «удовлетворительно». Если будут решены две задачи (9.1. и 9.2.) –Вы претендуете на «хорошо», если же Вами решено верно все три задачи –Ваша отметка за практическую работу «отлично».

Задача №9.1

Валовой сбор картофеля в области характеризуется следующими данными: Таблица 22.

Год	Валовой сбор картофеля, млн. т.
	10,0
	12,0
	13,0
	10,0
	12,0
	12,0

Вычислите следующие показатели:

1) абсолютные приросты, темпы роста, темпы прироста; абсолютное содержание 1% прироста. Все показатели определите базисные и цепные. Полученные данные представьте в табличной форме;

2) докажите наличие взаимосвязи между базисными и цепными абсолютными приростами и темпами роста;

3) среднегодовой валовой сбор картофеля;

4) среднегодовой абсолютный прирост валового сбора картофеля;

5) среднегодовые темпы роста и прироста.

Задача №9.2

Остатки товаров в магазине составили (в млн. руб.) на 01.01-300; на01.02-310;на 01.03-260; на 01.04-260; на 01.05-270;на 01.06-280; на 01.07-300.

Определите вид ряда динамики. Вычислите средний остаток товаров по магазину за 1 квартал, за 2 квартал, за первое полугодие.

Задача №9.3

При изучении покупательского спроса на обувь зарегистрирована продажа следующих размеров женских сапожек: Таблица 23.

Для обобщения данных реализованного спроса постройте ряд распределения и проанализируйте полученные результаты, сравнив их с типовой шкалой поставки женских сапожек в магазин.

Типовая шкала поставки женских сапожек Таблица 24.

Размер									Всего
Число пар в % к итогу

Данные распределения покупательского спроса и типовой шкалы изобразите на графике. Укажите модальную величину ряда, распределения. Результаты разработок изложите в таблице, и сделайте выводы о соответствии предложения обуви покупательскому спросу.

Выводы:

Для достижения намеченных целей студентами было предложено:

-изучить материалы опорного конспекта, дополнить их личными примерами;

-ответить на вопросы для самоконтроля;

-выполнить практическое задание №9.

Дата добавления: 2014-12-23