Третій закон Кеплера

Обчислювальний експеримент

Алгоритм роботи

Добавимо до таблиці п’ять нових стовпців L, M, N, O, P. В них
будемо вносити результати обчислення сторін трикутника r_і, r_{і+ 1}, d_{і+ 1}, напівпериметра p_і і площі S_і.

Довжини всіх відрізків, як і раніше, обчислюємо за координатами їх початків і кінців. Уміст комірок таблиці має бути таким:

комірка	формули / числа
L3	=((E2)^2+(F2)^2)^0,5/1Е06
M3	=((E3)^2+(F3)^2)^0,5/1Е06
N3	=((E3-E2)^2+(F3-F2)^2)^0,5/1Е06
O3	=0,5*(L3+M3+N3)
P3	=(O3*(O3-L3)*(O3-M3)*(O3-N3))^0,5

Дільник 1Е06 = 1·10⁶ спрощує виведення результатів в таблиці.

На рис. 8.15 подано відповідний фрагмент доповненої таблиці:

	...	L	M	N	O	P
	...	Другий закон Кеплера
	...	rі	rі+ 1	dі+ 1	pі	Sі
	...	6,70	6,71	0,56	6,98	1,86
	...	6,71	6,73	0,55	7,00	1,86
	...	6,73	6,76	0,55	7,02	1,86
	...	6,76	6,81	0,55	7,06	1,86
	...	6,81	6,87	0,55	7,12	1,86
...	...	...	...	...	...	...

Рис. 8.15

Отже, перевірка другого закону Кеплера засобами обчислювального експерименту підтверджує його справедливість.

Завдання. Поверніться до рис. 8.10. У якому році – 1896 або 1874 – компонент меншої маси (тіло-супутник) рухався з більшою швидкістю?

Нагадаємо, що закони руху планет були встановлені І. Кеплером на основі вивчення даних із спостережень. На відміну від двох перших законів, де йде мова про особливості руху тіла-супутника (планети) відносно центрального тіла (Сонця), в третьому законі розглядаються дві довільні пари тіл, в кожній з яких тіла взаємодіють із силою всесвітнього тяжіння. У формулюванні Кеплера (для планет) квадрати періодів обертання будь-яких двох планет відносяться як куби їх середніх відстаней від Сонця:

.

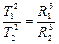Середньою відстанню R тіла-супутника від центрального тіла є половина великої осі орбіти – так звана велика піввісь.

Перевірку закону можна здійснити, маючи таблицю, побудовану для двох пар тіл («Сонце – планета1» і «Сонце – планета2»), або отримати його як теоретичний наслідок закону тяжіння, що ми і
виконаємо для найбільш простого випадку – для кругових орбіт.

Як було відмічено раніше, сила тяжіння надає прискорення обом тілам: 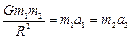, звідки

. (7)

З іншого боку 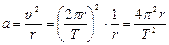, отже

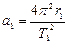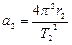; (8)

Об’єднуючи відповідні вирази з (7) і (8), отримуємо

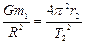; . (9)

Додаючи обидва рівняння з (9), і враховуючи, що Т ₁ = Т ₂, отримаємо

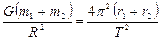або ,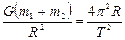

а це можна переписати у вигляді

.

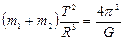Тут т ₁, т ₂ – маси тіл, що взаємодіють.

Переходячи до пари «планета – Сонце», отримаємо

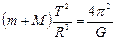= const.

Тоді для двох будь-яких пар тіл, в кожній з яких між тілами
діють сили всесвітнього тяжіння, можна записати:

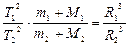(10)

Важко переоцінити значення виразу (10), що є уточненням третього закону Кеплера, що його виконав Ньютон на основі закону всесвітнього тяжіння Це одне з небагатьох співвідношень, які дозволяють порівнювати маси небесних тіл через інші параметри їхнього руху (в даному випадку через періоди обертання і радіуси орбіт).

Квадрати періодів обертання тіл-супутників навколо центральних тіл, помножені на суму мас відповідної пари тіл, відносяться як куби великих півосей їх орбіт.

Ще раз відмічаємо, що всі закони Кеплера описують поведінку будь-якої пари тіл, між якими діє сила всесвітнього тяжіння. Прикладами таких пар є Сонце – планета, Сонце – комета, планета – природний (чи штучний) супутник і тому подібне.

Дуже цікавими небесними об’єктами є комети, що мають вигляд хвостатих зірок або просто туманних плям, які переміщаються на тлі зоряного неба. Мабуть, найзнаменитішою періодичною кометою є комета Галлея. Записи про її появи можна простежити аж до 239 р. до н.е. Так її назвали на честь англійського вченого Эдмонда Галлея, який у 1705 р. першим припустив, що комети, які спостерігалися в 1456, 1531, 1607 і 1682 рр., були повторними поверненнями одного і того ж об’єкту. Він зробив передбачення, що комета знову повернеться в 1758 р., і її повернення, в 1758 р., вже після смерті вченого, довело, що вона є членом Сонячної системи. Коли комета Галлея
повернулася в 1910 р., Земля пройшла крізь її хвіст, що на той час стало джерелом надзвичайно сильного хвилювання серед населення, хоч проходження комети і не спричинило в природі ніяких наслідків. У 1986 р. спостерігалася чергова поява комети Галлея. Це було її сьоме і доки останнє повернення з подорожі навколо Сонця, якщо вести рахунок від тих днів в 1456 р., коли перелякані люди возносили молитви, благаючи захистити їх від «диявола, турка і комети».

Завдання

1. Отримайте вираз третього закону Кеплера для планет і Сонця (у формулюванні автора).

2. Обчисліть період комети Галлея.

8.4. Якщо у знаменнику закону тяжіння не r ², а r ^k

Далі мова піде про вивчення закону всесвітнього тяжіння для
довільного значення показника степеня k для відстані r між тілами

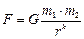(7)

Поставлену проблему можна сформулювати і так: як би рухалися тіла Сонячної системи, якби гравітаційна взаємодія відбувалася за законом тяжіння (7) при довільних k?

Така постановка проблеми виходить за межі шкільних курсів
фізики й математики і є об’єктом вивчення курсу теоретичної фізики. Тому дослідження комп’ютерної моделі виявляється єдиним методом, що дозволяє усунути ускладнення, пов’язані з обмеженим математичним апаратом школярів.

Дата добавления: 2015-01-03