Математична й комп’ютерна моделі

Перший закон Кеплера

Закони Кеплера як наслідки закону всесвітнього тяжіння

Закони руху планет були експериментально (шляхом безпосередніх спостережень) відкриті видатним австрійським математиком і астрономом Йоганном Кеплером на основі вивчення результатів тривалих спостережень за положеннями (координатами) планет (а точніше, Марса) на небесній сфері і подальшим представленням цих
координат у системі відліку, пов’язаній з Сонцем. Ці спостереження раніше виконав учитель Кеплера – голландський придворний астролог і астроном Тіхо Браге.

Як відмічають історики науки, для встановлення цих законів
Кеплеру довелося виконати дуже багато обчислювальної роботи. Кожне обчислення – три сторінки великого формату, а для запобігання помилок воно повторювалося 70 разів. Збереглося 900 аркушів таких обчислень, заповнених дрібним кеплерівським почерком. На ці розрахунки та на осмислення їх результатів учений витратив вісімнадцять (!) років.

Закон всесвітнього тяжіння був встановлений Ньютоном помітно пізніше, ніж закони Кеплера, і, як відомо, виявився їх теоретичним уточненням і узагальненням. Закони Кеплера були сформульовані тільки для планет, тобто для випадків, коли маса тіла-супутника (планети) набагато менша за масу центрального тіла (Сонця). Отже, з позицій закону тяжіння закони Кеплера передбачають тільки еліптичні орбіти, хоча, як ми бачили раніше, в залежності від початкових умов орбіта може бути однією з кривих другого порядку – колом, еліпсом, параболою чи гіперболою.

Закон всесвітнього тяжіння описує гравітаційні взаємодії будь-яких пар тел. Саме тому при перевірці законів Кеплера на основі
закону всесвітнього тяжіння ми скористаємося вже розглянутою
моделлю з еліптичною траєкторією – моделлю руху штучного супутника навколо планети.

Формулювання закону: Планети рухаються по еліпсах, в одному з фокусів яких знаходиться Сонце.

Визначення. Еліпсом називають геометричне місце точок, сума відстаней яких до двох заданих точок (фокусів) є величиною постійною.

На рис. 8.11 зображений еліпс. Тут показані: F1, F2 – фокуси еліпса; GH = 2 а – велика вісь; 2 b – мала вісь, C – центр симетрії.

Рис. 8.11

Зв’яжемо з еліпсом прямокутну систему координат, її початок помістимо в точку F₁, горизонтальну координатну вісь Х поєднаємо з великою віссю еліпса, а вертикальну вісь Y направимо вертикально вгору, як показано на рис. 8.11.

Внаслідок симетрії відносно точки С маємо F₂G = F₁H.

Окремим випадком еліпса є коло (фокуси співпадають і утворюють центр кола).

Суть пропонованого нижче підходу відтворює наступну ідею: якщо стверджується, що траєкторією руху є одна з кривих другого порядку, то всі точки такої траєкторії повинні задовольняти визначенню цієї кривої. На наш погляд, це надійний спосіб відрізнити еліпс від овалу або параболу від гіперболи – адже візуально вони
дуже схожі.

Те, що орбіта є еліпсом, зазвичай сприймається учнями на віру. Проте застосування комп’ютера дозволяє організувати дослідження, спрямоване на виявлення форми траєкторії.

Якщо траєкторія дійсно є еліпсом, а центральне тіло знаходиться у фокусі F ₁, то для всіх точок такої траєкторії повинна виконуватися щойно згадана рівність

r ₁ + r ₂ = 2 a = const.

Цей факт буде перевірений в обчислювальному експерименті.

Повернемося до таблиці на рис. 8.3, яка моделює рух штучного супутника Землі. Нагадаємо, що тут на основі закону тяжіння ми розрахували координати точок орбіти, які відповідають послідовним однаковим проміжкам часу Δ t, і за цими координатами побудували саму орбіту.

Відрізки r ₁ і r ₂ визначатимемо через координати x, у довільної точки М орбіти і координати фокусів F ₁ і F ₂

:

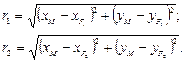
Відповідно до рис. 8.11 конкретизуємо значення деяких величин:

: х_{F 1} = 0, y_{F 1} = 0;

х_{F 2} = | x_max| – | x_min | = | x_max | – | x ₀|;

y_{F 2} = 0.

Після перетворення попередніх формул для r ₁ і r ₂ шляхом підстановки в них щойно встановлених значень отримуємо вирази, придатні для розрахунків:

;

.

Дата добавления: 2015-01-03