Уравнение в вариациях

В этом курсе нас больше всего будут интересовать вопросы, связанные с изучением систем управления, в которых основную роль играет обратная связь. Поэтому мы, пока хотя бы в общих чертах, познакомимся с природой обратной связи и с результатами, к которым приводит наличие ее в системе.

Предположим, что мы изучаем систему автоматического регулирования, структурная диаграмма которой приведена ниже:

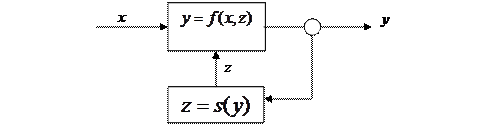
Пусть нам известны функциональные зависимости, связывающие входные и выходные параметры ОУ и управляемые переменные УУ, причем переменные x, y, z могут мыслиться как количества информации, поступающей и перерабатываемой ОУ и УУ.

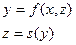
Пусть цель УУ – поддержание стационарного состояния ОУ в окрестности неподвижной точки (x ₀, z ₀, y ₀), т.е.

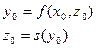
“Секрет” автоматического регулятора заключается в конструировании такого механизма, для которого желаемое значение регулируемой величины явилось точкой равновесия в фазовом пространстве и эта точка равновесия была бы аттрактором! Математическим оформлением этого факта служит понятие устойчивости и асимптотической устойчивости соответствующего решения (по Ляпунову).

Если сигнал (воздействие, стимул) на ОУ со стороны ОС изменятся и будет составлять не x ₀, а 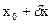, то УУ должно компенсировать это воздействие величиной, 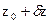так что величина 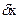должна быть как можно меньше! Так как

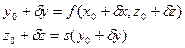
То

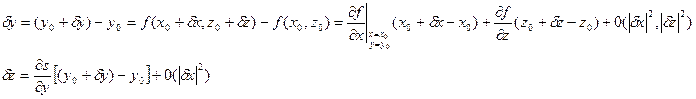
Поэтому в линейном приближении можно записать

,

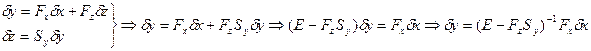где Е – единичная матрица.

Если же в этой системе управление «выключено», то было бы справедливо следующее соотношение

.

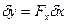Наличие обратной связи в регулируемой системе приводит к тому, что реакция системы 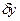на возмущение 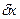оказывается «умноженной» на величину — оператор, обратный к (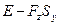), при этом величина 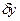(в соответствующей норме) тем меньше, чем меньше .

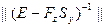Упростим ситуацию, и управление будем осуществлять в режиме компенсации, т.е. управляющее воздействие будем присовокуплять с сигналом х на входе ОУ.

Тогда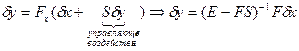

Замечание:

Конечно, наиболее эффективный случай управления в нашем примере – это случай полной компенсации возмущения со стороны ОС, т.е. 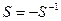, но он, естественно, в реальности труднореализуем, хотя бы потому, что он требует умения «предсказывать будущее», так как в реальности реакция запаздывает по отношению к воздействию на ОУ, а мы рассматриваем стационарную модель и время не принимаем во внимание.

Если совсем уж упростить ситуацию, то в качестве функциональных моделей (связь вход – выход) можно рассмотреть линейную пропорциональную связь, для которой 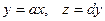и тогда будем иметь

.

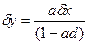Теперь выбор «системы» управления (СУ) заключается в подборе величины d, чтобы 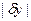принимал как можно меньшее значение. Если мы ограничены в выборе коэффициента пропорциональности d, например, условием 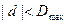, то мы естественно возьмем

,

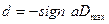что приведет нас к соотношению

.

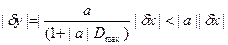Следовательно, наличие компенсаторной, пропорциональной обратной связи в УУ приводит нас к уменьшению в 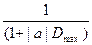раз возмущения со стороны ОС на ОУ. Обратим внимание и на тот факт, что коэффициент пропорциональности устройства управления противоположен по знаку коэффициенту a, т.е. компенсационная добавка 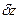противоположна величине 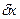, что согласуется с интуитивным представлением о компенсации как процессе. Компенсационное управление может принимать разнообразные формы. Например, повышая требования, предъявляемые к студентам на экзаменах, можно повышать одновременно им и размер стипендии. Примером компенсационного управления может служить и разнообразные системы страхования, широко используемые в обществе.

Мы рассмотрели эффект наличия обратной связи в общем случае и пришли к соотношению, связывающему небольшое воздействие со стороны ОС на ОУ с реакцией ОУ:

.

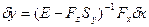Уже это соотношение, называемое «уравнением в вариациях» несет в себе некоторую информацию, позволяющую «создавать» системы управления с заданными свойствами («синтез» систем управления). Более подробно исследовать обратную связь начнем с изучения простейших механических систем, так как это самые простые системы из всех находящихся в нашем распоряжении. Говоря об их простоте, мы отмечаем, что их сравнительно легко изолировать от ОС, эти системы изучают уже давно (т.е. проблем с моделью ОУ у нас не будет) и, что не мало важно, эти системы линейны! Полученные результаты могут быть перенесены также и в другие предметные области с помощью системной аналогии.

Рассмотрим систему, функциональная схема которой приведена на рисунке. Пружина жесткостью К прикреплена к опоре вверху и может двигаться только в вертикальном направлении, что обеспечивается специальной конструкцией – кулисами без трения.

К нижнему концу пружины может быть приложена сила f (например, человеком), которая растягивает пружину. Это растяжение (равно как и сжатие) может регистрироваться (измеряться) с помощью указателя 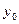, прикрепленного к пружине, и измерительной шкалы, жестко связанной с вертикальной стеной. Если на пружину не действует никакая сила (f = 0), то пружина находится в ненагруженной состоянии, и 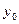соответствует нулю шкалы ( 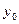= 0). Вообще говоря, силы, наблюдаемые в ОС, могут зависеть и от t – времени, что приведет к зависимости удлинение пружины 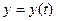. Далее мы будем пользоваться обозначениями f и y, а не 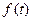и 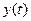, но при этом не следует забывать эту зависимость от времени. В терминах, принятых для систем, f – это входное воздействие (вход, стимул, причина, возмущение, вынуждающая сила), а y – ее выходная величина (выход, состояние, следствие, ответ, эффект, реакция и т.д.). Наша задача состоит в том, чтобы определить закон поведения (функционирования, эволюции) системы, связывающий обе эти величины между собой. Эта задача решается легко, если вспомнить закон Гука, в соответствии с которым сила f прямо пропорциональна растяжению y:

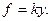(1)

Коэффициент пропорциональности называется жесткостью пружины и определяется свойствами материала, из которого пружина состоит.

Вообще говоря, существуют ограничения на применимость закона Гука – об этом хорошо известно материаловедам—реологам. В частности, если нагрузки на пружину очень большие, то вместо закона Гука следует использовать соотношение

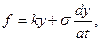
вытекающее из закона упруго–пластического течения или

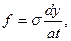
если деформации пружины принимать абсолютно–пластическими. То есть закон Гука – модель хорошо (адекватно) описывающая поведения пружины.

Но на эти детали при малых f мы сейчас внимания не обращаем!

Разрешим уравнение (1) относительно выходной величины:

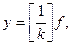(2)

в соответствии с причинно–следственной связью: f - причина, y - следствие. Это уравнение принято назавать уравнением “Вход - Выход”.Соотношение (2) может служить примером модели с пропорциональной зависимостью между входом и выходом. Это соотношение простое алгебраическое уравнение, при решении которого не возникает никаких проблем. Оно просто утверждает, что любому заданному значению входа f будет соответствовать единственное значение выхода y, вычисляемое по (2). Назовем множитель передаточной функцией системы, которую будем определять как величину выхода (y) к величине входа (f)

Исследуем теперь поведение y при различных характерах входного воздействия. Пусть это воздействие скачкообразно (кусочно-постоянно), т. е. при 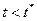равно f ₁, а при 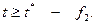Тогда мы получаем диаграмму поведения выхода системы

растяжение

t

t

передаточная   функция

сила

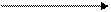
Отметим, что выход y повторяет (или как говорят специалисты по автоматическому управлению, отрабатывает) вход f мгновенно, без какого-то запаздывания. Подобные системы, описываемые алгебраическими уравнениями, назовем системами нулевого порядка. Если пренебречь разницей в природе величин f и y и рассматривать их как «сигналы», несущие информацию на входе и выходе, то можно подметить, что система изменяет лишь масштаб сигнала (умножает на некоторую постоянную величину), но не изменят его поведение во времени, т. е. формы или временной зависимости.

Добавим к пружине с указателем и шкалой еще один элемент – стрелку указатель y_i, не связанную с системой. Эта стрелка может свободно передвигаться вдоль шкалы произвольным образом. Предположим, что источником внешней силы, прикладываемой к пружине, является человек и он получил приказ все время поддерживать указатель y_о, жестко связанный с пружиной, на том же уровне, на каком находится y_i. какой схемой можно описать эту ситуацию? Наш человек (назовем его оператором) зрительно получает два входных сигнала: y_i – сигнал, подлежащий воспроизведению (задающий сигнал) и сигнал y_о – фактическое значение регулируемой величины. Функция оператора заключается в

1) сравнении этих сигналов

2) выработке (выбора) значения прикладываемой силы f_с, приложение которой к пружине изменила бы y_о так, чтобы «ошибка» y_о - y_i была устранена (скорректирована)

3) приложении силы f_с. Методом проб и ошибок эта задача решается достаточно просто, если, конечно, величина y_i не изменяется во времени

Обученный (тренированный) оператор решит эту задачу за сравнительно короткое время, необученный потратит времени больше. Теперь попытаемся исключить из нашей комбинированной пружинно – биологической системы человека и заменим последнего подходящим физическим устройством, конструкция которого на данный момент не имеет никакого значения! При этом будем предполагать, что пружина может испытывать возмущение (помеху) со стороны ОС силу Fd.

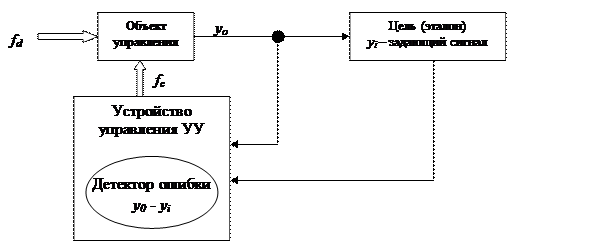
Например, это можно мыслить так, что наша конструкция находится в лифте или платформе с заметно неравномерным ходом. Жирные стрелки на схеме обозначают связь по силе, а тонкие – связь по информации.

Человека – оператора может заменить некоторое устройство, которое реализует вместо него следующие функции:

1) обнаруживает отклонение y_о от y_i - задающего сигнала,

2) вычисляет ошибку y_с = y_i - y_о (детектор ошибки),

3) вырабатывает управляющее воздействие f_с (какое – поговорим чуть позже),

4) прикладывает управляющее воздействие f_с к пружине (исполняет управляющее воздействие).

Детектор ошибки генерирует (порождает) сигнал ошибки y_с = y_i - y_о как разность между выходным сигналом y_о и задающим сигналом y_i. Выходной сигнал y_о нашей системы, необходимый для этой операции поступает в детектор ошибки по цепи обратной связи и, поскольку этот сигнал вычитается из y_i, обратную связь будем называть отрицательной. Исполнительная часть устройства управления (собственно регулятор) в качестве входного сигнала использует сигнал ошибки y_с и генерирует (порождает) управляющее воздействие f_с, прикладываемое далее к пружине – ОУ. В конкретном случае связь f_с и y_с может принимать различные формы (в зависимости от передаточной функции регулятора). Мы сначала изучим простейшую форму

f_с = k y_с, (3)

хотя эта простейшая связь может служить аппроксимацией более сложной зависимости, если она достаточно гладкая. Связь типа (3) между f_с и y _с будем называть пропорциональным регулятором, а величину k – коэффициентом усиления регулятора. Нетрудно понять, что самым лучшим выбором коэффициента усиления регулятора будет коэффициент жесткости пружины К – или как можно близкое значение k к величине К.

На схеме мы добавим еще один вход ОУ, связанный с воздействием на него ОС. Это воздействие носит, как правило, случайный характер и в большинстве случаев является причиной, по которой необходимо регулировать нашу систему.

Таким образом наша система, представленная схемой, может служить примером управляемой системы, называемой замкнутой системой автоматического регулирования с обратной связью. У этой системы задана цель, а именно: необходимость поддерживать выходной сигнал yо равным или по крайней мере близким к задающему сигналу yi в течение всей работы системы.Как помогает достижению этой цели наличие в системе обратной отрицательной связи? Если бы свойства и состояние ОУ не зависело от времени, то УУ могло выработать управляющее воздействие методом проб и ошибок, и обратная связь не потребовалась. Как мы уже знаем, такие системы называются разомкнутыми. Однако в реальности на систему действуют и другие силы, например случайные возмущения со стороны ОС, и более того, свойства ОУ не остаются строго постоянными по мере износа или исчерпания ресурсов. Основная задача системы автоматического регулирования (управления) может заключаться именно в том, чтобы поддерживать выход системы y_о равным (или очень близким) задающему сигналу yi (или уставке как он называется в технике), несмотря на такие изменения и воздействия. Единственным способом, посредством которого УУ может «узнать» о наличии таких возмущений состоит в наблюдении их воздействия на выходной сигнал ОУ, осуществляемый с помощью обратной связи. Поэтому замкнутые системы управления (с обратной связью) имеют гораздо большее применение в технике регулирования, чем замкнутые.

Если основная задача управления заключается в том, чтобы выходной сигнал системы «следил» за меняющимся задающим сигналом y_i= y_i(t), то такая система управления называется следящей. Если же основная задача управления заключается в том, чтобы выходной сигнал поддерживался равным или приблизительно равным постоянному задающему сигналу (уставке) y_i= const, то такая система управления называется регулятором. Примером системы первого типа может служить система управления противовоздушной обороны, а второго – карбюратор, терморегулятор инкубатора и т.п. Для того, чтобы разобраться в следующей системе управления добавим к пружине амортизатор,усилие которого определяется скоростью изменения растяжения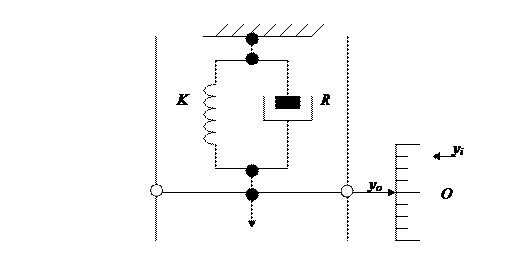

Тогда модель этой системы – модель ОУ примет следующий вид:

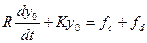(4)

где f_d – шум, а управляющее воздействие f_с осуществляется пропорциональным регулятором

f_с = k (y_i - y_о) (5)

Подобные системы управления, движения которых имеют первый порядок, назовем системами первого порядка. Введем ряд величин: 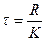- постоянная времени системы, , , 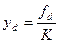то есть соотнесем все параметры системы к величине жесткости пружины К и введем псевдопеременные y_с и y_d как показатели управляющего воздействия и случайных возмущений среды. Тогда

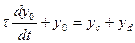(6)

Далее

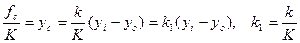(7)

Следовательно, модель ОУ (6) может быть переписана в виде

или

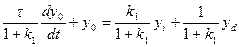(8)

Соотношение (8) назовем управлением движения системы с обратной связью. Это управление позволит нам проанализировать, какие свойства приобрела система при наличии обратной связи. Во-первых, порядок системы не изменился, во-вторых, постоянная системы (8) уменьшилась по сравнению с (6),

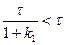(9)

что влияет на переходные процессы в системе. В третьих, при 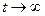имеем

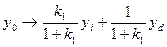(10)

Рассмотрим случай следящей управляющей системы, то есть 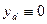(будем включать воздействие ОС в изменения сигнала y_i). Тогда

(11)

и эта погрешность (ошибка слежения) будет малой, если 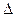будет мало, то есть чем больше 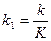, тем лучше!

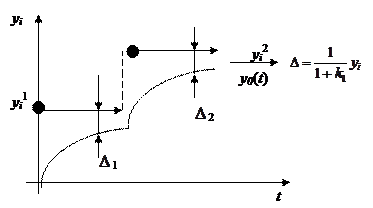
Рассмотрим случай системы регулирования, т. е. полагаем y_i= 0 и наша цель компенсировать возмущения ОС, т. е. y_d. Если предположить возмущения y_d ступенчатой функцией, то имеем 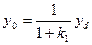и чем больше k ₁ тем лучше, так как задающий сигнал y_i= 0! Погрешность регулировки равна .

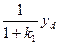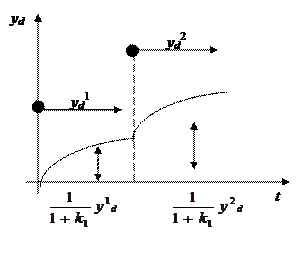
Таким образом, введение пропорционального управления приводит к появлению установившейся погрешности или ошибки, но в 1+ k ₁ раз меньше, чем была бы в системе без контура управления. Отметим также, что ошибка тем меньше, чем больше 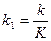. Наша задача будет заключаться в том, чтобы придумать управление с минимально возможной ошибкой.

Регулятор, задаваемый соотношением (5) называется пропорциональным или П-регулятором. Добавление контура пропорционального управления к системе первого порядка не изменяет вида дифференциального уравнения, описывающего систему в целом. Меняется лишь постоянная времени, что приводит к изменению переходных процессов и установившаяся погрешность в системе не устраняется.

Более интересна возможность изменения переходных процессов с помощью добавления контура управления к системе второго порядка, поскольку поведение системы в этом случае значительно богаче. К изучаемой системе добавим еще один элемент – массивный груз, что вносит в систему свойство инерционности:

Тогда уравнение движения системы примет вид:

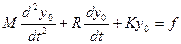(12)

Применение П-регулятора f_с = k_р (y_i - y_о) в контуре управления преобразует уравнение к виду

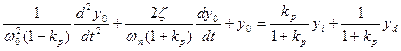, (13)

где приняты обозначения - собственная угловая частота и 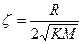- коэффициент затухания. В нашем случае, когда ОУ описывается системой второго порядка возможно использование не только П-регулятора, но и Д-регулятора (дифференциального), в котором управляющее воздействие определяется пропорционально скорости изменения ошибки

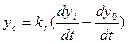(14)

Объединяя Д-регулятор с П-регулятором, получаем уравнение замкнутой управляемой системы при наличии ПД-регулятора:

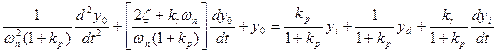(15)

Для анализа замкнутой управляемой системы, описываемой уравнениями (13), (15) необходимо вспомнить 10 фазовых портретов Линейной Динамической Системы 2 порядка. Рассматривая сначала П-регулятор (13), можно сделать следующие выводы, что введение П-регулятора

1) не изменяет порядок управления движения;

2) увеличивает собственную частоту системы ;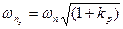

3) уменьшает коэффициент затухания

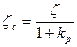(16)

Эффект увеличения собственной частоты является желательным, поскольку он увеличивает быстродействие системы. Однако уменьшение коэффициента затухания 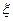может привести к возникновению (усилению) нежелательных колебаний. Установившаяся погрешность характерная как для задачи слежения, так и задачи регулировки уменьшается при увеличении k_p. Таким образом, если мы ограничиваемся только П-регулятором для ОУ описываемого системой второго порядка, мы приходим к противоречивым требованиям, которым надо удовлетворить при выборе наилучшего коэффициента усиления регулятора. Это требует выбора определенного компромиссного значения k_p. Однако совмещая П-регулятор с другими видами управления можно добиться лучших результатов. Анализ управления (15) описываемого ПД управления, замечаем что коэффициент затухания теперь выглядит так:

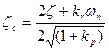(17)

Теперь с одной стороны мы можем выбрать коэффициент П-регулятора k_p достаточно большим, чтобы уменьшить установившуюся погрешность регулировки и с другой – за счет выбора коэффициента Д-регулятора k_r сохранить нужное значение коэффициента затухания. Вообще говоря, Д-регулятор, увеличивая коэффициент затухания системы, увеличивает устойчивость системы. Отметим, однако, что и Д-регулятор не устраняет установившуюся погрешность полностью, для чего нам надо было бы взять k_r >> 1. В заключении рассмотрим еще один тип управления, который устраняет эту установившуюся погрешность.

Этот тип управления называется интегральным.

При таком управлении сигналу ошибки пропорциональна скорость изменения управляющего сигнала (а не сам сигнал!)

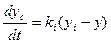(18)

Из (18) ясно, что управляющее воздействие y_c регулятора будет изменяться до тех пор, пока ошибка отличается от нуля. Происхождение термина «интегральный» становится ясным, если проинтегрировать (18) по времени, что дает:

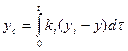(19)

или управляющее воздействие определяется как пропорциональное интегралу сигнала ошибки во времени. Интегральный регулятор как бы «запоминает» поведение ошибки во времени, и эта память, сохраняемая регулятором и после того, как сигнал ошибки стал равен нулю, позволяет поддерживать корректирующее воздействие, необходимое для компенсации сигнала ошибки (как тут не вспомнить злопамятного начальника, который все помнит). В этом состоит коренное отличие И-регулятора от П и Д-регуляторов.

Хотя И-регулятор можно применять самостоятельно, комбинированное ПИ управление обеспечивает обычно большее быстродействие системы и приемлемые пределы устойчивости. Управление ПИ-регулятора имеет вид

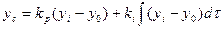(20)

Подставляя (20) в уравнение ОУ первого порядка получаем уравнение ОУ нового типа называемого интегрально-дифференциальным

(21)

Для избавления в (21) от интеграла достаточно продифференцировать его по времени:

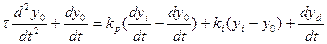(22)

и после некоторых преобразований приходим к уравнению замкнутой системы:

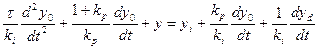(23)

Отметим два свойства уравнения замкнутой системы (23):

1. введение управляющего воздействия повысило порядок уравнения ОУ на единицу;

2. если y_i и y_d - ступенчатые функции, то их производные равны нулю и в установившемся состоянии y = y_i.

Заметим, что

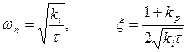(24)

Из чего следует, что при увеличении k_i растет собственная частота, а коэффициент затухания падает, увеличивая k_p мы увеличиваем коэффициент затухания при любых значениях k_i и следовательно нет смысла вводить Д-регулировку! В системах более высокого порядка это, вообще говоря, не так.

Следует обратить внимание на то, что использование И-регулятора в СУ наталкивает на трудности, связанные с «запоминанием» информации об ошибке. Использование компьютерных технологий в управлении снимает эти трудности. В «докомпьютерных» системах управления эта информация запоминалась в виде угла поворота закручивающейся пружины. Применение микропроцессоров в подобных устройствах позволяет исключить подобные проблемы.

Слово регулировать ассоциируется со словосочетанием «способность компенсировать со временем возмущения со стороны ОС» - математическим оформлением этого содержательного термина служит понятие «устойчивость».

Пусть динамическая система описывается системой обыкновенных дифференциальных уравнений:

x_i = f_i(t, x₁, …, x_n)

x_i(0) = x_i^o,

или записанная в «абстрактной форме»

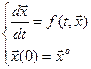
Решение 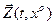будем называть устойчивым (по Ляпунову), если 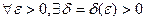такое что как только: |z₀ – x₀|≤δ(ε) то существует решение x(t, z₀) такое что

|x(t,z₀) – z(t, x^o)| ≤ ε.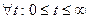

Следуя Ляпунову, решение z(t, x^o) назовем невозмущенным решением, а 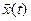- возмущенным.

Имеет место Теорема:

Для устойчивости решения z(t, x₀) линейной системы 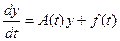при любом x₀ и при любой правой части f(t) где A(t) & f(t) непрерывные функции, необходимо и достаточно, чтобы тривиальное решение x(t)≡0 однородной системы было устойчивым.

Решение, не являющееся устойчивым, называют неустойчивым. Усилением понятия устойчивости является понятие «ассимптотическая устойчивость». Отражением важности этого понятия, как для теории управления, так и для других отраслей знание. Служит тот факт, что в математике используются и исследуются различные варианты этого понятия, такие как: равномерная устойчивость, устойчивость по части переменных, устойчивость на конечном интервале времени, абсолютная устойчивость, орбитальная устойчивость.

Возвращаясь к основному уравнению теории регулирования

δ = (E – F_zS_y)^-1Fx δx

связывающему возмущение движения управляемой системы δy с возмущением δx со стороны ОС обнаруживаем, что уравнение в вариациях не воспроизводит динамику процесса регулирования. Поэтому понятие устойчивости к нему неприменимо и необходимо функциональную зависимость выхода и входа системы (ОУ и УУ) исследовать как процесс, развивающийся во времени, то есть рассматривать ОУ и УУ как динамические.

В связи с этим нас будут интересовать так называемые переходные процессы в системах регулировки, возникающие при изменении режимов работы регуляторов. Принимая исходный режим и отождествляя его с нулевым состоянием можно получить следующие графики изменения показателя со временем с соответствующими названиями переходных процессов:

монотонный переходный процесс монотонно-логистический

процесс типа «ложного старта» процесс типа «овер-шут»

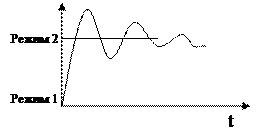
процесс типа «перерегулирование»

Рассматривая регулятор как управляемую систему, описываемую линейной динамической системой второго порядка, можно привести соответствующие условия на её коэффициенты, приводящие к тому или иному переходному процессу.

Дата добавления: 2015-01-03