Постановка общей задачи управления динамической системой

Нас будет интересовать управление системами, обладающими поведением. Под системой будем понимать совокупность элементов, находящихся в связях (причинно-следственных отношениях) и мыслимых как некоторое единое целое. Природа элементов может быть произвольна. Систему будем характеризовать своим состоянием в момент времени t [0, T ], которое будем описывать набором числовых величин-переменных состояния 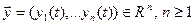зависящих от времени. Собственно под поведением и будем понимать изменение со временем этих величин (вектора состояния системы). Из курса системного моделирования мы знаем, что определение переменных состояния, составляющих исчерпывающее описание системы с точки зрения цели исследования, есть первый этап моделирования. Второй этап моделирования систем, обнаруживающих поведение, заключается в определение закона изменения этого состояния во времени. При этом время может быть как непрерывным (физическим), так и дискретным. Последнее можно трактовать так, что состояние системы можно наблюдать только в некоторые моменты времени, например такие 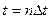, где n = 0, +1, +2,…, 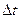- интервал между наблюдениями (стробоскопический метод). Мы в основном будем рассматривать непрерывное время, хотя с точки зрения компьютерной реализации дискретное время оказывается предпочтительным. Величину Т, ограничивающую промежуток времени наблюдения будем называть горизонтом. Горизонт может быть конечным, если нас интересует поведение (эволюция) системы за конечное время, или бесконечным в противном случае. Переменные состояния 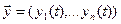могут быть действительными (вещественными), так и целыми, т. е. на y_i могут быть наложены некоторые ограничения. Например, если y описывает состояние склада (задача управления запасами), то естественно считать, что 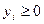, если y_i – число изделий i -го сорта.

Обозначим через y (t) – состояние системы в момент времени t. Если переменные состояния – действительные числа и их всего n, то 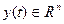. Таким образом исключаем из нашего рассмотрения так называемые «распределенные» системы, где состояние системы зависит от t и от точки пространства. Отображение 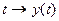описывает эволюцию, движение, поведение системы. Будем предполагать, что эволюция системы описывается некоторой моделью. Здесь возможны самые разнообразные ситуации. Модели могут быть детерминированными, со случайными факторами, с запаздыванием и т.п. Функция 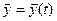в свою очередь может быть непрерывной – разрывной, регулярной (дифференцируемой) – нерегулярной (недифференцируемой) и т. д. Мы ограничимся только детерминированным и стохастическим случаями без запаздывания, приводящими к непрерывной функции состояния системы состояния системы y (t). В детерминированном случае модель чаще всего такова, что y (t) есть решение задачи для дифференциального уравнения с начальными данными:

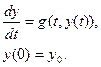(1)

Пример 1. Система чашка кофе описывается моделью

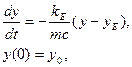
где y = y (t) – «средняя» температура системы, y₀ – начальная температура, y_E – температура окружающего чашку воздуха, принимаемой постоянной за время остывания кофе, k_E – коэффициент теплоотдачи, m – масса и с – удельная теплоемкость чашки кофе.

Пример 2. Народонаселение земного шара может быть описано с точки зрения динамики ее численности моделью

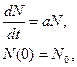
где N = N (t) – общая численность, a – коэффициент воспроизводства, N₀ – начальная численность населения Земли.

Если модель допускает «аналитическую реализацию», то мы можем определить функциональную зависимость y = y (t), как решение (1). В общем случае, когда аналитического решения нет или мы не в состоянии его определить, то (1) практически отражает факт изменения состояния системы между t и 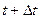, где 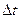- малый интервал между наблюдениями, как

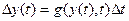(2)

где y (t) – состояние системы в текущий момент времени t. Так что состояние системы в момент времени 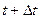описывается как

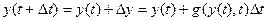(3)

Состояние (3) тем точнее, чем меньше 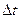. Такое свойство модели – способность описывать состояние системы в будущем будем называть прогностической функцией модели.

С состоянием (3) может быть связана и другая функция модели – объяснительная. При изучении системы мы можем высказать ряд гипотез и построить на их основе модель функционирования системы. Если она достаточно точно описывает наблюдаемое поведение системы, то мы можем с определенной уверенностью утверждать о справедливости высказанных гипотез. Если нет, то вернуться к высказанным гипотезам и подвергнуть их соответствующей модификации (по современному ре-инжинирингу) вплоть до удовлетворенного совпадения – адекватности.

Если при моделировании мы решили учитывать и случайные факторы, то изменение состояния системы 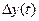будет уже случайной величиной. В этом случае естественно предположить, что к правой части (2) добавляются случайные поправки. При отсутствии информации о характеристиках случайных процессов (средние, дисперсия, закон распределения) проще всего предположить, что эта случайная поправка распределена по нормальному закону (как результат действия многих равномерно распределенных возмущений) со средним значением равным нулю и дисперсией, зависящей, в общем, и от y (t). Тогда, если две поправки, соответствующие двум не пересекающим интервалам времени независимы, в общем случае можно принять модель

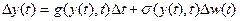(4)

где 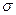- матрица, а 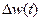распределено по нормальному закону со средним О и дисперсией 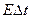(E – единичная матрица). Соотношение (4) представляет эволюцию системы в виде суммы двух процессов: детерминированного и случайного. Последний может представляться как описание воздействия на систему со стороны окружающей среды.

Важным моментом представления (4) является требование того, что 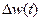для непересекающихся интервалов времен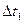и и 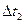были независимы. Это означает, что мы требуем, чтобы случайный процесс был Марковским, независимым от прошлого. Будущее системы будет определяться только его настоящим, так как мы решили процесс запаздывания не рассматривать. В этом случае достаточно предположить, что w (t) есть так называемый n-мерный Винеровский процесс и

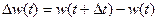(5)

Тогда требуемое свойство независимости от прошлого выполняется. Если 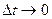, то в общем случае (4) можно записать в виде равенства дифференциалов

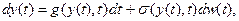(6)

а не в форме производных (1), ибо винеровский процесс, будучи непрерывным и имеющим ограниченную вариацию, не является дифференцируемым. Примером винеровского процесса является, например процесс броуновского движения частиц. Он находит широкое применение при анализе будущих изменений цен активов в финансовых задачах. Именно по этой причине он здесь и упоминается. Уравнение (6) называется стохастическим дифференциальным уравнением в смысле Ито. Решение уравнения (6) – непрерывный Марковский процесс, называемый диффузным процессом с приращением процесса g и матрицей 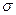- называемой диффузным членом. Если матрица 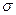невырождена, т. е. 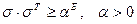, Е – единичная матрица, а неравенство понимается в смысле 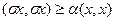для любого вектора 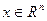, то dy (t), а значит и y (t), может принимать любые значения из Rⁿ с отличной от нуля вероятностью в силу того свойства закона нормального распределения. Это может вносить неудобства при описании содержательных ситуаций в ряде предметных областей, где на y (t) накладываются смысловые (содержательные) ограничения. Например, если y (t) есть некоторый запас, ресурс, то весьма желательно чтобы 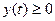. В этом случае модели (6) можно предпочесть диффузную модель с отражением

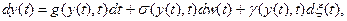(7)

где 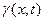вектор, который для точки 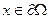( 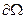- граница 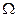- области изменения y(t)) направлен внутрь 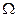, а 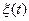- возрастающий скалярный процесс 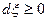, возрастающий лишь на границе области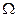 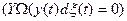. Иначе говоря, как только y (t) достигает границы 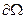, он испытывает постоянный скачок в направлении 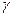на некоторую малую величину 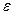внутрь области 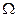. Конечно такой процесс не является непрерывным, но в пределе 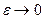получаем непрерывный процесс.

Приведенные выше модели естественно являются моделями без управления. Теперь мы опишем способы, которыми мы можем влиять на эволюцию системы.

Рассмотрим динамическую систему как кибернетический черный ящик. Если внешние факторы могут воздействовать на АС, то они это осуществляют через определение входа системы. Эти входы будем классифицировать на неконтролируемые и контролируемые (управляемые).

Пример: имея целью полета самолета конкретный пункт посадки следует принимать во внимание боковой ветер, способный сносить самолет с заданного курса. На этот фактор летчик влиять не может, он может лишь компенсировать его с помощью поворота горизонтального руля. Поэтому боковой ветер может представляться как неконтролируемый вход. Скорость полета самолета является контролируемым входом, так как летчик может увеличить подачу топлива в двигатель и, тем самым, увеличить скорость полета.

Под термином «вход» можно понимать определенное состояние внешней среды и внешних факторов по отношению к ДС, на которые система реагирует каким-либо образом. Состояние системы, которое в свою очередь воздействует на внешнюю среду или на положение ДС относительно цели будем понимать как «выход» динамической системы.

Выделяя и описывая состояния входов и выходов – каналов связи ДС с окружающей средой, мы решаем задачу обособления ДС от окружающей среды. Если мы адекватно решили эту задачу, то изменение состояния системы (показателей состояния) может произойти из-за:

1. изменения состояния входов системы,

либо

2. эволюции системы за интервал наблюдения.

Число входов и выходов можно пересчитать, а их состояния выразить в определенны

х числах. Если система имеет один вход и один выход, то мы будем их обозначать как x, y. В противном случае, поскольку состояние каждого входа и каждого выхода определяется одним числом, то состояние всех n входов и m выходов можно определить посредством задания векторов x = (x ₁, x ₂, …, x_n) и y = (y ₁, y ₂, …, y_m). В ряде задач выходы y ₁, y ₂, …, y_m могут мыслиться как параметры состояния системы, но в общем случае это не так.

Пример: инспектора по соблюдению санитарных норм интересует не температура воздуха в помещении как таковая, а вопрос «снижается ли эта температура ниже порогового значения?». Только в этом случае он должен принимать меры.

Если ставим задачу управления системой, т.е. оказание такого на нее воздействия, которое вызывает желаемое для нас изменение ее состояния, то ко множеству управляемых выходов в систему присоединим такие ее свойства, на которые мы можем оказывать влияние и изменять их.

Пример: угол поворота передних колес автомобиля относительно направления движения, скорость движения автомобиля или скорость полета самолета, доля ВВП расходуемого на потребление или накопление.

Далее управляемые входы (и свойства) будем обозначать как u = (u ₁, u ₂, …, u_n), если не оговорено противное.

Возвращаясь к модели эволюции ДС, мы рассмотрим два вида управления – непрерывное и импульсное. В случае непрерывного управления, вообще говоря, предполагается, что функция g - приращение процесса зависит не только от состояния y и времени t, но и от управления u, а именно

g = g (y (t), u, t)

Диффузионный член σ тоже, вообще говоря, может зависеть от управления.

Под управлением будем понимать процесс, задаваемый СУ (или УУ, ЛПР, ЧПР…) как значение, зависящее от t и от располагаемой в этот момент информации о состоянии ДС. То есть u = u (t) либо u = u (y(t)). В первом случае будем говорить о «непрерывном программном управлении», во втором о непрерывном управлении, реализующем принцип обратной связи. В общем случае значение управления u должно удовлетворять некоторым ограничениям типа u Є V_d, где V_d – допустимое множество управляющих воздействий.

Пример. Ограничение скорости, развиваемой данным транспортным средством либо правилами дорожного движения, на котором студент спешит на лекции по ТУ.

Если СУ (или УУ) имеет возможность наблюдать эволюцию ДС y (t) на протяжении всего времени (не предугадывая, естественно, будущего), то будем говорить, что наблюдаемость полная.

Итак, в случае непрерывного управления модель ДС записывается в виде

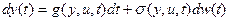(8) (8)

В импульсном управлении предполагается, что состояние системы в некоторые моменты времени (моменты управления) испытывает скачки (импульсы). Эти моменты времени и величина, интенсивность импульсов, их число являются переменными, подлежащими определению. Именно совокупность этих величин и будем называть импульсным управлением.

Итак, пусть 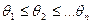- есть последовательность моментов управления, а 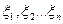последовательность соответствующих импульсов, тогда эволюция состояния системы описывается следующим образом:

если 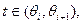, то

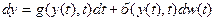
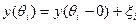(9)

,

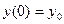где 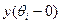есть величина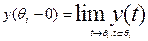

или 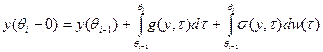(10)

Моменты управления 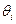и импульсы 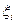могут выбираться как функции располагаемой информации к текущему моменту t (импульсное управление по принципу обратной связи). В соответствии с терминологией, принятой в теории вероятностей, моменты управления 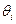можно называть еще и как времена останова. Разумеется, возможно одновременно и непрерывное, и импульсное управление.

В случае, когда на y (t) в силу содержательной постановки задачи наложены ограничения, например, y (t) может принимать только целые значения, то естественно Δ y (t) не может быть пропорциональным Δ t! В этом случае для Δ y (t) Є Z (множество целых чисел) можно задать его зависимость от текущего состояния y (t), приращения t и от управления. Например, в случае управления в задаче рождения-гибели, имеем:

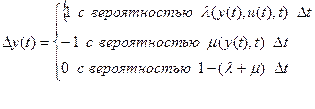(11)

Если этим процессом управляем импульсно, то имеем

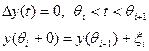(12)

где ξ_i может принимать только целые значения.

Приняв определенную природу модели – детерминированную или стохастическую, с непрерывным или импульсным управлением, с ограничениями или без них, нам надлежит идентифицировать функции и параметры, входящие в аналитическое описание модели. Пока этого вопроса мы не затрагиваем.

Цель управления в математической теории управления задается посредством формулировки критерия качества, подлежащего оптимизации (для определенности - минимизации), записываемого для детерминированного случая и непрерывного управления в виде:

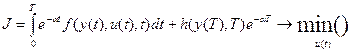(13)

где α - коэффициент актуализации (может быть равен нулю), T – горизонт управления, возможно равный +∞, функция f определяет интегральную «стоимость» управления, а функция h – «стоимость» конечного состояния ДС. Действительно, мы можем перейти к содержательной трактовке задачи управления. Тогда (13) может быть представлен в виде суммарной стоимости расходуемых ресурсов (массы, энергии, информации).

В случае импульсного управления критерий качества записывается в виде:

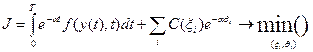, (14)

где 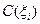- «стоимость», расходуемая на каждом импульсе.

Будем полагать, что 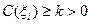, где k – минимальная стоимость импульса. Отметим существенное различие между случаями непрерывного и импульсного управления. В случае непрерывного управления «стоимость» управления, грубо говоря, «пропорциональна» промежутку длительности управления. В импульсном управлении, напротив, «стоимость» не пропорциональна (если f ≡0) длительности управления, а определяется числом импульсов и их интенсивностью.

Замечание.

Если в качестве допустимых функций рассматривать так называемые обобщенные функции – функционалы над S – множеством бесконечно дифференцируемых функций с конечным носителем, то существенная разница между непрерывным и импульсным управлением пропадает. Действительно, в этом случае импульсное управление реализуется линейной комбинацией δ - функций Дирака. С каждой интегрируемой функцией f может быть ассоциирована обобщенная функция – функционал, действующий по правилу:

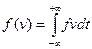
Рассматривая функцию

имеем, что хотя 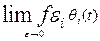в обычном смысле не существует, но для любой функции v Є S имеет место

,

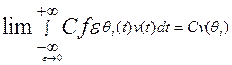то есть, как функционал над множеством S. Этот предел называется «δ- функция Дирака» и служит для описания импульсных процессов («сосредоточенных» величин).

Дата добавления: 2015-01-03