Принцип максимума Понтрягина

Понятие об оптимальном управлении.

Лекция 7. Управление динамическими системами.

Под задачей управления динамическими системами будем понимать следующую задачу: как найти допустимое управляющее воздействие приводящее динамическую систему в заданное состояние.

В качестве примера управления динамической системой рассмотрим управление движением материальной точки по прямой линии. Это может служить простейшей моделью движения автомобиля по прямой дороге. Под "заданным состоянием" будем понимать начало координат фазового пространства (пространства состояния динамической системы), в нашем простом случае фазовое пространство характеризуется двумя цифрами.

Уравнение движения материальной точки может быть записано с помощью второго закона Ньютона в виде:

(1)

где m- масса материальной точки, f - результирующая сил, действующих на точку. Эта результирующая, вообще говоря, может зависеть от положения точки x и её скорости dx/dt. Чтобы корректно сформулировать математическую задачу для дифференциального уравнения (1) надо добавить начальные данные

x(0)=a ₀, dx/dt(0)=a ₁ (2)

задающие положение и скорость точки в начальный момент времени. Теперь, если мы знаем силы, действующие на точку в произвольный момент времени, то задача (1) при (2) в математике называется задачей Коши для обыкновенного дифференциального уравнения и ее решение, если эти силы представляют собой кусочно-непрерывные функции, существует и единственно.

Задачей теории управления в данной ситуации служит выбор силового воздействия, такого, что под действием этого воздействия, точка из начального положения (a ₀, a ₁) за некоторое время T попадет в заданное состояние, а именно – начало координат.

В этом случае возможны различные постановки, связанные с управлением. Например, подобрать f так, чтобы переход в начало координат осуществлялся за минимальное время. Подобная задача в теории управления носит название задачи о быстродействии. Мы можем рассмотреть например задачу о максимуме пути, пройденном точкой за заданное время. Если мы введем функцию стоимости, связанную с состоянием динамической системы U(x,t), то может быть сформулирована и задача перевода динамической системы в заданное состояние с минимальным интегралом функции стоимости.

(3)

Вообще говоря, сформулированные нами задачи не являются независимыми, то есть решение одной задачи может являться и решением другой.

Перейдем от задачи (1) с начальными условиями (2) к эквивалентной постановке:

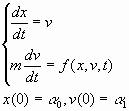(4)

Тогда для произвольного момента времени t, интегрируя уравнения движения,получаем:

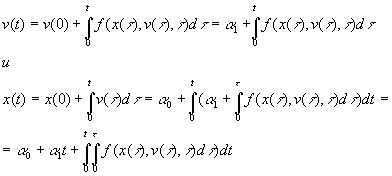
Первые слагаемые описывают влияние начальных данных на процесс движения, а слагаемые, содержащие интеграл определяются управляющими воздействиями, выбираемыми субъектом управления. Здесь и далее массу точки будем предполагать единичной.Таким образом, задача управления материальной точкой в нашем случае свелась к проблеме выбора управляющего воздействия f такого, что:

И при этом время Т должно принимать минимальное значение из возможного, если мы решаем задачу о быстродействии. Ограничим сначала сложность задачи. Будем предполагать, что управляющее воздействие - постоянная величина. Поставим вопрос так: можно ли в классе постоянных управляющих воздействий достичь заданного положения - начала координат? Далее управляющее силовое воздействие будем обозначать через u- как это принято в математической теории управления. Тогда, чтобы погасить скорость материальной точки за время Т, можно положить U= – a ₁/T. Вообще говоря, при больших значениях a ₁ и малых Т (мы ведь будем пытаться найти наименьшее значение искомого промежутка времени) могут отсутствовать технические возможности реализации такого управления. Действительно, тормозное усилие равно как и сила, ускоряющая движение автомобиля, не могут быть произвольными и ограничены техническими характеристиками двигателя транспортного средства. Поэтому далее будем предполагать, что на управляющее воздействие наложено ограничение |u|<=1. Тогда в качестве возможного управления может быть выбрано U= – signa ₁, которое за время Т, равное a _1¹ 0 погасит скорость материальной точки. Будем предполагать, что соответствующие величины должны быть приведены к безразмерному виду. Задача выбора управляющего воздействия будет нами решена, если будет выполняться условие

α0+α₁T+UТ² /2=0 (5)

означающее, что при прошествии времени Т=|a ₁| точка должна попасть в начало координат. Если начальная скорость a ₁ положительна, а начальное положение a ₀ отрицательно и удовлетворяет (5) то, прикладывая тормозную силу, за время Т=|a ₁| попадем в начало координат. Аналогично, если начальная скорость отрицательна, а начальное положение a ₀ положительно и удовлетворяет (5) то, прикладывая ускоряющую силу, за Т=-a ₁ попадем в начало координат.

Таким образом, если мы ограничиваемся постоянным управляющим воздействием u =-sign a ₁, то решить задачу можно, если начальные данные - положение и скорость движения материальной точки в начальный момент времени t=0, удовлетворяют условию (5). Если это условие отобразить в фазовом пространстве (x,v) в виде геометрического места точек LL', то получим решение задачи (без выяснения оптимума Т) только для точек фазового пространства, лежащих на LL'.

Теперь наша задача свелась к тому, чтобы научиться при любых (a ₀, a ₁) не обязательно удовлетворяющих условию (5) "попадать" как можно быстрее на эту кривую. Для этого посмотрим, что происходит с материальной точкой, если мы прикладываем к ней управление, противоположное по знаку скорости и равное единице по абсолютной величине. Нетрудно вычислить, что при U=+1 скорость и перемещение изменяются по закону

V (t)= a ₁+t => t=V-a ₁

x(t)= a ₀+a ₁t+1/2t² => x=V²/2+(a ₀ -a ²₁/2).

То есть точка фазового пространства, соответствующая текущему положению точки, движется по параболам, изображенным на рисунке, семейство которых определяется величиной C=a ₀ - a ²₁/2.

Аналогично можно установить, что в случае U= - 1 траектории в фазовом пространстве имеют вид x= - V²/2+(a ₀ -a ²₁/2). Вид этих траекторий наводит на мысль, что в качестве допустимого управления (управления, возможно решающего нашу задачу) может быть выбрано следующее. Если точка (a ₀, a ₁) находится "ниже" кривой LL' (а это имеет место для a ₀ + a ₁| a ₁| /2<0), то с помощью управляющего воздействия U=+1 перебираемся в точку кривой LL', из которой мы при U= - 1 уже попадаем в заданное положение – начало координат. Если точка начального положения находится "выше" кривой LL' в фазовой плоскости (если a ₀ + a ₁| a ₁| /2>0), то соответственно с U= - 1 перебираемся в точку кривой LL', из которой при U=+1 попадаем в начало координат. Кривую LL', при достижении которой материальной точкой нам приходится переключать управление, будем называть кривой переключения. Вычислим затраты времени, необходимые для реализации такого движения. Итак, если начальное положение и начальная скорость удовлетворяют условию a₀ + a₁|a₁|/2=0, то при U= - sign a ₁ мы за время Т= |a₁| добираемся до начала координат. Если a ₀ + a ₁| a ₁|/2<0, напр. в т. о, то нужно с управлением U=+1 "добраться " сначала в точку А, лежащую на кривой переключения LL':

Переключаем с U=+1 на U= - 1 и попадаем за время Т=| V_TA| в начало координат. Полное время движения будет определяться временем движения от точки О₁ до точки А и длительностью t=| V_TA|. Аналогично, если a ₀ + a ₁| a ₁| /2>0 (например в точке О₂) нужно с управлением U= - 1 добраться сначала в точку В, лежащую на кривой переключения, переключить управление с U= - 1 на U=+1 и попасть за время t₂=| V_TВ| в начало координат. Полное время движения будет определяться временем движения от точки О₂ до точки В и длительностью t₂. найдем полные времена движения.

Случай 1 a ₀ + a _{1| a 1|} /2<0, тогда сначала U=+1. Интегрируя уравнения движения от О до t при U=+1, имеем:

V(t)= a ₁+t

x(t)= a ₀+a ₁t+1/2t²

Определим момент достижения материальной точкой положения точки А. В точке А имеет место условие

x (t_А)+1/2 V(t_А) | V_TA| =0,

то есть

a ₀+a ₁t_А+1/2 t_А²+1/2 (a _{1 +} t_А) | a ₁₊t_A| =0,

что представляет собой квадратное уравнение относительно t_A:

_{a 1+}t_A=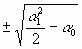

Так как в нашем случае a ₁₊t_A>0, то выбираем положительный знак радикала. Подкоренное выражение положительно в силу a ₀ + a _{1| a 1|} /2<0. Действительно, если a ₁<0, то a ₀ -1/2a ²₁<0, следовательно, 1/2a ²₁ - a ₀ <0, то есть -a ₀ -1/2a ²₁>0, но тогда и подавно 1/2a ²₁ - a ₀>-a ₀ -1/2a ²₁>0. Для момента времени t_A имеем:

V(t_А)= a ₁₊t_A= ,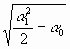

x(t_А)= a ₀+a ₁t_А+1/2 t_А²=1/2(a ₀ -1/2a ²₁).

Тогда полное время движения по траектории от точки О₁ до точки А и от точки А до заданного положения – начала координат – определяется как

Т=(-a ₁+ 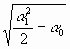)+| V_A(t)| = -a ₁+2 .

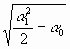Случай 2 a ₀ + a ₁| a ₁|/2>0, тогда сначала U= - 1. Интегрируя уравнения движения от точки О до t при U= - 1, имеем:

V(t)= a ₁ – t

x(t)= a ₀+a ₁t –t²/2

Аналогично определяем момент достижения материальной точкой точки В

x (t)+ V(t) | V_T|/2 =0 => t_B=a ₁ + .

В этот момент времени

V(t_В)= a ₁ – a ₁ = –

x(t_В)= a ₀+ a ₁(a ₁+ ) – 1/2(a ₁+ )²= a ₀+(a ₁ – 1/2(a ₁+ ))(a ₁+ )=

=a ₀+1/2(a ₁ – )(a ₁+ )=a ₀+1/2(a²₁ – a ₀+1/2a ²₁)=1/2a ₀+1/4a²₁=1/2(a ₀+1/2a ²₁).

Тогда полное время движения по траектории от точки О₂ до точки В и от точки В до начала координат определится как

Т=(a ₁+ )+| V (t_В) | = a ₁+2 .

Таким образом, мы определили допустимое управление, решающее задачу достижения точкой начала координат. Это управление заключается в следующем: в зависимости от знака величины a ₀ + a ₁| a ₁|/2 возможны четыре варианта выбора управляющего воздействия: два варианта без переключения (управление постоянно), либо два варианта с одним переключением (управление кусочно постоянно). Сделаем набросок некоего электронного устройства, управляющего движением материальной точки по принципу обратной связи. Представим себе, что мы в произвольный момент времени t обладаем информацией x(t) о положении материальной точки на прямой. Тогда, дифференцируя x(t) по t, нам будет известна и скорость V(t). Тогда функция управления U(t) может быть задана в виде U= –1signs, где s = x(t)+ 1/2 V(t) | V_T |. Устройство дифференцирования вычисляет величину скорости V=dx/dt по непрерывно наблюдаемому сигналу x(t), устройство F – формирует нелинейную величину 1 /2 V| V|, сумматор S суммирует входные величины x и 1/2 V| V|. Инвертор ^s формирует величину, противоположную по знаку величине s, пороговый ограничитель формирует U= – sign s, что служит управляющим сигналом для организации силового воздействия на материальную точку. Возможен и другой способ управления движением материальной точкой. Для этого способа характерно вычисление временных характеристик t_A или t_В, времен движения от точек А или В до начала координат к заданию управляющего воздействия в соответствии с временными рамками. Например, если материальная точка занимает начальное положение т. О₁, то управление, с помощью которого можно достичь начала координат, может быть определено как:

U(t) = 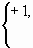при 0<t t_A = –a ₁+ 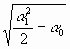, –1, при t_A<t –a ₁+2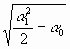

Или если материальная точка занимает начальное положение О₂:

U(t) = при 0<t t_В= a ₁+ , +1, при t_В<t a ₁+2 .

Если начальное положение и скорость точки находятся на кривой LL', то a ₀= a ₁| a ₁|/2, тогда U= – sign a ₁, 0<t | a ₁ |.Далее такой способ формирования управляющих воздействий будем называть "Автопилотом" или "программным способом". Как управление с помощью принципа управления обратной связи, так и программный способ можно просто реализовать с помощью управляющего алгоритма, выполняемого на компьютере в виде программы при наличии соответствующей информации. Для принципа обратной связи необходимо знание (x(t), V(t)), а для автопилота начальное положение материальной точки (a ₀, a ₁).

При выборе допустимого управления – алгоритма, определяющего u=u(t) в нашей задаче мы не касались вопросов оптимальности нашего управления. Под оптимальным управлением будем понимать такое управление, которое удовлетворяет заданному критерию качества. Выбор соответствующего оптимального управления дает теория оптимального управления, в частности принцип максимума Понтрячина, найденный Понтрячиным с коллегами, формулировку которого мы приводим ниже без доказательства.

Рассмотрим динамическую систему с законом движения

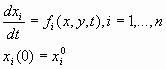
где x=(x1,x2,x3…) – фазовый вектор, однозначно определяющий состояние динамической системы, y- вектор внешних (входных) задающих и/или возмущающих воздействий, - фазовый вектор, задающий начальное состояние системы, t- время. Под управлением будем понимать такое воздействие u(t), с помощью которого можно достичь заданного состояния системы. Под оптимальным управлением будем понимать такое управление, которое удовлетворяет заданному критерию качества, например:

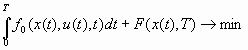
где x(Т) – возможное конечное состояние динамической системы в момент времени t=T. Вообще говоря, величина T может быть неизвестной и подлежащей определению. В задачах практики управление u не произвольно, а удовлетворяет ряду условий, ограничивающих ресурс управляющих воздействий, так что uÎ V, V -множество допустимых значений управления.

Для разрешимости исходной задачи и определенности будем рассматривать в качестве допустимых кусочно-непрерывное слева управление в точках разрыва

Согласно принципу максимума Понтрягина, алгоритм нахождения оптимального управления заключается в следующем:

1. Для каждого уравнения движения вводится двойственная переменная .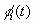

2. Стоится функция Гамильтона-Понтрягина

3. Составляются уравнения и краевые условия при t=T для сопряженных переменных

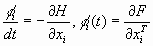
4. При фиксированных x, ψ, t, значения управляющих параметров u*(t) определяются условием

5. Из значений u(t), удовлетворяющих при каждом t предыдущему соотношению формируется управляющая траектория.

Принцип максимума является необходимым условием оптимальности. С его помощью можно сузить множество процессов x(t),u(t), претендующих на роль оптимальных. Подобная ситуация аналогична той, которая возникает при поиске минимума функции y=f(x), заданной на прямой. Если эта функция дифференцируема, то необходимым условием минимума функции в точке x* является равенство нулю производной в этой точке. Однако отсюда еще не следует, что в этой точке функция достигает наименьшего значения. Вообще говоря, наименьшее значение может и не существовать! Но при наличии дополнительной информации о функции может оказаться что условие df/dx=0 будет не только необходимым, но и достаточным. Например, если известно, что в окрестности точки x*.

Сейчас мы вернемся к задаче о быстродействии, рассмотренной нами в начале параграфа и применим к ней алгоритм принципа максимума:

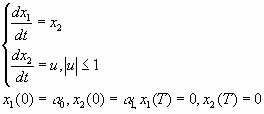
так чтобы .

Так как уравнений движения два, то вводим две двойственные сопряженные переменные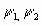

Строим функцию Гамильтона

Составляем уравнения, которым удовлетворяют сопряженные функции

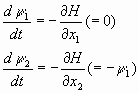
Ввиду того, что в функционале качества отсутствуют терминальные слагаемые и величина T не определена, условий на значение сопряженных функций нет! Решаем системы уравнений для сопряженных функций, находим:

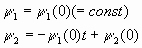
Определяем значения управляющих параметров u*(t) из условия

очевидно, что если выбрать 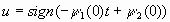, то H принимает максимальное значение.

Равенство 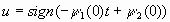определяет структуру управляющего воздействия. Из этого равенства следует, что возможны 4 варианта выбора управляющего воздействия – два варианта без переключения (u=const) либо два варианта с одним переключением в момент времени .

Эта структура совпадает со структурой управления, найденной нами эвристически – путем догадки. Значения управления по абсолютной величине равны 1 – максимальному значению из множества ограничений. Это обстоятельство может быть сформулировано так:”Если вы хотите достичь цели как можно быстрее, прилагайте как можно больше усилий”. Автор данного высказывания далее замечает, что “эта примитивная философия хотя не дает хороших результатов применительно к человеческим усилиям, но она приводит к хорошим результатам в системах управления”.

В качестве иллюстрации применения принципа максимума Понтрягина к управлению в экономических системах, рассмотрим задачу об оптимальном планировании. Рассмотрим замкнутую систему, состоящую из двух элементов – сектора А(производство продуктов производства) и сектора Б (производство продуктов потребления). Средства производства (фонды) в секторах будем считать однотипными и их количество в секторах будем обозначать за x₁, x₂. Примем за а коэффициент фондоотдачи, за m- коэффициент амортизации фондов. Тогда на основании баланса, можно записать:

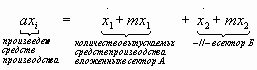
обозначим 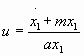- долю новых фондов, направляемых в сектор А. Управление в экономической системе будет заключаться в выборе величины 0<u<1 части средств, направляемых на развитие сектора производства средств производства. Тогда имеем:

начальное состояние экономики задано . Целью управления является максимизация выпуска предметов потребления за заданный период времени. Этот выпуск определяется функционалом:

Следовательно поставлена задача оптимального управления, для решения которой применим принцип максимума Понтрягина. Прежде всего заметим, что задача максимизации функционала эквивалентна задаче минимизации с подынтегральной функцией, взятой с противоположным знаком. Тогда функция Гамильтона имеет вид:

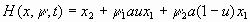
Уравнения, которым удовлетворяют сопряженные функции, имеют вид:

при конечных условиях 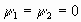. Тогда условие максимума функции Н при x=x(t), по параметру u дает закон:

Исследуем последний случай. Имеем ψ₂=T-t. Тогда и из уравнения для ψ₁ получаем -1=- a(T-t), что невозможно ввиду 0<t<T. Следовательно неопределенность u(t) возможна лишь для отдельных точек по t, что для дифференциальных уравнений не существенно. Следовательно оптимальное управление u может быть только кусочно-построенной функцией со значением 0 или 1.

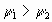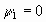Рассмотрим интервал постоянства управления, примыкающий к Т. пусть u(t)=1 на этом интервале. Тогда с одной стороны , а с другой из следует, что , при t=T. Поэтому С1=0 и , что противоречит условию 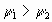. Следовательно u=0 на интервале [t,T] примыкающему к T. При этом 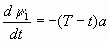, следовательно 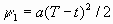, момент переключения управления определяется условием 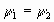следовательно

то есть τ=T-2/a. Переключение происходит если τÎ [0,T], или aT>2

пусть это условие выполнено и u=1 при s<t<τ. Νа этом интервале . Тогда интегрируя уравнение:

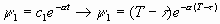
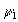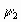рассмотрим разность функций и q=(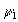 - 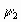). Дифференцируя это равенство, получим:

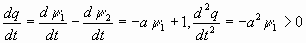
то есть функция q выпуклая. Из этого следует, что q(t)>0 при t< , то есть ₁(t)> ₂(t), а значит U(t)=1 при всех 0 t< и других точек переключений нет. Поэтому при выполнении условия aT>2 оптимальное управление имеет вид:

U(t) = при 0 t< , 0,при t T.

В противном случае переключений нет и U(t)=0, 0 t T.

Таким образом, в задаче об оптимальном планировании имеется единственная кусочно-постоянная функция, удовлетворяющая принципу максимума Понтрячина. Считая, что решение задачи в допустимом классе управлений существует, остается принять полученные управления за решение задачи. Вид оптимальной траектории легко получить, решив систему дифференциальных уравнений с найденной управляющей функцией.

Структура оптимального управления имеет простую …полическую интерпретацию. Если время планирования Т велико (аТ>2), то на первом этапе следует развивать сектор А, направляя в него все создаваемые фонды. После момента времени =Т-2/, все новые фонды направляются в сектор Б, производящий конечную продукцию. Если времени мало (аТ<2), то все фонды направляются сразу во второй сектор, производящий конечную продукцию.

Лекция 8. Динамическое программирование в задачах управления.

Метод ДП - один из наиболее мощных и совершенных математических методов современной теории управления - был создан в конце 50-х гг американским математиком Ричардом Беллманом. Этот метод для вас не нов. В курсе Методы оптимизациии вы рассматривали его и знаете в чем он состоит. Его применение к многошаговому процессу управления, а также многочисленные приложения метода к разнообразным проблемам теории принятия решения, экономики и других предметных областей способствовали закреплению этого метода как одного из важнейших инструментов теории оптимальных управляемых процессов.

Сформулированный Р. Беллманом принцип оптимальности гласит:

Отрезок оптимального процесса от любой его точки до завершения сам является оптимальным с началом в этой точке.

Этот принцип легко доказывается от противного в предположении существования оптимальных процессов. На основании этого принципа выводится основное функциональное уравнение Беллмана или соответствующее реккурентное соотношение, если ОУ описывается моделью с дискретным временем.

Рассмотрим управляемую систему, состояние которой в каждый момент времени характеризуется n-мерным вектором х с компонентами х₁,..., х_n. Предполагаем, что время t изменяется дискретно и принимает целочисленные значения 0,1,... Так, для процессов в экономике дискретным значениям времени могут отвечать дни, декады, месяцы или годы, а для процессов в электронных устройствах интервалы между соседними дискретными моментами времени определяются тактовой частотой этих устройств. Предполагаем, что на каждом шаге на систему оказывается управляющее воздействие при помощи m-мерного вектора управления u с компонентами u,..., u_m. Таким образом, в каждый момент времени t состояние системы характеризуется вектором х(t), а управляющее воздействие - вектором u(t). На выбор управления обычно бывают наложены ограничения, которые в достаточно общей форме можно представить в виде

u(t) U, t=0,1,...(1)

Здесь U - заданное множество в n-мерном пространстве.

Под влиянием выбранного в момент t управления (принятого решения) система переходит в следующий момент времени в новое состояние. Этот переход можно описать соотношением

x(t+1)=f(x(t),u(t)), t=0,1,… (2)

Здесь f(х, и) - n -мерная функция от n -мерного вектора х и m -мерного вектора u, характеризующая динамику рассматриваемой системы. Эта функция предполагается известной (заданной) и отвечает принятой математической модели рассматриваемого управляемого процесса.

Зададим еще начальное состояние системы

х(0) = х°, (3)

где х⁰ - заданный n -мерный вектор. Таким образом, многошаговый процесс управления описывается соотношениями (1)-(3). Процедура расчета конкретного процесса сводится к следующему. Пусть в некоторый момент состояние системы х(t) известно. Тогда для определения состояния х(t+1) необходимо выполнить две операции:

1) выбрать допустимое управление u(t), удовлетворяющее условию (1);

2) определить состояние x(t+ 1) в следующий момент времени согласно (2).

Так как начальное состояние системы задано, то описанную процедуру можно последовательно выполнить для всех t = 0, 1,... Последовательность состояний х(0), х(1),...часто называется траекторией системы. Заметим, что выбор управления на каждом шаге содержит значительный произвол. Этот произвол исчезает, если задать цель управления в виде требования минимизации (или максимизации) некоторого критерия оптимальности. Таким образом мы, приходим к постановке задачи оптимального управления.

ЗАДАЧА ОПТИМАЛЬНОГО УПРАВЛЕНИЯ

Пусть задан некоторый критерий качества процесса-управления (критерий оптимальности) вида

J= 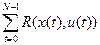+ F(x(N)) (4)

Здесь R(х, и) и F(х) - заданные скалярные функции своих аргументов, N — момент окончания процесса, N > 0. При этом функция R может отражать расход средств или энергии управляемой системой на каждом шаге процесса, а функция F- характеризовать оценку конечного состояния системы или точность приведения в заданное состояние.

Задача оптимального управления формулируется как задача определения допустимых управлений u(0), u(1),..., и(N-1), удовлетворяющих ограничениям (1), и соответствующей траектории, то есть последовательности х(0), х(1),..., х(N), которые в совокупности доставляют минимальное значение критерию (4) для процесса (2), (3).

Минимизация критерия (4) обычно отвечает выбору управления, обеспечивающего наименьшие затраты средств, ресурсов, энергии, наименьшее отклонение от заданной цели или заданной траектории процесса. Наряду с этим часто ставится также задача о максимизации критерия вида (4), например о максимизации дохода или объема производства. Однако нетрудно видеть, что максимизация критерия J эквивалентна минимизации критерия (-J). Поэтому простая замена знака у функций R и F в (4) приводит задачу о максимизации критерия к задаче о его минимизации. Далее всюду для определенности рассматриваем задачу о минимизации критерия (4).

Рассмотрим сначала элементарный подход к поставленной задаче определния оптимального управления. При помощи соотношений (2) состояние системы в каждый последующий момент времени выражаем через ее состояние и управление в предыдущий момент времени. Применяя это соотношение многократно, можно выразить состояния системы во все моменты времени только через начальное состояние х° и управления в предшествующие моменты. В результате получим из (4)

J=R(x0,u(0))+R(f(x0,u(0)),u(1))+ …=Ф(x0,u(0),u(1),…,u(N-1)).

Здесь Ф — некоторая громоздкая, но, вообще говоря, известная и вычисляемая функция своих аргументов. Таким образом поставленная задача оптимального управления свелась к задаче о минимизаций функции Ф от векторов u(0),u(1),u(t- 1), то есть от N переменных. При больших N (а обычно представляют интерес именно процессы с большими N), эта задача о минимизации функции большого числа переменных представляет трудности даже при использовании мощных компьютеров. Дополнительное осложнение вызвано тем, что переменные и(t) должны удовлетворять ограничениям (1).

Принципиально иной подход к поставленной проблеме дает метод динамического программирования.

Дата добавления: 2015-01-03