Связь с вариационным исчислением

Задачи определения функции, доставляющие экстремум (максимум, минимум, инфинум, супремум) выражению типа (15) в классической математике относятся к задачам вариационного исчисления. Выражения типа (15) представляет собой функционал. Вообще под функционалом будем понимать правило, ставящее каждой функции x (t) из некоторого множества, называемого областью определения функционала, число J [ x (t)], называемое значением функционала на функции x (t).

Пример:

Пусть L ¹[ t ₀, t ₁] - множество функций, интегрируемых на отрезке [ t ₀, t ₁]. Тогда

J [ x (t)] =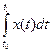

Является функционалом. А вот правило, ставящее каждой дифференцируемой функции y (t) ее производную, функционалом не является! Правило, ставящее функции ее производную называется в математике оператором.

В вариационном исчислении решаются задачи определения функций, доставляющих экстремум функционалам. Пусть, например,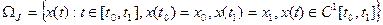

Тогда функционалом является выражение

J [ x (t)] = 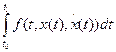, (18)

где принято обозначение .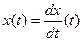

С помощью метода, широко применяемого в математике, а именно, сведением задачи к уже решенной, найдем условия, которым необходимо должны удовлетворять функции, доставляющие экстремум функционалу типа (18). Такие функции называются экстремалями функционала. Пусть имеется решение задачи – определение экстремали функционала (18), т. е. x ₀(t) – искомая экстремаль. Тогда рассмотрим семейство функций

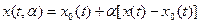(19)

зависящие от параметра α. Отметим, что x (t, α) Є Ω_J для любого α. Рассматривая теперь J α = J [ x (t, α)] как функцию от параметра α имеем

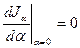
на основании того, что x (t,0) = x ₀(t) экстремаль! Тогда

=

= ,

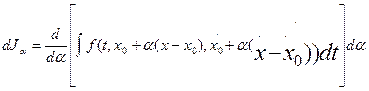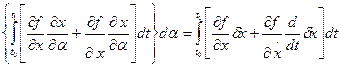где , ,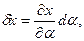

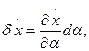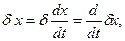
Далее

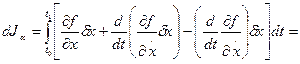
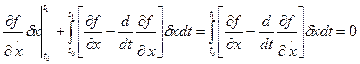
Окончательно приходим к необходимому условию экстремума функционала

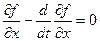
называемому уравнением Эйлера. Это уравнение является аналогом равенства нулю производной в точке экстремума для функционального исчисления. С помощью уравнения Эйлера может быть решена задача выбора траектории движения точки в вертикальном поле тяжести из т.А в т.В за наименьшее время. Это известная задача о брахистохроне.

Дата добавления: 2015-01-03