Принцип оптимальности

Сформулированный Р. Беллманом принцип оптимальности гласит: отрезок оптимального процесса от любой его точки до конца процесса сам является оптимальным процессом с началом в данной точке.

Принцип оптимальности легко доказывается от противного. Пусть х(t) = х* - некоторая точка оптимальной траектории, то есть состояние системы вдоль оптимального процесса в момент t, 0<t< < N. Рассуждая от противного, предположим, что отрезок этого процесса от момента t до момента N не является оптимальным процессом для системы (1), (2) в смысле критерия качества

J_t= 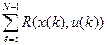+ F(x(N)) (5)

при начальном условии х(t) = х*. Значит, существуют допустимое управление u(t),.... u(N-1) и соответствующая ему траектория х(t +1),..., х(N), для которых критерий J_t из (5) принимает меньшее значение, чем на исходном оптимальном процессе. Наряду с исходным оптимальным процессом х(t), t = 0,1,… N. рассмотрим процесс, состоящий из двух участков: исходного процесса х(к) при k= 0, 1,..., t и "улучшенного" процесса х(t) при k= t+1,...,N. Для этого составного процесса критерий J из (4) будет иметь меньшее значение, чем для исходного процесса, так как сумма первых t слагаемых в (4) для составного процесса останется той же, что и для исходного процесса, а сумма остальных слагаемых, равная J_t, из (5), уменьшится по сравнению с исходным процессом. Данное утверждение означает, что исходный процесс не является оптимальным, а это противоречит сделанному предположению.

Таким образом, принцип оптимальности доказан. Столь простое доказательство наводит на мысль о тривиальности этого принципа. Однако это не так: принцип оптимальности является следствием аддитивности критерия оптимальности (4) и не имеет места в случае неаддитивного критерия. Более того, утверждение, кажущееся его обобщением:

“Любой участок оптимальной траектории является оптимальной траекторией” – вообще говоря несправедливо! Это просто установить, если рассмотреть забег спортсменов на дальнюю дистанцию.

Дата добавления: 2015-01-03