Прямая процедура

Воспользуемся результатами попятной процедуры для решения исходной задачи, то есть для построения оптимального управления и оптимальной траектории при заданном начальном условии (3). Полагая t = 0 и х = х°в (8), найдем управление в начальный момент: u(0) = v₀(х°). Далее из соотношения (2) определим состояние х(1) = f(х°, u(0)). Продолжая этот процесс, найдем u(1) = v_t(х(1)), х(2)) и т.д. Вообще имеем

u(t)=v_t(x(t)), x(t+1)=f(x(t),u(t)),

x(0)=x⁰, t=0,1,…., N-1 (9)

Соотношения (9) определяют прямую процедуру и позволяют полностью рассчитать оптимальное управление и оптимальную траекторию. Минимальное значение критерия оптимальности, отвечающее этой траектории, J= S(x°, 0).

Пример

В качестве примера рассмотрим модельную задачу об оптимальном функционировании фермы по разведению скота или птицы. Пусть х - число животных (или птиц) на ферме в начале некоторого интервала времени. Из этого числа их животных отправляется на продажу, а остальные животные приносят приплод, так что их число возрастает в q раз за рассматриваемый интервал. Уравнение (2) примет вид

x(t+1)=q[1-u(t)]x(t), t=0,1,...

Здесь q > 1 — постоянный коэффициент, и — управляющее воздействие (доля животных, отправляемых на продажу). Ограничение (1) в данном случае имеет вид 0 <=u<=1.

Расходы на содержание животных примем пропорциональными их оставшемуся числу и равными а[1 - u(1)]х(t) где а > 0 — постоянная; Выручку от продажи считаем равной сu(t)x(t), где с - цена одного животного на рынке. Поставим задачу максимизации дохода фермы за N шагов по времени. Как отмечалось выше, эта задача эквивалентна минимизации убытка (то есть дохода со знаком минус). Критерий оптимальности имеет вид (4), где нужно принять в соответствии со сказанным выше

R(x,u)=a(1-u)x-cux, F(х)=-сх. (11)

Последнее равенство (11) определяет (со знаком минус) стоимость животных на ферме в конце процесса. Учитывая соотношения (10) и (11), составим уравнение (6) для рассматриваемой задачи

S(x,t)=тin[а(1-и)х-сих+S(q(1-u)x,t+1)] (12)

0<=u<=1

Условие (7) с учетом (11) примет вид

S(x,N)= -сх (13)

Несложный анализ позволяет реализовать попятную процедуру и построить функции S(x,t) и соответствующие им управления из (9) для задачи (12), (13). Приведем окончательные результаты:

S(x,t)=a(q^N-1-1)(q-1)^-1x-cq^N-1 x

v_t(x)= 0 при a<c(q-1);

S (x,t)=-cx v_t(x)=1 при a>c(q-1) (14)

В том, что функции из (14) удовлетворяют уравнению (12) и условию (13) при всех t, можно убедиться методом математической индукции, проводя ее в сторону убывания t и начиная t=N.

Решения (14) допускают простую интерпрета­цию. Если а < с(q -1), то есть расходы на содержание животных сравнительно невелики, то имеет смысл не направлять животных на продажу (u) = 0) и получить наибольший доход, сохранив все поголовье к концу процесса. Если же а > с(q -1), то есть расходы на содержание велики, то целесообразно отправить на продажу сразу всех животных. В случае а = с(q — 1) оптимальное управление неединственно: в этом случае любое управление приводит к одному и тому же результату.

Более сложные и более содержательные результаты получим, если учтем зависимость рыночной цены с от числа продаваемых животных х (цена убывает с ростом х), а также зависимость расходов на содержание одного животного а от числа животных на ферме.

НЕПРЕРЫВНОЙ СЛУЧАЙ.

Рассмотрим далее случай детерминированной динамической системы с непрерывным управлением без ограничения на состояния

Управление u(t) выбираем из класса допустимых, так что u U и

где α - носит название "коэффициента актуализации", с математической точки введение этого коэффициента позволяет рассматривать случай когда T=+¥. "Экономическая" интерпретация этого коэффициента становится ясной, если учесть разный вклад величин f(t,u(t),y(t)) из-за величин t: сначала и предположить, например, если f=1, т.е., введение коэффициента α, называемого коэффициентом дисконтирования, позволяет описать инфляционные процессы. Определим функцию

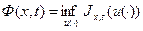
где функционал 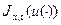зададим как значение целевой функции для динамической системы в момент времени t, занимающий положение x в фазовом пространстве если управление u(t) допустимо и известно.

Реализуем непрерывный аналог вывода реккурентного состношения принципа динамического программирования Беллмана. Пусть на отрезке 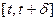, δ<<1 реализовано управление v(s), sÎ 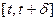Состояние y(t+δ) доступно наблюдению, тогда

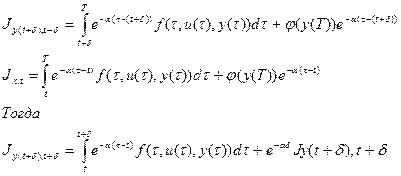
Пусть нам известно оптимальное управление u(s) с момента t+d

Тогда

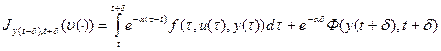
Теперь на основании принципа оптимальности Беллмана можно записать

Где нижняя грань определяется по функциям J(.), реализующим допустимое управление (гарантирующее переход системы из точки (x,t) в точку y(t+d) в момент времени t+d).

Разложим функцию Ф(y(t+d),t+d) по степени малого параметра d:

Вынесем из квадратных скобок величины, от υ не зависящие

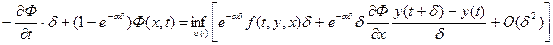Поделим на δ и перейдем к пределу при δ -> 0, тогда

Это нелинейное уравнение с частными производными называется уравнением динамического программирования или уравнением Гамильтона-Якоби-Беллмана. Здесь

мы воспользовались определением производной

для замены уравнений движения динамической системы. Привлекая условие Ф(T,x(T))=j(x(T)) получаем несколько необычную задачу для определения функции Ф(x,t):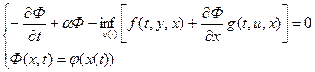

В математической теории оптимального управления устанавливается корректность этой задачи для функции Ф(x,t).

Построение алгоритма управления требует некоторого уточнения. Значение оптимального управления в каждый момент времени t есть правило (алгоритм) от имеющейся в этот момент информации. Если динамическая система наблюдаема, то к моменту времени t мы располагаем информацией о состоянии динамической системы и управлением во все предшествующие моменты времени. Будем называть управление обратной связью, если оптимальное значение управления в момент времени t зависит лишь от состояния ДС в этот момент, т.е. от y(t). Одним из основных результатов математической теории управления состоит в том, что при полной наблюдаемости ДС существует управление, которое является обратной связью.

В нашем случае (непрерывное управление динамическими системами) синтезируется следующим образом.

Пусть нижняя точная грань в скобках, где u,x считаются параметрами, реализуется на функции V(x,s) тогда оптимальное управление v(t) можно задать равенством:

v(t)=V(y(t),t)

Т.е. управление зависит от текущего состояния динамической системы и поэтому является обратной связью!

Если рассматривать непрерывное управление динамическими системами со случайными факторами, то уравнение Беллмана приводится к виду

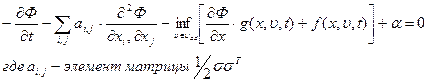
Случай импульсного управления. Рассмотрим случай детерминированной ДС с импульсным управлением, для простоты без ограничений. Здесь встает вопрос: когда нам выгодно осуществлять управляющий импульс и какова должна быть его интенсивность.

Функционал качества (критерий) целевая функция записывается в виде

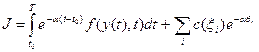
Рассмотрим сначала интервал (t,t+δ), свободный от управляющих импульсов. Тогда определяя функцию

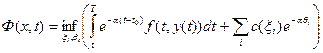
Имеем свободные движения на интервале t,t+ δ. При этом

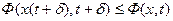так как нижняя грань берется по более широкому интервалу [t,T], а не [t+ δ,T]!

Тогда

(если t несвободна от импульсов, то <0!)

Пусть теперь в момент времени t система испытывает мгновенный управляющий импульс. Значит система из положения x перешла в положение x+x. До импульса была стоимость Ф(x,t) после стала Ф(x+x_it)+C(x). По определению Ф можем написать:

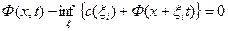Для свободной точки это условие !

А поскольку должно в любой момент времени tÎ[t,t+δ] реализовываться либо одно, либо другое, то одно из неравенств должно перейти в равенство, что можно записать в виде:

И к нему необходимо добавить конечное условие

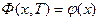
Таким образом импульсное управление ДС приводит к задаче не для дифференциального уравнения, а к задаче для неравенства, называемого вариационным!

Тематика импульсного управления интенсивно развивается. В частности есть обнадеживающие результаты в области управления производством электроэнергии, управления запасами, финансами, производством сырьевыми ресурсами, в задачах управления качеством с учетом износа, статистического управления в финансах, банковским портфелем (управление акциями), задачах распределения дивидендов в проблеме разорения.

Пример.

Применение импульсного управления к задаче терапевтического лечения.

Пусть X(t)- “уровень” болезни в момент времени t. В отсутствие лечения состояние больного эволюционирует согласно уравнению:

Рассмотрим последовательность моментов 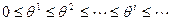в которые осуществляется лечение. Каждый акт лечения характеризуется его интенсивностью xⁱ. Пока продолжается лечение, состояние x(t) эволюционирует согласно уравнениям:

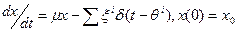
Однако лечение может оказать вредное воздействие на организм. Пусть y(t)-степень разрушения организма вследствие лечения. Тогда считаем, что состояние y(t) эволюционирует согласно уравнениям:

Где введены ограничения

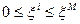
Предположим, что цель лечения состоит в удержании состояния x(t) в пределах 0£x(t)£x₀. Однако речь идет о том, чтобы чрезмерно не разрушать организм лечением, то есть 0£y(t)£y₀.

Пусть t - первый момент, в который x(t), или y(t) выходит из точки x₀ или y₀. Мы хотим максимизировать t. Учитывая стоимость одного акта лечения (равную k) ставим другую задачу минимизировать функционал

Где . Второе слагаемое есть цена лечения, производимого в момент .

Пусть 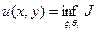, тогда эта функция является решением задачи

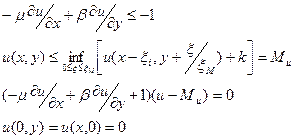
Отсюда можно вывести оптимальную стратегию лечения!

Решение конкретной задачи управления процессом лечения приводят к диаграммам, приведенным ниже:

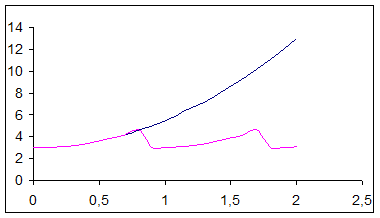
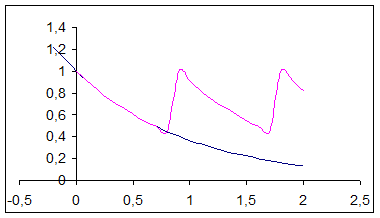
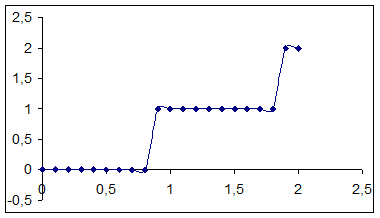
Предоставляем читателю в качестве небольшого упражнения разобраться что избражено на них (какие показатели состояния и в какие моменты проводится лечение).

Дата добавления: 2015-01-03