Сетевое управление в условиях риска

При вычислении продолжительности проекта считалось, что время на выполнение работ t(i, j) известно точно. В действительности это выполняется редко, как правило, сетевое планирование применяется для реализации сложных проектов, не имеющих аналогов и поэтому в качестве времени выполнения работ могут использоваться экспертные оценки. В ряде случаев длительности выполнения работ могут задаваться вероятностными законами распределения. Именно этот случай рассматривался в методе PERT.

Пусть длительность выполнения работы t(i, j) характеризуется средним значением 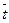(i, j) и дисперсией σ²(i, j). Априори предполагается, что вероятностное распределение продолжительности работ обладает свойствами:

а) непрерывности;

б) унимодальности (один максимум);

в) пересекает ось Ox в двух точках с неотрицательными абсциссами;

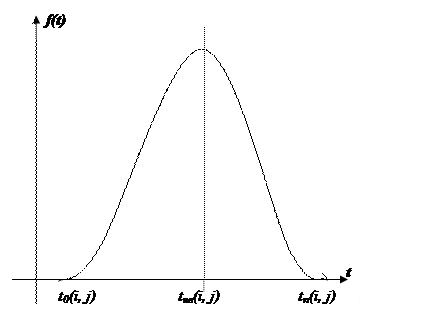
где f(t) – плотность вероятности, t₀ – оптимистическая, t_n – пессимистическая и t_нв – наиболее вероятностная оценка времени продолжительности работы (i, j).

Статистическая обработка большого количества реализованных проектов установила, что функция f(t) обладает положительной ассиметрией, то есть максимум кривой графика f(t) смещён влево относительно средней линии. Приемлемой моделью этого распределения принято считать β - распределение. На основании этого предложения можно воспользоваться довольно точными оценками:

или ,

.

Зная теперь { 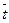(i, j)} и { σ²(i, j)} можно вычислить временные параметры сетевой модели и оценить надёжность – риск невыполнения проекта к указанной дате.

Оценка рисков невыполнения проекта в срок сводится к вычислению вероятности выполнения проекта к планируемой дате. Рассмотрим полный путь L, тогда, при условии, что он содержит достаточно большое число работ n≥12, по центральной предельной теореме, имеем:

,

и длительность выполнения всех работ, лежащих на пути L (составляющих путь L) будет случайной величиной, обладающей нормальным распределением с математическим ожиданием 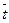(L) и дисперсией σ(L). Поэтому на основании свойств нормального распределения, имеем:

,

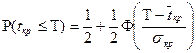где – вероятность того, что длительность критического пути не будет превышать длительности T, – среднее значение (оценка) длительности критического пути, – дисперсия критического пути, 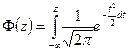– значение интеграла вероятностей Лапласа, 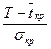– нормировка.

Считается, что если 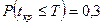или меньше, то опасность срыва заданного срока выполнения проекта велика. Необходимо предпринять дополнительные меры увеличения надёжности:

1. перераспределение исполнителей – наиболее опытных и поэтому надёжных на работе, составляющих критические пути;

2. пересмотр состава работ, а, следовательно, и сроков их исполнения;

3. перераспределение ресурсов и средств ресурсного обеспечения.

Если велика (0,75–0,8), то с достаточной степенью надёжности (с минимальным риском) можно прогнозировать выполнение проекта в установленный срок. В этом случае говорят о надёжности срока выполнения проекта – 75%-80% обеспеченности.

Для управления проектом представляет интерес и решение обратной задачи – определения срока выполнения проекта Т, который обладает заданной обеспеченностью в 100*β%. В этом случае полагаем: , где – нормированное отклонение случайной величины выполнения проекта, определяемого по функции Лапласа 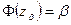. Для решения этого транцедентного уравнения можно воспользоваться таблицами: простыми или электронными.

Нами рассмотрены два типа сетевых графиков – с детерминированным и случайным временем выполнения работ. При реализации инновационных проектов приходится сталкиваться и с так называемыми стохастическими проектами. Для этих проектов список работ не определён и известен с некоторой вероятностью. На некоторых этапах тот или иной комплекс работ зависит от неизвестного заранее результата. В этом случае необходимо предусмотреть и проработать несколько вариантов продолжения реализации проекта в зависимости от полученных результатов на том или ином этапе стохастического проекта (точки бифуркации проекта). В любом случае необходимо использование технологии сетевого планирования и управления, так как вычисляемый срок реализации проекта представляет планируемое время реализации проекта и задаёт нам цель управления, то есть СПУ решает задачу целеполагания.

Сетевые графики

детерминированные сети случайные сети

определённые времена случайные времена определённые случайные

выполнения работ выполнения работ времена выпол- времена выпол-

нения работ нения работ

временные хар-ки оценка риска распределение временных

сетевого графика выполнения проекта характеристик сетевого графика

Под комплексным решением задачи целеполагания при управлении проектами будем понимать реализацию следующих шагов:

1. разбиение всего проекта на работы с указанием времени и последовательности их выполнения, соответствующих ресурсов (материальных, финансовых, оборудования, производственных мощностей) и исполнителей;

2. построение календарного графика, диаграммы Ганта, сетевого графика, исходя из списка работ, сформированного на первом этапе;

3. определение временных характеристик событий, работ, путей;

4. выявление критических работ, резервов времени событий, работ, путей;

5. оценка рисков выполнения проекта в срок, если проект недетерминированный;

6. анализ сетевого графика с точки зрения установления допустимого и возможного;

7. оптимизация сетевого графика.

При анализе сетевого графика будем проводить:

6.1 исследование сетевой модели на противоречивость;

Если при вычислении временных характеристик выявляются противоречия в списке работ и их последовательности выполнения, то противоречия в ресурсном обеспечении обнаруживаются на этом этапе.

6.2 установление целесообразности выбора работ – степени членения деятельности на работы;

6.3 классификация и группировка работ по величине ресурсов;

Рассмотрим подробнее пункт 6.3. Прежде всего необходимо заметить, что величина полного резерва работы связана с резервом максимального из путей L, проходящего через работу (i, j) и, следовательно, эта характеристика нелокальная! Величина R_п(i, j) не всегда достаточно характеризует степень напряжённости выполнения работы, лежащая на некритическом пути. Далее заметим, что работы, лежащие на критическом пути, резервов времени не имеют и запаздывание с их выполнением вызывает задержку выполнения проекта. Напряжённость в выполнении работы зависит от того, на какую последовательность работ распространяется вычисленный резерв, какова продолжительность этой последовательности работ.

Введём коэффициент напряжённости К_н работы (i, j), как отношения продолжительности несовпадающих отрезков пути, одним из которых является путь максимальной продолжительности, проходящей через данную работу, а другим – критический путь

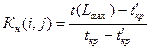
где t(L_max) – длительность максимального пути, проходящего через (i, j), t_кр – длительность критического пути, t^’_кр – длительность части рассматриваемого пути L_max, совпадающего с критическим. Необходимость вычитания величины t^’_кр объясняется тем, что резерв времени пути не раскладывается на часть критического пути, так как эти работы критического пути не имеют резерва. Имеет место

,

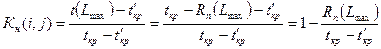где R_п(L_max) – полный резерв времени пути L_max.

Коэффициент напряжённости работы (i, j) может изменяться от 0 – если все работы, что не попали на критический путь, имеет длительность 0 до 1 для работ, лежащих на критическом пути. Следовательно, чем ближе К_н к 1, тем меньшим относительным резервом обладает максимальный путь, проходящий через данную работу (i, j).

Работы могут обладать одинаковыми полными резервами, но степень напряжённости сроков их выполнения может быть различна. И наоборот, различным полным резервам могут соответствовать одинаковые коэффициенты напряжённости. Зная величины коэффициентов напряжённости, можно дополнительно классифицировать работы по ценам. В критическую зону будем включать работы с коэффициентом напряжённости К_н ≥ 0,8, в подкритическую – 0,8≥К_н ≥ 0,6, в зону резерва – К_н (i, j)< 0,6.

Под оптимизацией сетевого графика понимается процесс улучшения организации выполнения проекта с учётом срока его выполнения. Понятие «улучшения организации выполнения проекта» требует уточнения. Под улучшением будем понимать сокращение длительности критического пути, выравнивание коэффициентов напряжённости и рациональное использование ресурсов, например, для людских ресурсов – уменьшение простоя исполнителей проекта. Сокращение продолжительности работ на критическом пути достигается с помощью:

1. перераспределения всех видов ресурсов с работ некритического пути (из зон резервных и подкритических) на работы критического пути (критические зоны);

2. сокращение трудоёмкости критических работ за счёт передачи части работ на другие пути, имеющие резервы времени;

3. параллельным выполнением работ критического пути;

4. изменением структуры сетевой модели – списка работ, сроков, ресурсов и т.д.

В идеале продолжительность любого полного пути должна стать равной длине критического пути или по крайней мере пути критической зоны. Тогда все работы должны вестись с равным коэффициентом напряжённости. Срок выполнения проекта в этом случае существенно сократится.

Под частичной оптимизацией сетевого графика будем понимать минимизацию времени выполнения проекта при заданной стоимости или минимизацию стоимости выполнения проекта при заданном времени выполнения проекта. Под комплексной оптимизацией будем понимать установление оптимального соотношения стоимости и сроков, в зависимости от конкретных целей.

Известна оптимизация сетевой модели методом «время-стоимость», в основе которого лежит предположение, что при уменьшении продолжительности работы пропорционально возрастает её стоимость, при наличии естественных ограничений

a(i, j) ≤ t(i, j) ≤ b(i, j)

где a(i, j) – минимально возможная (экстренная) продолжительность работы, b(i, j) – нормальная продолжительность работы.

Зависимость действительной стоимости работ от её продолжительности на отрезке [ a(i, j), b(i, j) ] аппроксимируем линейной зависимостью, тогда стоимость работы длительностью t(i, j) может быть вычислена, как

,

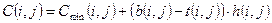где .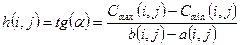

Величина h(i, j) носит название затраты на ускорение работы.

Очевидный вариант частной оптимизации – это использование резерва работ. Продолжительность каждой работы увеличиваем до тех пор, пока этот резерв не будет использован или пока не будет достигнуто верхнее ограничение b(i, j) на длительность. При этом стоимость выполнения проекта, равная до оптимизации , уменьшится на величину .

В реальных условиях может потребоваться ускорение выполнения проекта, что, естественно, приведёт к увеличению стоимости проекта. Поэтому необходимо определить зависимость между стоимостью проекта С и продолжительностью его выполнения С=С(t). В ряде случаев для оптимизации сетевых моделей проектов и для определения С=С(t) могут использоваться эвристические методы, основанные на экспертных оценках.

При линейной зависимости стоимости работ от их продолжительности задача построения оптимального сетевого графика проекта может быть сформулирована как задача линейного программирования, в котором минимизируется стоимость выполнения проекта при двух группах ограничений:

1. ограничение первой группы a(i, j) ≤ t(i, j) ≤ b(i, j);

2. ограничение второй группы требуют, чтобы продолжительность любого полного пути сетевой модели не превышала директивного срока выполнения проекта.

В заключение темы опишем командный цикл управления выполнения проектом с помощью методологии сетевого планирования и управления.

1. принятие решения об управлении выполнения проектом с помощью методологии СПУ (ЛПР, ГПР);

2. Решение задачи целеполагания для проекта (аналитик, сетевой оператор, эксперты, консультанты, руководитель проекта);

3. Контроль за выполнением проекта и сбор информации об отклонениях (времени и ресурсных) от цели – плана реализации части проекта (служба контроля, служба мониторинга);

4. Коррекция, повторение решения задачи целеполагания для оставшейся части проекта (аналитик, сетевой оператор, руководитель проекта);

5. Возврат к пункту 3, до тех пор пока проект не будет завершён (руководитель проекта принимает решение о перерасчёте временных и ресурсных характеристик).

Дата добавления: 2015-01-03