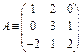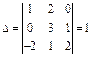Системы линейных алгебраических уравнений. Условие сущ-ния решения, решение систем по формулам Крамера и методом исключений, фундаментальная система реш-й

Определители. Определение и основные свойства (транспонирование, изменение порядка строк или столбцов, умножение на число, сложение строк или столбцов, разложение определителя по элементам строки или столбца). Вычисление определителей 2-го и 3-го порядков.

Пример

Пример

1. 
2. 
3. 
4. 

2. Метод исключения (на основе метода Гаусса)

Образуем систему линейных уравнений , (1)

АХ=У. (2)

X – неизвестные

Y – условно считаются известными.

По теореме Крамера система имеет единственное решение (так как )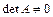

Для построения обратной матрицы систему (2) решаем методом Гаусса, т.е. методом последовательного исключения:

,

Х=ВУ,

С другой стороны, с учетом (2) Х= А^-1У. Так как решение единственно, то В= А^-1.

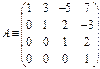
Составляем СЛАУ

х₄=у₄; x₃=y₃-2y₄; x₂=y₂-2(y₃-2y₄)+3y₄=y₂-2y₃+7y₄; x₁=y₁-3y₂+11y₃-38y₄.

Каждой матрице Аº(a_ij)_n´n по ниже следующему правилу ставиться число – который называется определитель соответствующей матрицы А.

Понятие определителя произвольного порядка можно ввести по индукции:

1) Если n=1 => Dºа₁₁.

2) Если n=2 => Dº 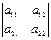ºа₁₁а₂₂ – а₂₁а₁₂₌ .

3) если таким образом уже введен определитель n-1 порядка, то определитель nго порядка называется

Dº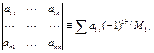

M_1j – det (n-1)-ого порядка (j=1,n).

!!!Отличие определителя от матрицы!!!

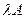– умножается вся строка

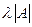– умножается одна строка или столбец

Свойства det:

1° При замене строк столбцами, т.е. при транспонировании величина определителя не меняется.

По правилу треугольника распишем и . Сравнивая результаты, получим, что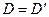

Это свойство устанавливает равноправность строк и столбцов => дальнейшие свойства достаточно сформулировать лишь для строк.

2° При перестановке любых 2-х строк определитель меняет лишь знак (доказательство на примере с правилом треугольника).

3° Если элементы 2-х строк равны, то det=0.

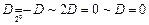
4° Общий множитель всех элементов некоторой строки можно вынести за знак det.

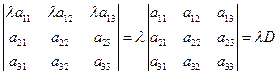
Доказательство – достаточно учесть, что в формуле треугольника каждое слагаемое содержит строго по одному элементу каждой строки и столбца. Следовательно, согласно правилу треугольника исходный определитель представляется в виде суммы шести слагаемых, причем каждое слагаемое обладает множителем l, который выносится за скобки, а в скобках – выражение, равное D.

5° Если все элементы некоторой строки = 0, то det = 0.

Доказательство – достаточно в 4° взять l=0.

6° Если соответствующие элементы 2-х строк пропорциональны, то det=0.

Доказательство – на основе 4° можно вынести коэффициент пропорциональности за знак определителя и по 3° det=0).

7° Если элементы некоторой строки представляют собой сумму 2-х слагаемых, то det может быть представлен в виде суммы 2-х det, у которых элементы рассматриваемой строки = соответствующим слагаемым.

Доказательство.

Рассуждения как в 4°.

8° Если к элементам некоторой строки прибавить элементы другой строки, умноженные на любое число, то величина det не изменится.

Доказательство:

(св-во 6,7)

T [Разложение det по строке]

Разложение по строке

Пр:

СЛАУ называется система n -го порядка: (1)

СЛАУ можно представить в виде матрицы АХ = В, где

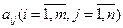– известные коэффициенты системы (1)

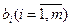– известные правые части системы (1)

– неизвестные (искомые) величины

· Набор 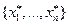(n -мерный набор) называется решением СЛАУ, если при подстановке их вместо соответствующих неизвестных каждое из уравнений системы превращается в истинное равенство (набор удовлетворяет (1)).

· Если система обладает хотя бы 1 решением, она называется совместной.

· Если имеется лишь единственное решение, то она называется определенной.

· Если имеется более 1 решения, то система называется неопределенной.

· Если нет ни одного решения, то она называется несовместной.

· Если решение одной системы является решением другой системы, то системы называются равносильными.

А – основная матрица, – расширенная матрица

Условия совместимости: Т. Кронекера-Капелли.

Система совместна (имеет хотя бы 1 реш-е) ó

Док-во: (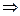) $ решение (2)

А имеет базисный минор r-го порядка. Любой столбец А представляется в виде линейной комбинации базисных столбцов. Перепишем соотношение (2) в виде:

–

линейная комбинация r базисных столбцов 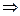максимальное число линейно независимых столбцов . Аналогично в обратную сторону.

Решение по формулам Крамера.

Метод применяется в случае квадратной СЛАУ: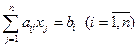

Если определитель , то система n -го порядка имеет единственное решение, которое дается в формуле Крамера (в терминах элементов): ,

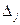– определитель, полученный из основного путем замены j -го столбца столбцом из правой части В.

Док-во:

(для n = 3) Умножим на и складываем правые и левые части:

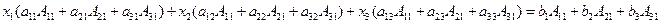
Аналогично для .

=> $ A^-1 => X=A^-1B – формула Крамера в терминах матричного представления.

Метод Гаусса (метод последовательных исключения).

Не обязательно det¹0, не обязательно квадратные матрицы. Расширенную матрицу приводим к треугольному виду с единицами на главной диагонали путем элементарных преобразований строк (не столбцов). Элементарные преобразования – 1) перестановка любых двух строк (столбцов); 2) умножение любой строки (столбца) на любое число, не равного 0; 3) умножение любой строки (столбца) на любое число и прибавление полученного результата к любой строке (столбцу).

На каждом этапе исключаются некоторые переменные (отсюда название метода).

И потом обратный ход: с конца подставляем решение в предыдущую строку.

Пример

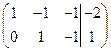– «укороченная» система

Дата добавления: 2015-01-03