
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Функция. ВП V называется n-мерным, если в этом пространстве $ хотя бы 1 линейно независимая система из n элементов
|
|
|
|
Предел
Базис
Размерность ВП
ВП V называется n -мерным, если в этом пространстве $ хотя бы 1 линейно независимая система из n элементов, а любая система из (n +1) элемента будет линейно зависима.
n называется размерностью и обозначается n = dim V
dim V = max число линейно независимых элементов
Пример 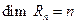
Система 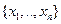 линейно независима, если
линейно независима, если 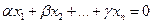 выполняется только когда все a,b,…,g=0.
выполняется только когда все a,b,…,g=0.
Если в V имеется любое число линейно независимых элементов, то оно называется бесконечномерным.
УТВ. dim V = n 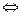 любые n линейно независимых элементов образуют базис этого пространства.
любые n линейно независимых элементов образуют базис этого пространства.
Пусть V – ВП
Система 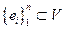 называется базисом этого пространства V, если она
называется базисом этого пространства V, если она
1) линейно независима
2) для 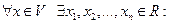
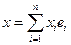
(любой элемент представляется как комбинация остальных элементов) – разложение элемента x по базису {ei} с координатами (x1,…,xn), которые определены только в данном базисе.
"xÎV, $! разложение, т.е. координата xi относительно базиса определяется однозначно.
Док-во: допустим имеется еще одно разложение 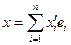
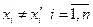
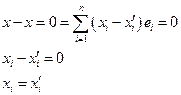
Получили противоречие, ч.т.д.
Пример 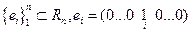 образует базис.
образует базис.
Численное значение базиса заключается в следующем: линейные операции над элементами сводятся к таким же операциям над обычными числами:
1) 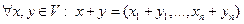
2) 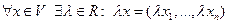
Евклидово пространство – вещественное векторное пространство, для которого:
1. имеется правило
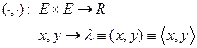
2. скалярное произведение подчинено следующим аксиомам:
1) (x, y) = (y, x) (коммутативность)
2) (x1 + x2, y) = (x1, y) + (x2, y) (дистрибутивность)
3) (lx, y)=l(x, y)
4) (х, х) = х2 >= 0,
если (х, х) = 0 => х=0.
Свойства ЕП
1° 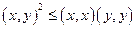 – неравенство Коши-Буняковского.
– неравенство Коши-Буняковского.
Пример.
1) V3- ВП всех геометрических векторов с обычным скалярным произведением 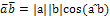 . В силу доказанных свойств скалярного умножения, 1-4 имеют место. => данное ВП явл. вещ. ЕП
. В силу доказанных свойств скалярного умножения, 1-4 имеют место. => данное ВП явл. вещ. ЕП
2) Rn со скалярным произведением 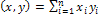 . 1-4 выполняется => Rn с указанным произведением является ЕП
. 1-4 выполняется => Rn с указанным произведением является ЕП
5. Пределы и непрерывность. Числовая последовательность и ее предел. Определение функции, ее непрерывность на языке "эпсилон-дельта" и языке пределов, равномерная непрерывность.
Если каждому значению n = 1,2,… ставится в соответствие по некоторому закону вещественное число xn, то множество занумерованных вещественных чисел x 1, x 2,…, xn,.. = { xn } называется числовой последовательностью. Это частный случай функции, аргумент которой принимает дискретные значения.
Если даны 2 последовательности { xn } и { yn }, то последовательность { xn + yn } называется их суммой, { xn * yn } – произведением, { xn / yn } для " yn ¹ 0 – частным.
Число A называется пределом последовательности при 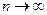
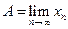 если " e>0 $ такой номер N 0>0: " n > N 0:
если " e>0 $ такой номер N 0>0: " n > N 0: 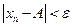
 |
В любой окрестности точки A находятся все члены последовательности, начиная с некоторого номера.
Если существует конечный 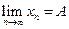 , то последовательность называется сходящейся. В противном случае (если A = ±¥ или lim не $) последовательность называется расходящейся.
, то последовательность называется сходящейся. В противном случае (если A = ±¥ или lim не $) последовательность называется расходящейся.
Точка x 0 называется предельной точкой множества M, если в " окрестности x 0 содержится бесконечное множество точек множества M.
Если последовательность имеет несколько предельных точек, то значение самой большой предельной точки называется верхним пределом последовательности 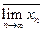 , а значение самой меньшей предельной точки называется нижним пределом последовательности
, а значение самой меньшей предельной точки называется нижним пределом последовательности 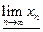 .
.
Пример.
1, 1-1/2, -1, 2, 1, 1-1/4, -2, 3, 1-1/8, -3, … n, 1-1/2n, -n, …
Последовательность имеет 3 предельные точки +¥; 1; -¥
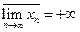 – неконечный, – неконечный, 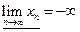 – неконечный.
Последовательность расходящаяся.
Последовательность может быть сходящейся, только если она имеет единственную точку (число).
Пример. {2-1/n,3+1/(2n)} нижний предел=2, верхний предел =3 – неконечный.
Последовательность расходящаяся.
Последовательность может быть сходящейся, только если она имеет единственную точку (число).
Пример. {2-1/n,3+1/(2n)} нижний предел=2, верхний предел =3
|
Последовательность называется ограниченной, если $ M >0, что для 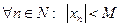
Т: Из всякой ограниченной последовательности можно выбрать сходящуюся подпоследовательность.
Т: Если последовательность сходится, то она является ограниченной. Обратное неверно.
Пример.
-1, 1, -1, 1, …, (-1) n – ограничена, т.к. 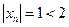 Но не сходится, так как 2 предельные точки
Но не сходится, так как 2 предельные точки
|
Если 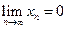 , то последовательность { xn } называется бесконечно малой.
, то последовательность { xn } называется бесконечно малой.
Если 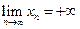 – бесконечно большой.
– бесконечно большой.
Связь неограниченная 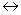 бесконечно большая: бесконечно большая Þ неограниченная
Неограниченный: для " M > 0 $ n 0Î N: | xn | ³ M
Бесконечно большая: для "e>0 $ N 0: для всех n > N 0: | xn | > e
n = N 0+1 | xn | > e º M Þ $n
бесконечно большая Þ неограниченная. Обратное не верно: бесконечно большая: бесконечно большая Þ неограниченная
Неограниченный: для " M > 0 $ n 0Î N: | xn | ³ M
Бесконечно большая: для "e>0 $ N 0: для всех n > N 0: | xn | > e
n = N 0+1 | xn | > e º M Þ $n
бесконечно большая Þ неограниченная. Обратное не верно:
| |
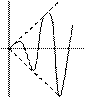
| xn = n *sin n неограниченная не бесконечно большая |
Последовательность называется фундаментальной, если для "e>0 $ N 0: " n > N 0 и "p=1,2,… | xn+p-xn |<e
Критерий Коши ( необ-е и дост-е усл-е ) Последовательность называется сходящейся тогда и только тогда, когда она является фундаментальной.
Функцией y = f (x) называется закон, по которому каждому значению x Î D (f)Ì R ставится в соответствие единственное действительное число y Î R. При этом множество значений аргумента D (f) называется областью определения функции, а множество значений { y | y = f (x), x Î D (f)}= E(f) называется множеством значений функции.
Функция может быть задана аналитически (то есть формулой), таблично или графически.
y = x 2
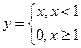
Если функция задана таблично, то чтобы найти значение функции для промежуточных значений аргумента применяют интерполяцию, заменяя функцию линейной, квадратичной на участке между двумя значениями аргумента.
Пусть точка x0 является предельной точкой области определения функции, тогда
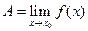 Û для "e > 0 $d > 0: " x Î D (f) Ç Ud(x 0) \ { x 0}: f (x) Î Ue(A)
Û для "e > 0 $d > 0: " x Î D (f) Ç Ud(x 0) \ { x 0}: f (x) Î Ue(A)
(Ue – e-окрестность).
Зачем \ { xn }. Например
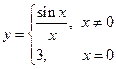
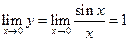 f (x 0=0) = 3 Ï Ue(1)
f (x 0=0) = 3 Ï Ue(1)
|
|
|
|
|
|
Дата добавления: 2015-01-03; Просмотров: 298; Нарушение авторских прав?; Мы поможем в написании вашей работы!