Реальная константа

Концентрационная константа

При расчетах равновесий в реальных системах необходимо учитывать присутствие посторонних веществ и их влияние на поведение исходных веществ и продуктов изучаемой реакции. Это влияние может выразиться и в электростатическом взаимодействии ионов, и в химическом взаимодействии с образованием малодиссоциированных или малорастворимых продуктов. В обоих случаях наблюдается сдвиг равновесия изучаемой реакции. Концентрационная константа выражается через общие концентрации, а не активности исходных веществ и продуктов реакции. В том случае, когда посторонние вещества не вступают в конкурирующие химические реакции, концентрационную константу можно выразить через равновесные концентрации. Для удобства изучения часто концентрационную константу, выраженную через равновесные концентрации, называют реальной константой, а концентрационную константу, выраженную через общие концентрации, – условной константой.

Состояние равновесия характеризуется реальной (концентрационной) константой

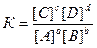
если отличия от идеальности обусловлены только электростатическими взаимодействиями А, В, С и D с посторонними ионами.

Активность и равновесная концентрация любого иона функционально связаны между собой простым соотношением. Например, для иона А

a_A = γ_A[A]

Коэффициент пропорциональности γ, называемый коэффициентом активности, характеризует степень отклонения системы от идеальной из-за электростатических взаимодействий ионов, участвующих в изучаемой реакции, с посторонними (или собственными, если их концентрация высока) ионами. В идеальной системе a_A = [А] и коэффициент активности равен единице. Это означает, что электростатические взаимодействия отсутствуют.

Величина коэффициента активности зависит от заряда и ионной силы, создаваемой всеми ионами в растворе:

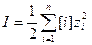(1-2)

Здесь I – ионная сила; [i] – равновесная концентрация иона; z_i — его заряд.

Коэффициенты активности индивидуальных ионов можно теоретически оценить по формулам Дебая - Хюккеля

если I < 0.01 (1-3)

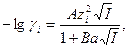если I < 0.1 (1-4)

Здесь А и В – константы, зависящие от температуры и диэлектрической проницаемости растворителя (для воды при 20°С А = 0.5 и B = 0.3); а – расстояние максимального сближения ионов; эти величины обычно приводятся в справочных таблицах. Поскольку колебания в значениях а не слишком сказываются на конечном результате, рекомендуется брать постоянное значение a = 3 А. Следовательно,

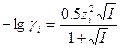(1-5)

Коэффициент активности индивидуального иона нельзя измерить экспериментально, так как нельзя получить раствор, содержащий только положительные или только отрицательные ионы.

Для электролита A_mB_n экспериментально можно определить лишь средний коэффициент активности, который связан с коэффициентами активности индивидуальных ионов γ_A и γ_B соотношениями:

для бинарного электролита АВ

для электролита типа A_mB_n

Средний коэффициент активности можно рассчитать и теоретически, используя формулы Дебая - Хюккеля

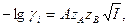если I < 0.01

если I < 0.1

Здесь а, А и В имеют те же значения, что и в формулах (1-3) и (1-4), поэтому

(1-6)

При низких ионных силах (I < 0.1) величины средних коэффициентов активности, рассчитанные по формулам Дебая - Хюккеля и найденные экспериментально, удовлетворительно совпадают. Это говорит о правомочности использования в этих условиях формул (1-3) - (1-4) для расчета величин γ_± и активности электролитов. Эти же формулы используются и для расчета коэффициентов активности индивидуальных ионов, хотя правильность таких расчетов нельзя проверить экспериментально.

Для более точного расчета коэффициентов активности предложено вводить в формулы Дебая - Хюккеля дополнительные члены. Например, уравнение Дэвиса позволяет вычислить коэффициенты активности электролитов и индивидуальных ионов для ионных сил 0.2 - 0.5 с погрешностью, не превышающей 10%. Уравнение Дэвиса для коэффициента активности индивидуального иона имеет вид:

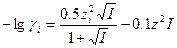(1-7)

а для среднего коэффициента активности электролита А_mВ_n:

Величины коэффициентов активности индивидуальных ионов при различных ионных силах и средние коэффициенты активности для растворов электролитов разной концентрации, рассчитанные по формулам Дебая - Хюккеля, приводятся в справочниках.

Зная коэффициенты активности, можно оценить активность иона или электролита в растворе. Для облегчения расчетов можно пользоваться следующими допущениями:

1. Коэффициенты активности ионов одинакового заряда независимо от радиуса ионов примерно равны. Поэтому в справочниках иногда приводятся усредненные величины коэффициентов активности для одно-, двух-, трех- и четырех-зарядных ионов.

2. Коэффициенты активности нейтральных частиц в разбавленных растворах электролитов полагают равными единице.

3. Очень разбавленные растворы электролитов, например насыщенный раствор малорастворимого электролита, можно считать идеальными.

ПРИМЕР 1. Рассчитайте активности ионов калия и сульфата в 0.10 М растворе сульфата калия.

Решение. Рассчитываем ионную силу, создаваемую ионами калия и сульфата

В справочнике находим, что при ионной силе 0.3

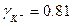и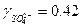

Поэтому в 0.10 М растворе сульфата калия

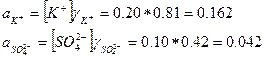
ПРИМЕР 2. Рассчитайте средний коэффициент активности для 0.10 М раствора гидроксида натрия и сравните его с экспериментально найденной величиной 0.764.

Решение. Рассчитываем ионную силу раствора:

По формуле Дебая - Хюккеля (1-6) находим γ_±:

, т.е. γ_± = 0,757

Как видно, в данном случае рассчитанное и экспериментально найденное значения среднего коэффициента активности близки; различие составляет 0.8%.

Часто при расчетах сложных равновесий коэффициенты активности принимают равными единице. Такое допущение оправдано по ряду причин. Во-первых, величины коэффициентов активности, найденные по формулам Дебая - Хюккеля, могут в этих случаях оказаться очень далекими от истинных. Во-вторых, влияние химических факторов на равновесие гораздо больше, чем электростатических сил, поэтому пренебрежение последними при расчетах сложных равновесий не вносит ощутимую погрешность в результаты.

Дата добавления: 2015-01-03