Степень образования комплекса и расчет равновесных концентраций

Если известны константы устойчивости комплексных соединений и равновесные концентрации свободного лиганда, можно рассчитать степень образования комплексного соединения в растворе (молярную долю):

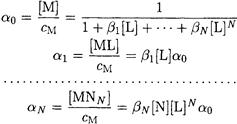
или в общем случае

(3-2)

ПРИМЕР 3. Какой комплекс преобладает в растворе, содержащем 1·10^{-2 М кадмия(II) и 1 М аммиака?}

Решение. В растворе, содержащем ионы кадмия и аммиак, устанавливаются следующие равновесия:

и далее но формуле (3-2)

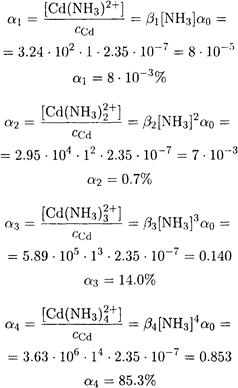
Расчет равновесных концентраций любых частиц в растворах комплексных соединений можно провести, используя уравнение материального баланса, а также функцию образования и степень образования. Часто ступенчатые константы устойчивости близки, и поэтому расчет равновесных концентраций бывает затруднительным. Для упрощения расчетов прибегают к ряду допущений:

1. При большом избытке лиганда можно полагать, что равновесная концентрация свободного лиганда равна его исходной концентрации.

2. При избытке металла можно полагать, что доминирующим является монолигандный комплекс.

3. В разбавленных растворах малоустойчивых комплексных соединений в отсутствие больших избытков лиганда маловероятно присоединение более чем одного-двух лигандов.

ПРИМЕР 4. Рассчитайте равновесную концентрацию Ag(NH₃)⁺ в 0.01 М растворе нитрата серебра, содержащем 2 М аммиака.

Решение. Запишем уравнение материального баланса для раствора, содержащего серебро (I) и аммиак:

По таблицам находим:

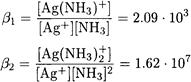
Выразив [Ag⁺] и [Ag(NH₃)⁺] через константы устойчивости β₁ и β₂, преобразуем уравнение материального баланса следующим образом:

Итак, неизвестна только концентрация Ag(NH₃)⁺:

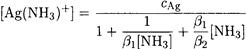
Поскольку C(NH₃) >> С(Ag), то можно считать, что [NH₃] = C(NH₃) = 2 M.

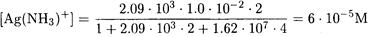
ПРИМЕР 5. Рассчитайте равновесные концентрации всех частиц в 0.010 М растворе хлорида кадмия (образованием гидроксокомплексов пренебречь).

Решение. В растворе хлорида кадмия существуют следующие равновесия:

Запишем уравнения материального баланса по кадмию и но хлорид-иону

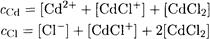
Поскольку имеем разбавленный раствор малоустойчивого комплексного соединения (β₁ = 112), образованием частиц, содержащих более одного лиганда, пренебрегаем. Это позволяет упростить уравнения материального баланса:

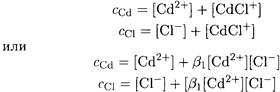
Из последнего уравнения найдем равновесную концентрацию иона кадмия:

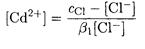
и подставим в уравнение материального баланса по кадмию

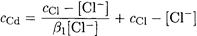
Рассчитываем равновесную концентрацию хлорид-иона:

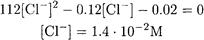
Теперь из уравнения материального баланса по хлорид-иону находим равновесную концентрацию иона кадмия:

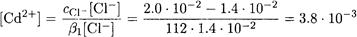
И, наконец, получаем значение равновесной концентрации CdCl⁺:

Эту задачу можно решать иначе. Если известны С_М и C_L, то для расчета равновесных концентраций всех частиц можно воспользоваться функцией образования (формула 3-1):

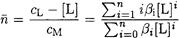
После преобразования получаем:

Пренебрегая существованием ионов CdCl₃^- и CdCl₄^2-, находим:

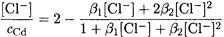
Отсюда

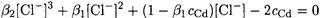
Поскольку первое слагаемое мало в сравнении с остальными, решаем квадратное уравнение

Зная [С1^-], несложно рассчитать равновесные концентрации остальных частиц.

ПРИМЕР 6. Рассчитайте равновесную концентрацию хлорид-иона в 0.01 М растворе нитрата кадмия в присутствии 0.01 М соляной кислоты.

Решение. Принимая во внимание, что С_Cd = С_Cl, а ступенчатые константы устойчивости CdCl⁺ и CdCl₂ заметно отличаются (112 и 3.55 соответственно), пренебрегаем существованием CdCl₂ полагая, что доминирующей формой в растворе является CdCl⁺.

Следовательно, упрощенные уравнения материального баланса можно записать так:

или после преобразования

Находим из последнего выражения равновесную концентрацию иона кадмия:

и подставляем в уравнение материального баланса по кадмию. Далее, сделав преобразования, как в предыдущем примере, получаем квадратное уравнение по равновесной концентрации хлорид-иона:

Подставив числовые значения и решив уравнение

ПРИМЕР 7. В 2 М растворе роданида калия содержится 1·10^{-1 М Fe(NCS)}₅^2-. Какую концентрацию фторид-иона необходимо создать, чтобы концентрация Fe(NCS)₅^2- понизилась до 1·10^{-5 М?}

Решение. Реакция Fe(NCS)₅^2- + 5F^- ↔ FeF₅^-2 + 5NCS^- характеризуется константой равновесия

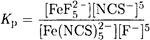
В справочных таблицах находим

Нетрудно видеть, что

Находим искомую величину [F^-]:

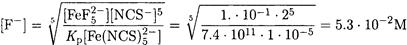
ПРИМЕР 8. Рассчитайте концентрацию несвязанного в комплекс кадмия (II) в растворе, полученном при сливании 50.0 мл 0.200 М раствора аммиака и 50.0 мл 0.0200 М раствора сульфата кадмия.

Решение. Общая концентрация аммиака значительно выше общей концентрации кадмия, поэтому уравнения материального баланса можно записать в упрощенном виде, полагая, что преобладает Cd(NH₃)₄²⁺.

Запишем уравнения материального баланса по кадмию ипо аммиаку

Далее,

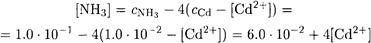
Подставляя найденные значения [NH₃] и [Cd(NH3)₄²⁺] в выражение для β4, получаем

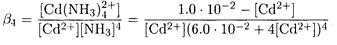
Упростим уравнение: поскольку концентрация аммиака довольно высокая, а комплекс устойчив, можно полагать, что концентрация несвязанного в комплекс кадмия мала. Поэтому

Рассмотрим другое возможное решение этой задачи. Поскольку C(NH₃) > С(Cd), то полагаем, что преобладает Cd(NH₃)₄²⁺ и его равновесная концентрация равна общей концентрации кадмия

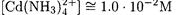
Для нахождения равновесной концентрации свободного аммиака воспользуемся выражением для среднего лигандного числа

Подставим найденные величины в выражение для β₄:

Дата добавления: 2015-01-03