Информационная логистика. Информационные потоки. Алгоритм Де Мукрона

Вопрос 32

В ней исследуются и разрабатываются информационные потоки (откуда поступают данные, откуда поступают результаты расчетов)

ИССЛЕДОВАНИЕ ИНФОРМАЦИОННЫХ ПОТОКОВ ПРОИСХОДИТ С ПОМОЩЬЮ РАЗЛИЧНЫХ МЕТОДОВ:

В.т.ч. графо-аналитическим методом матричного моделирования

Сущность метода – совокупность расчетов(задач, форм, документов) и их информативные связи представлены в виде напр. ориентированного графа, вершинами которого соотв. расчеты(з.п., себестоимости)сети логистического решения, а дуги связывают вершины графа, когда результаты одного расчета исп. Для дополнительной обработки.

В зависимости от цели исследования такой граф строят по отд. задачам (напр. по расчету себестоимости деталей), по комплексу задач.

Такой граф показывает взаимосвязи расчетов, циркулирующие в системе инф. потоки, но не отражает последовательность вып. расчетов.

Для определения очередности расчетов необходимо разбить вершины графа на слои так, чтобы все вершины данного слоя не имели предков в следующем слое.

Вершины первого слоя не имеют предков вообще, вершины посл. потомков.

Порядок вершин внутри одного слоя безразличен, т.е. они не соединены мужду собой дугами.

Матрица A=[auv] строится так:

· | auv | = 1, если между вершинами есть связь

· | auv | = 0, если связь отсутствует

n – число вершин графа

n\v

потомки1

предки1

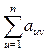
1 1

- показывает сколько раз n-ый показатель используется для расчета других показателей

если = 0, то n-ый показатель принадлежит к выходной информации.

По v-ому столбцу сумма от U=1, до n показывает сколько показателей используются при расчете данного v-го показателя, если она = 0, то V-ый показатель принадлежит к исходным данным.

Если для u=v åauv (сумма) = 0, то u-я вершина к рассматриваемому

графу не принадлежит, т.е. имеется ошибка при построении графа.= то u-я вершина к рассматриваемому графу медленно бежит, была допущена ошибка при построении графа.

Существует несколько методов разделения графа на слои

1. Возведение матрицы в степень Демукрона

Из суммы по столбцам,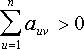

Вычитаются строки, соотв столбцам, в которых

1 слой:1,2,3

2 слой:4,5

3 слой:6,9,12

4 слой:8

5 слой:10,11

Сущ. требованием к алгоритму Демукрона является отсутствие замкнутых контуров, кроме ошибок. Основными причинами появления замкнутых контуров является наличие обратных связей между показателями.

Дата добавления: 2015-01-03