Решение задач 46—64 из учебника

Программа для Робика

Программы представляют собой последовательности (цепочки) команд. Программа должна выполняться последовательно, команда за командой, начиная с первой строки. Нельзя пропускать команды или выполнять их не подряд: это будет уже совсем другая программа. В задачах о Робике, как правило, заданы программа и начальная позиция и требуется дорисовать позицию после выполнения программы (выполнить программу). В таких задачах важно только понимание материала и внимательность при выполнении. Несколько большей трудностью отличаются задачи, в которых даны два поля: позиции до и после выполнения программы — и требуется восстановить пропуски в программе. При этом по внешнему виду клетки невозможно определить, побывал ли в ней Робик один раз или несколько.

На вкладыше в тетради проектов есть запасные поля для всех задач о Робике. Как их использовать, зависит от задачи и от ребёнка: это может быть черновик, с которого решение потом переносится в рабочую тетрадь, либо, если поле в рабочей тетради испорчено, можно его заклеить новым пустым полем и начать работать с начала.

Задачи 46 и 47. Это задачи на работу с новыми определениями. Важно выработать привычку правильно действовать при решении подобных задач. Обратите внимание на следующие моменты. Работа начинается с того, что раскраска клеток в начальной позиции переносится на поле Робика, которое должно стать позицией после выполнения программы (в рабочей тетради). Жирную точку пока не ставим, так как положение Робика собираемся менять. В начальной позиции в данных задачах закрашена только одна клетка, но, как следует из листа определения, возможна и более сложная предварительная раскраска. Переходим к работе с программой. Её необходимо выполнять шаг за шагом по следующей схеме: читаем команду, перемещаемся на одну клетку в заданном направлении, закрашиваем клетку, в которую попал Робик. При такой работе ошибки практически исключаются. Остаётся одна проблема — если ученик отвлечётся в процессе выполнения программы, то ему придётся начать работу заново, так как он потеряет последнюю выполненную команду. Чтобы исключить такую возможность, посоветуйте ребятам помечать в программе каждую команду после её выполнения. На каждом из полей в задачах 46 и 47 имеются стены. Но пока это не влияет на решение задачи (Робик сам обходит их при выполнении программы) — ребята просто привыкают к тому, что такое бывает.

Решение задач:

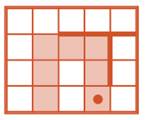
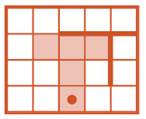
Задача 48. Программа в этой задаче не только длиннее, но и затейливее. Выше мы упоминали о том, что возможна потеря учащимся последней команды, и обсуждали, как этого избежать. Возможно и другое — потеря той клетки, где находится Робик после выполнения текущей команды. В таких задачах, как 46 и 47, где Робик не проходит дважды по одним клеткам и программа достаточно проста, такого обычно не происходит. Однако, если Робик движется с возвращениями, как в данной и во многих последующих задачах, это вполне вероятно. Необходимо иметь рецепт и на этот случай. Идея очевидна — отмечать текущее положение Робика, но вот как воплотить её в жизнь? Если на том же поле, на котором заштриховываем клетки, ещё помечать текущее положение, то может возникнуть неразбериха и грязь, ведь после каждого шага предыдущее текущее положение придётся стирать. Лучше делать это на другом поле, например на запасном поле из листа вырезания. Тогда алгоритм пошагового выполнения программы несколько усложнится и будет выглядеть так:

1) читаем очередную команду;

2) заштриховываем соответствующую клетку на поле, где должна быть позиция после выполнения программы;

3) помечаем точкой новое положение Робика на запасном поле, стирая при этом предыдущую пометку;

4) отмечаем выполненную команду в программе.

В данной задаче ещё можно без этого обойтись, но в дальнейшем проблема потери текущего положения будет вставать острее. Если вы увидите, что кто-то ошибается, то стоит уже сейчас обсудить, как избежать проблемы в дальнейшем.

Решение задачи:

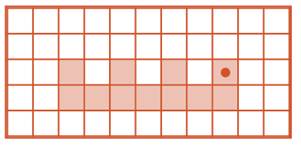
Задача 49. Задача на повторение лексики, относящейся к деревьям, в частности, понятий «уровень дерева», «следующий», «предыдущий», «корневая вершина», «лист дерева».

Решение задачи:

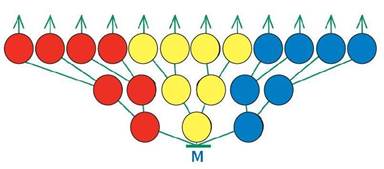
Задача 50. Задача, аналогичная задаче 48, только здесь имеются стены (которые пока никак не задействованы в задаче).

Решение задачи:

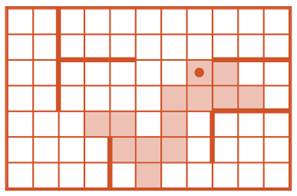
Задача 51 (необязательная). Задача, аналогичная задаче 26.

Задача 52. В начальной позиции на поле уже закрашено несколько клеток. Содержательного усложнения это пока не даёт, ребята должны лишь привыкнуть к тому, что такое бывает, и помнить, что, проходя по закрашенной клетке, Робик не меняет её цвет. Здесь особую актуальность приобретает подготовительный этап — аккуратное перенесение раскраски клеток начальной позиции на поле, где ребёнок будет выполнять программу.

Решение задачи:

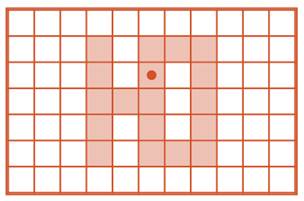
Задача 53. По условию известно, что в искомом дереве пять уровней и на каждом ровно один лист, значит, в дереве не меньше пяти вершин. Также понятно, что на каждом уровне, кроме последнего, должен быть хотя бы один не лист. Это ещё четыре вершины: итак, всего в дереве должно быть не меньше девяти вершин. При этом все цифры в вершинах должны быть разные, а разных цифр всего десять. Значит, вершин в дереве может быть девять или десять, причём на пятом уровне ровно одна, на четвёртом ровно две, а на остальных две или три. Конечно, такие рассуждения дети вряд ли проведут, но они придут к тем же самым выводам в ходе проб и ошибок. Поэтому попросите ребят строить дерево сначала карандашом и только после выполнения всех условий обводить ручкой.

Задача 54 (необязательная). Эта задача на повторение может занять много времени у медлительных детей, поэтому она предлагается в качестве необязательной. Таблица большая — 4 × 5 клеток, и есть вероятность, что кто-то посмотрит число не в той клетке или раскрасит не тот фрукт. Чтобы этого не случилось, посоветуйте ребятам выработать определённую систему раскрашивания. Например, можно раскрашивать фрукты по строчкам (или по столбцам) таблицы. Полезно сразу помечать ту клетку в таблице, которую уже использовали.

Задача 55. Это первое задание, где, имея позицию Робика после выполнения программы, требуется заполнить пропуски в самой программе. Основная идея, работающая при решении подобных задач, проста: нельзя писать такие команды, при выполнении которых Робик попадёт в незакрашенные клетки.

Ответ: пропущенные команды определяются однозначно: вниз, влево, вверх, вправо.

Задача 56. При решении задачи удобно воспользоваться черновиком. Первое утверждение: «В этом слове буква Е идёт раньше буквы О». Пишем на черновике букву Е, а потом букву О так, чтобы оставалось свободное место перед буквой Е, после буквы О и между буквами (ведь мы не знаем, куда придётся вставлять остальные буквы). Второе утверждение не связано с уже написанными буквами, поэтому пока займёмся третьим. Оказывается, буква У идёт позже О, значит, пишем на черновике букву У после буквы О (опять оставляя место между буквами). Возвращаемся ко второму утверждению и получаем следующую последовательность: Е — О — У — Ы. Остаётся вставить буквы в окна в соответствии с порядком их следования в слове. Кто-то из ребят впишет буквы мгновенно. Причина в том, что наша цепочка — осмысленное слово (БЕЛОКУРЫЙ), которое можно просто угадать по имеющимся буквам, вообще не читая утверждения. Это тоже неплохо, но таких ребят нужно попросить определить истинность всех утверждений в задаче, другими словами, доказать, что это угаданное решение нам подходит. Наша задача не отучить ребят догадываться (роль интуиции при решении задач трудно переоценить), а научить проверять правильность своей догадки или находить ошибку.

Задача 57. Зачем мы даём слова на иностранном языке, да ещё на французском, ведь ясно, что на данный момент ребята с иностранными языками если и знакомы, то лишь поверхностно? Ребёнок не знает, как произносить слова, а запомнить «бессмысленную», «беззвучную» последовательность букв трудно даже на короткое время, тем более что некоторые слова весьма длинны. Дело в том, что наша цель не изучение чужого языка (как на уроках иностранного языка в школе), а погружение в новую для ребят языковую среду (как бывает в жизни). Жизнь так или иначе погружает ребят в иные языковые среды: названия магазинов, наименование и состав продуктов и многое другое бывает написано на иностранном языке, и ребята с этим сталкиваются.

Все приведённые слова — названия французских городов*. Вот как они читаются в фонетической транскрипции, русской графике и принятом переводе на русский. (Обратите внимание на различие двух последних чтений.) Приподнятой буквой н обозначается носовое произношение предшествующей согласной. При очень сильном огрублении можно считать, что здесь произносится н.

Ещё одна причина появления такой задачи — наличие в иностранных словах большого числа дефисов. К русским словам типа «жили-были» или «Баба-яга» ребёнок привыкает с детства, а вот к подобным словам из других языков мы потихоньку начинаем его приучать.

В условии задачи говорится о том, что в цепочке должны находиться все слова из мешка, но про то, что в мешке лежат все слова из цепочки, не говорится ничего, таким образом, в цепочке могут находиться и «лишние» слова.

Задача 58. Решение задачи:

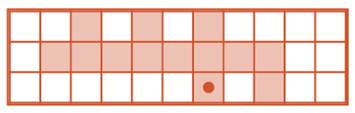
Задача 59 (необязательная). Задача на повторение словарного порядка слов. Сложность данной задачи в том, что в русском языке сравнительно мало слов на букву Ч. Сильно облегчат себе задачу ребята, которые будут помнить правило о расстановке в словарном порядке слов, одно из которых является частью другого. Например, слово ЧАЙ является частью слова ЧАЙКА, поэтому в словарном порядке идёт раньше него и позже слова ЧАДО, значит, подходит для заполнения первого окна. Для заполнения второго окна слово найти не так трудно, например: ЧАЙНИК, ЧАЙНЫЙ, ЧАЛМА, ЧАН, ЧАРКА. Заполнить третье окно оказывается сложней, поскольку таких слов не так уж много. Самый простой вариант — слово ЧАРОДЕЙ, которое является частью слова ЧАРОДЕЙКА, поэтому идёт в словарном порядке раньше.

Может случиться так, что кто-то из детей никак не может найти подходящее слово. Чтобы не подсказывать ему решение, можно просто дать ему в руки словарь. В этом случае, с одной стороны, вы не делаете всю работу за ребёнка, а с другой стороны — ребёнок тренируется в работе со словарём.

Задача 60 (необязательная). С подобным типом задания мы уже встречались в задаче 55. Будем использовать те же рассуждения. Выполним первые три команды программы У. Дальше команда пропущена, но мы видим, что, оставаясь в пределах раскрашенных после выполнения программы клеток, Робик может выполнить только одну команду — вниз, её и вписываем в окно. Выполняем следующие три команды. Ситуация стала немного иной — из этой клетки Робик может, оставаясь в пределах рисунка, выполнить команду как вверх, так и вниз. Но если Робик выполнит сейчас команду вверх, то не сможет затем выполнить следующую — вправо, значит, здесь подходит только команда вниз. Продолжаем выполнять известные команды программы, и остаётся последнее пустое окно. Его мы заполняем, исходя из положения Робика после выполнения программы. Это снова команда вниз.

Задача 61 (необязательная). Задача начинает новую серию задач, о которой стоит сказать несколько слов. Данные задачи находятся на стыке информатики и русского языка. При этом формальное информатическое (или математическое) решение, состоящее в полном переборе всех слов, имеющих такой мешок букв, детям осуществить будет довольно сложно. Так, если в слове пять разных букв (как в слове ВАЛИК), из них можно составить 120 разных цепочек букв. Поэтому, решая такие задачи, дети всё-таки больше угадывают слова, чем по-настоящему перебирают. Они интуитивно используют некоторые лингвистические соображения, например, какие сочетания букв более популярны в языке, а какие, наоборот, можно сразу отбрасывать. Поэтому вы, скорее всего, столкнётесь с тем, что кто-то из детей довольно легко будет решать такие задачи. Это те дети, у которых языковая интуиция развита хорошо. А у кого-то из ребят такие задачи не пойдут. При этом навести их на решение, не подсказав нужного слова, будет довольно затруднительно. Один из вариантов — предложить полный перебор, но подсказав первую букву искомого слова (тогда перебор существенно уменьшится). Для этого можно использовать дерево. В корневой вершине будет первая буква, в вершинах второго уровня — все возможные варианты второй буквы и т. д. Подобный способ решения такой задачи — это пропедевтика темы «Дерево вариантов», которой дети будут заниматься в 4 классе. Конечно, можно предложить подумать над задачей дома или оставить её на будущее. В любом случае такие задачи лучше предлагать по желанию, вполне допустимо, что ребёнок решит её частично (для каких-то слов).

Ответ: ВАЛИК — ВИЛКА (КИВАЛ)

УКЛОН — КЛОУН (КУЛОН, КОЛУН, ЛУКНО)

ЛОГИКА — ИГОЛКА

Задача 62 (необязательная). Дети, скорее всего, решали множество подобных задач, в которых точки пронумерованы или помечены русскими буквами. Здесь ситуация сложнее: наверняка не все ученики хорошо знают порядок букв в латинском алфавите, поэтому задача для них окажется непростой.

Можно провести дискуссию о частичном сходстве русской и латинской алфавитных цепочек: буква А идёт в русском алфавите раньше буквы Д, так же и в латинском алфавите буква A идёт раньше буквы D; буквы К, Л, М, Н, О, П, Р, С, Т, У в русском алфавите стоят в том же порядке, что и буквы K, L, M, N, O, P, R, S, T, U в латинском алфавите (впрочем, в латинском алфавите между буквами P и R есть ещё буква Q). Интересно было бы услышать от детей какое-нибудь разумное объяснение этого сходства (дело, конечно, в общем происхождении латинского и русского алфавитов от разных вариантов древнегреческого). Русские названия латинских букв дети найдут на второй странице обложки учебника.

Задача 63 (необязательная). Эта задача сложнее предыдущих задач о Робике. Робик мог начать выполнять программу из любой закрашенной клетки поля, включая ту, на которой он закончил свой путь. Поэтому если решать задачу «в лоб», то придётся проверять каждую программу из всех стартовых позиций. Для этого нужно будет перебрать 45 вариантов (девять программ из пяти возможных начальных позиций). Подумаем, как можно избежать такого громоздкого перебора.

Удобно выполнить все программы на листе бумаги в клетку (на «бесконечном» поле). Главное при этом — не забыть отметить положение Робика в конце выполнения программы (например, при выполнении четвёртой программы Робик закрашивает тот же рисунок, но в результате оказывается в другой клетке). В таком случае мы сразу поймём, какая программа подходит, ведь при её выполнении Робик закрасит тот же рисунок и остановится в том же месте рисунка, что и после выполнения программы С.

Однако выполнять все девять программ долго. Попробуем придумать идеи, которые ещё больше уменьшат перебор. Опыт, накопленный в предыдущих задачах про Робика, может подсказать ребятам, что в ту клетку, в которой Робик должен находиться после выполнения программы, он может попасть, только выполнив команду вправо. Таким образом, последняя команда программы должна быть вправо: вычёркиваем все программы, для которых это не верно. Остаются три подходящие программы, это существенно уменьшает перебор.

После того как правильная программа вырезана и наклеена, надо не забыть отметить положение Робика в начальной позиции.

Задача 64 (необязательная). Часто не только дети, но и взрослые не могут понятно объяснить дорогу из одного места в другое. Необходимый компонент такого умения — указание ясных, чётких и однозначных ориентиров, которые понятны всем. Один из способов указания ориентиров — лексика из темы «Цепочки». Это совершенно естественно, если речь идёт о домах, стоящих на одной стороне улицы, — они действительно образуют цепочку, нужно только указать направление движения.

Ответ:

Следующий дом после кинотеатра — это универсам.

Второй дом после универсама — это булочная.

Второй дом после кинотеатра — это аптека.

Кинотеатр называется «Сказка».

Следующий дом после универсама — это аптека.

Предыдущий дом перед аптекой — это универсам.

Предыдущий дом перед аптекой — это универсам.

Уроки «Перед каждой бусиной. После каждой бусины»

Мы живём в мире постоянно повторяющихся событий и явлений. Периодические цепочки играют в нашей жизни достаточно важную роль: смена времён года, месяцев, дней недели, дня и ночи, часы, идущие по кругу, — примеры периодических цепочек, в основе которых лежит конструкция «после каждой»: после каждого дня идёт ночь, после каждого вторника — среда, после каждого января — февраль и т. д. С периодическими цепочками мы пока работать не будем, а познакомим детей с понятиями «после каждой» и «перед каждой». Как и раньше, на этом листе определений мы рассматриваем ситуации, в которых утверждения становятся бессмысленными.

Дата добавления: 2015-01-03