Доверительный интервал для дисперсии при неизвестном среднем

Доверительный интервал для дисперсии при известном среднем

Здесь среднее 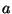считается известным фиксированным числом, а дисперсия 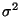выступает в роли неизвестного параметра. Положим

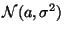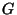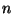Так как -- , то имеет стандартное нормальное распределение. Тем самым, функция имеет -распределение с степенями свободы, никаким образом не зависящее от неизвестного параметра 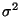. Обозначая через 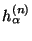квантили этого распределения и фиксируя некоторые , такие, что , приходим к неравенству

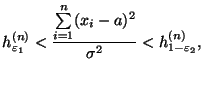
(47)

которое выполнено с вероятностью 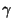. Откуда получаем 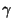-доверительный интервал для :

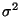Теперь оба параметра 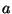и 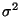будем считать неизвестными. Нас интересует доверительный интервал для 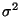. В этом смысле параметр 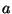является мешающим. Выберем

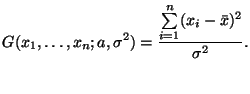
Заметим, что функция 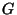определена таким образом, что при заданной выборке ее значения зависят лишь от параметра 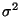. Что касается распределения случайной величины , то по теореме Фишера (см. 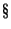8.3) оно является -распределением с степенями свободы и, следовательно, не зависит от неизвестных параметров. Фиксируя , такие, что , и рассуждая как в (47), приходим к следующему 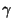-доверительному интервалу для :

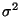который, используя обозначение (30), можно переписать так

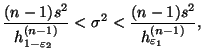
Дата добавления: 2014-12-23