Сложные группировки

Поточные линии для изготовления книг

Наиболее совершенной формой организации производства является поточный метод, который в настоящее время успешно применяется в брошюровочно-переплетных цехах для изготовления как книжной, так и брошюрной продукции. Для поточного метода организации производственного процесса необходимо:,

1. Все оборудование и рабочие места расположить последовательно по ходу технологического процесса.
2. Передачу полуфабрикатов по операциям технологического процесса необходимо производить безостановочно, для чего следует использовать различные транспортеры.
3. 
   Все оборудование на поточной линии должно работать с одинаковой скоростью, т. е. синхронно.

4. На каждой поточной линии рекомендуется выпускать опреде- енный тип продукции, например, только книги в твердом переплете или только брошюры, скомплектованные вкладкой.

5. Учитывая особенности поточного производства в брошюровочно- переплетном цехе, можно организовать поточные линии: по изготовлению книг в твердой переплетной крышке; по изготовлению брошюр, скомплектованных вкладкой; по изготовлению брошюр, скомплектованных подборкой.

1) к омбинационные – процедура выделения оптимального числа групп основана на применении формулы Стерджесса

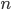§ — число групп

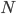§ — число единиц совокупности

Из формулы видно, что выбор числа групп зависит от объема совокупности. Если групп оказывается много и они включают малое число единиц, то групповые показатели могут стать ненадежными.

2) многомерные – осуществляется по комплексу признаков одновременно. Ее применение требует использования электронной вычислительной техники

Определение числа групп тесно связано с понятием величина интервала: чем больше число групп, тем меньше величина интервала, и наоборот.

Группировка - это распределение множества единиц исследуемой совокупности по группам в соответствии с существенным для данной группы признаком. Метод группировки позволяет обеспечивать первичное обобщение данных, представление их в более упорядоченном виде. Благодаря группировке можно соотнести сводные показатели по совокупности в целом со сводными показателями по группам. Появляется возможность сравнивать, анализировать причины различий между группами, изучать взаимосвязи между признаками. Группировка позволяет делать вывод о структуре совокупности и о роли отдельных групп этой совокупности. Именно группировка формирует основу для последующей сводки и анализа данных.

Если для построения группировки используется только один признак, то такую группировку называются простой, если группировка проводится по нескольким признакам, ее называют сложной. Сложная группировка бывает или комбинационная, или многомерная.

Комбинационная группировка выполняется последовательно: группы, выделенные по одному признаку, затем выделяются в подгруппы по другому признаку, которые, в свою очередь, могут выделяться по следующему другому признаку. В этом случае число групп будет равно произведению числа выделенных групп на число группировочных признаков. Процедура определения оптимального числа групп основана на применении формулы Стерджесса

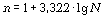
где n - число групп; N - число единиц совокупности.

Виды группировок зависят от целей и задач, которые они выполняют. С помощью метода статистических группировок выделяют качественно однородные совокупности, изучают структуры совокупности и изменения, происходящие в них, а также решают задачи по исследованию существующих связей и зависимостей.

С известной мерой условности для выполнения этих задач группировки соответственно делят на типологические, структурные и аналитические.

Метод типологической группировки заключается в выявлении в качественно разнородной совокупности однородных групп. При этом очень важно правильно отобрать группировочный признак, который поможет идентифицировать выбранный тип. Типологические группировки широко применяются в исследовании социально- экономических явлений.

Метод структурной группировки есть разделение однородной совокупности на группы по тому или иному варьирующему группировочному признаку. Примерами такого вида группировок могут быть группы населения по полу, возрасту, месту проживания, доходу и т.д.

Метод аналитической группировки заключается в исследовании взаимосвязей между факторными признаками в качественно однородной совокупности. С помощью аналитических группировок удается выявлять признаки, которые могут выступать или причиной, или следствием того или иного явления.

Относительные величины производны от деления текущего (сравниваемого) абсолютного показателя на базисный показатель.

Относительные показатели могут быть получены или как соотношения одноименных статистических показателей, или как соотношения разноименных статистических показателей. В первом случае получаемый относительный показатель рассчитывается или процентах, или в относительных единицах, или в промилле (в тысячных долях). Если соотносятся разноименные абсолютные показатели, то относительный показатель в большинстве случаев бывает именованным.

Относительные величины, используемые в статистической практике:

• относительная величина структуры;
• относительная величина координации;
• относительная величина планового задания;
• относительная величина выполнения плана;
• относительная величина динамики;
• относительная величина сравнения;
• относительная величина интенсивности.

Относительная величина структуры (ОВС) характеризует структуру совокупности, определяет долю (удельный вес) части в общем объеме совокупности. ОВС рассчитывают как отношение объема части совокупности к абсолютной величине всей совокупности, определяя тем самым удельный вес части в общем объеме совокупности (%):

(4.1)

где m_i - объем исследуемой части совокупности; M - общий объем исследуемой совокупности.

Относительная величина координации (ОВК) характеризует соотношение между двумя частями исследуемой совокупности, одна из которых выступает как база сравнения (%):

(4.2)

где m_i - одна из частей исследуемой совокупности; m_б - часть совокупности, которая является базой сравнения.

Относительная величина планового задания (ОВПЗ) используется для расчета в процентном отношении увеличения (уменьшения) величины показателя плана по сравнению с его базовым уровнем в предшествующем периоде, для чего используется формула

(4.3)

где Р_пл - плановый показатель; Р₀ - фактический (базовый) показатель в предшествующем периоде.

Относительная величина выполнения плана (ОВВП) характеризует степень выполнения планового задания за отчетный период (%) и рассчитывается по формуле

(4.4)

где Р_ф - величина выполнения плана за отчетный период; Р_пл - величина плана за отчетный период.

Относительная величина динамики (ОВД) характеризует изменение объема одного и того же явления во времени в зависимости от принятого базового уровня. ОВД рассчитывают как отношение уровня анализируемого явления или процесса в текущий момент времени к уровню этого явления или процесса за прошедший период времени. В результате мы получаем коэффициент роста, который выражается кратным отношением. При исчислении этой величины в процентах (результат умножается на 100) получаем темп роста.

Темпы роста можно просчитывать как с постоянным базовым уровнем (базисные темпы роста - ОВД_б), так и с переменным базовым уровнем (цепные темпы роста - ОВД_ц):

(4.5)

где Р_т - уровень текущий; Р_б - уровень базисный;

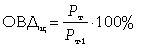(4.6)

где Р_т - уровень текущий; Р_т-1 - уровень, предшествующий текущему.

Относительная величина сравнения (ОВСр) - соотношение одноименных абсолютных показателей, относящихся к разным объектам, но к одному и тому же времени (например, соотносятся темпы роста населения в разных странах за один и тот же период времени):

(4.7)

где М_А - показатель первого одноименного исследуемого объекта; М_Б - показатель второго одноименного исследуемого объекта (база сравнения).

Все предыдущие показатели относительных величин характеризовали соотношения одноименных статистических объектов. Однако есть группа относительных величин, которые характеризуют соотношение разноименных, но связанных между собой статистических показателей. Эту группу называют группой относительных величин интенсивности (ОВИ), которые выражаются, как правило, именованными числами. В статистической практике относительные величины интенсивности применяются при исследовании степени объемности явления по отношению к объему среды, в которой происходит распространение этого явления. ОВИ здесь показывает, сколько единиц одной совокупности (числитель) приходится на одну, на десять, на сто единиц другой совокупности (знаменатель).

Примерами относительных величин интенсивности могут служить, скажем, показатели уровня технического развития производства, уровня благосостояния граждан, показатели обеспеченности населения средствами массовой информации, предметами культурно-бытового назначения и т.д. ОВИ рассчитывается по формуле

(4.8)

где А - распространение явления; В_А - среда распространения явления А.

При расчете относительных величин интенсивности может возникнуть проблема выбора адекватной явлению базы сравнения (среды распространения явления). Например, при определении показателя плотности населения нельзя брать в качестве базы сравнения общий размер территории того или иного государства, в этом случае базой сравнения может быть лишь территория в 1 км². Критерием правильности расчета является сопоставимость по разработанной методологии расчета сравниваемых показателей, применяющихся в статистической практике.

Среднее в статистике это обобщающий показатель, характер-щий типичность проявления признака для всей совокупности в конкретных условиях места и времени. Средняя величина - это обобщающие показатели, в которых находят выражение действия общих условий, закономерностей изучаемого явления. Особенности средней величины: 1,абстрактность; 2,характерна только для качественно однородной совокупности. 3,среднее выявлет закономерность, присущей данному явлению в тех усл-ях, к-му соответствует. Виды: 1.степенные величины Основной средней величиной является средняя степенная. Она имеет следующий вид: где`Х - средняя величина; X - меняющаяся величина признака варианты; n - число признаков или вариант; m - показатель степени средней. В зависимости от величины показателя степени средней она принимает следующие виды: а). Средняя арифметическая невзвешенная, где m = 1. Она имеет вид: 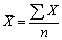б). Средняя арифметическая взвешенная. Она имеет вид: 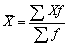где f - частоты или веса.

2.структурные величины Особый вид ср. вел-н структур. средние — применяется для изучения внутр строения рядов распр-я значений признака, а также для оценки ср вел-ны (степенного типа), если по имеющимся стат. данным ее расчет не м.б. выполнен. Для изучения структуры явления и выявления структур сдвигов прим. стукт. средней величины – это мода и медиана. Мода – это случ. величина вероятность появл. которой наибольшая ил это варианта частота повтор. наибольшая. Медиана – это серединная варианта в упоряд. ранжирование рядов.

Дата добавления: 2014-12-24