Нефинансовые активы 1 страница

27.

25.

23.

22.

20.

19.

18.

17.

16.

15.

13.

11.

10.

9.

Корреляционная связь - это связь, где воздействие отдельных факторов проявляется только как тенденция (в среднем) при массовом наблюдении фактических данных. Примерами корреляционной зависимости могут быть зависимости между размерами активов банка и суммой прибыли банка, ростом производительности труда и стажем работы сотрудников.

Наиболее простым вариантом корреляционной зависимости является парная корреляция, т.е. зависимость между двумя признаками (результативным и факторным или между двумя факторными). Математически эту зависимость можно выразить как зависимость результативного показателя у от факторного показателя х. Связи могут быть прямые и обратные. В первом случае с увеличением признака х увеличивается и признак у, при обратной связи с увеличением признака х уменьшается признак у.

Показатели тесноты связи между качественными признаками.

Для установления тесноты связи двух явлений, каждое из которых выражено только двумя альтернативными признаками, применяются коэффициенты ассоциации и контингенции. Они вычисляются с помощью табл. IV.5, показывающей числовые характеристики признаков.

К определению коэффициентов взаимной сопряженности

Явление Х и его словесные признаки	Явление Y и его словесные признаки	Итого
первый	второй
ПервыйВторой Итого:	а са + с	b db + d	a + bс + d a + b + с + d

Коэффициенты взаимосвязи явлений, показанных в таблице IV.5, определяются по формулам:

Коэффициент ассоциации: ;

Коэффициент контингенции: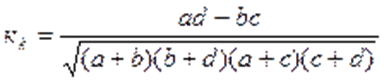

Для упрощения вычислений при значительных величинах a, b,c,d табл. IV.5 можно представить в структурном или долевом виде.

Явление Х и его словесные признаки	Явление Y и его словесные признаки	Итого
первый	второй
Первый Второй Итого:	d11 d21 d11 + d21	d12 d22 d12 + d22	d11 + d12 d21 + d221

Формула расчет коэффициента корреляции Пирсона следующая:

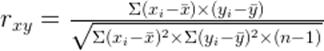
, где 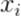— значения переменной X; 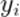— значения переменной Y; 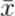— среднее арифметическое для переменной X; -среднее арифметическое для переменной Y.

Текущая формула коэффициент корреляции Пирсона предполагает, что мы должны взять разность между каждый значениям 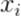переменной X, и ее средним значением 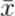. Однако в целях оптимизации расчетов для расчета коэффициента корреляции Пирсона используют получаемый с помощью преобразований аналог:

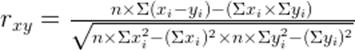
Статистическое наблюдение – это первая стадия всякого статистического исследования, представляющая собой научно организованный по единой программе учет фактов, характеризующих явления и процессы общественной жизни, и сбор полученных на основе этого учета массовых данных.
К статистическому наблюдению предъявляются следующие требования:
1) полноты и практической ценности статистических данных;
2) достоверности и точности данных;
3) их единообразия и сопоставимости.
Любое статистическое исследование необходимо начинать с точной формулировки его цели и конкретных задач, а тем самым и тех сведений, которые могут быть получены в процессе наблюдения. После этого определяются объект и единица наблюдения, разрабатывается программа, выбираются вид и способ наблюдения.
Объект наблюдения – совокупность социально-экономических явлений и процессов, которые подлежат исследованию, или точные границы, в пределах которых будут регистрироваться статистические сведения. Например, при переписи населения необходимо установить, какое именно население подлежит регистрации – наличное, т.е. фактически находящееся в данной местности в момент переписи, или постоянное, т.е. живущее в данной местности постоянно.
В ряде случаев для отграничения объекта наблюдения пользуются тем или иным цензом. Ценз есть ограничительный признак, которому должны удовлетворять все единицы изучаемой совокупности.
Единицей наблюдения называется составная часть объекта наблюдения, которая служит основой счета и обладает признаками, подлежащими регистрации при наблюдении.
Так, например, при переписи населения единицей наблюдения является каждый отдельный человек.
Программа наблюдения – это перечень вопросов, по которым собираются сведения, либо перечень признаков и показателей, подлежащих регистрации. Программа наблюдения оформляется в виде бланка (анкеты, формуляра), в который заносятся первичные сведения. Необходимым дополнением к бланку является инструкция (или указания на самих формулярах), разъясняющая смысл вопроса. Состав и содержание вопросов программы наблюдения зависят от задач исследования и от особенностей изучаемого общественного явления.Организационные вопросы статистического наблюдения включают в себя определение субъекта, места, времени, формы и способа наблюдения.
Отчетность – это такая организационная форма, при которой единицы наблюдения представляют сведения о своей деятельности в виде формуляров регламентированного образца.
С точки зрения полноты охвата фактов статистическое наблюдение может быть сплошным и несплошным. Сплошное наблюдение представляет собой полный учет всех единиц изучаемой совокупности. Несплошное наблюдение организуют как учет части единиц совокупности, на основе которой можно получить обобщающую характеристику всей совокупности.

Статистические показатели, расположенные в хронологическом порядке и отражающие изм-ия явления во времени называются рядом динамики. t- показатель времени (на дату, за период) y- уровень рада динамики. Классификация рядов динамики: 1. по временному показателю: а) если t – на дату – моментный ряд; Моментные ряды динамики отображают состояние изучаемых явлений на определенные даты (моменты) времени. Особенностью моментного ряда динамики является то, что в его уровни могут входить одни и те же единицы изучаемой совокупности. б) если t – за период – интервальный ряд. Интервальные ряды динамики отображают итоги развития (функционирования) изучаемых явлений за отдельные периоды (интервалы) времени.
Особенностью интервального ряда динамики является то, что каждый его уровень складывается из данных за более короткие интервалы времени.. 2. по выражению уровня ряда динамики: а) абсолютных показателей (количество выпущенной продукции по годам), б) относительных пок-лей (уровень рождаемости), в) средние величины (ср з/п,ср.душ. доход) 3 в зависимости от расстояния между уровнями: а) с равностоящими датами; б) с неравностоящими датами (увольнение, меняется численность). Показатели ряда динамики: К - темпы роста; цепной 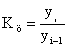, 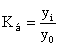. 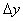- абсолютные приросты разность между двумя уровнями ряда динамики, имеет ту же размерность, что и уровни самого ряда динамики цепной абсолютный прирост - 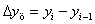; базисный абсолютный прирост - 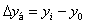. 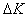- темпы прироста. относительный показатель, показывающий на сколько процентов один уровень ряда динамики больше (или меньше) другого, принимаемого за базу для сравнения. Базисные темпы прироста: 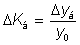. Цепные темпы прироста: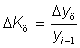

Динамический ряд — ряд однородных величин, характеризующих изменения явления во времени

Выделяют три основных способа обработки динамического ряда: а) укрупнение интервалов динамического ряда и расчет средних для каждого укрупненного интервала; б) метод скользящей средней.

Укрупнение интервалов - наиболее простой способ. Он заключается в преобразовании первоначальных рядов динамики в более крупные по продолжительности временных периодов, что позволяет более четко выявить действие основной тенденции (основных факторов) изменения уровней. По интервальным рядам итоги исчисляются путем простого суммирования уровней первоначальных рядов. Для других случаев расcчитывают средние величины укрупненных рядов (переменная средняя). Переменная средняя рассчитывается по формулам простой средней арифметической.

Скользящая средняя - это такая динамическая средняя, которая последовательно рассчитывается при передвижении на один интервал при заданной продолжительности периода. Сглаживание ряда динамики методом скользящей средней заключается в том, что вычисляется средний уровень из определенного числа первых по порядку уровней ряда, затем – средний уровень из такого же числа уровней начиная со второго, далее начиная с третьего и т.д. Каждое звено скользящей средней – это средний уровень за соответствующий период. При этом количество уровней, по которым рассчитывается скользящая средняя, называется шагом скольжения. Он выбирается в зависимости от длины динамического ряда и особенностей изучаемого явления.

Если, предположим, продолжительность периода равна 3 (месяца в квартале), то скользящие средние рассчитываются следующим образом:

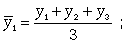Нанесите полученное среднее значение на график. На следующий месяц повторите операцию: сложите значения за предыдущие 3 месяца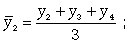

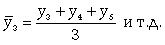
Более сложные методы и приемы расчета скользящей средней широко применяются, например, на рынке FOREX.

Важнейшим способом количественного выражения общей тенденции изменения уровней динамического ряда является

Аналитическое выравнивание — это более сложный прием выявления основных тенденций динамического ряда. Данный процесс включает два этапа:

1) выбор вида кривой (функции), форма которой соответствует характеру изменения динам-го ряда;

2) определение параметров и выравн-ых значений уровней динам-го ряда.

На первом этапе на линейном графике по фактическим данным строят ломаную кривую. При этом по оси абсцисс откладывают время, а по оси ординат — значения динамического ряда. Затем глазомерно оценивают ее и выбирают наиболее подходящую кривую. Это может быть прямая или парабола, показательная функция и т.д. Во всех случаях выбранная кривая должна удовлетворять методу наименьших квадратов. Его суть: 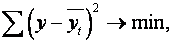где y — фактические уровни динамического ряда; 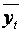— выровненные или теоретические уровни для каждого периода t.

На втором этапе аналитического выравнивания параметры функции, например прямой 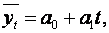определяются с помощью системы нормальных уравнений, например:

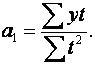
Определив 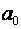и 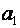, подставляют их значения в уравнение прямой, где t — время.

Трендовая модель считается адекватной описываемому процессу, если значения случайной остаточной компоненты ?t являются случайными центрированными некоррелированными нормально распределёнными величинами. Проверка адекватности модели состоит в проверке указанных свойств ряда остатков модели.

Проверка случайности остатков модели осуществляется с помощью критериев исследования временного ряда на предмет наличия в нём трендовой компоненты:

1) критерий, основанный на сравнении средних уровней временного ряда;

2) критерий «восходящих и нисходящих» серий;

3) критерий серий, основанный на медиане выборочной совокупности.

В этом случае вместо исходных уровней временного ряда y1,y2,…,yt используются элементы остаточного ряда e1,e2,…,et.

Также проверка случайности остатков модели может осуществляться с помощью критерия поворотных точек.

При использовании критерия поворотных точек остаток модели et сравнивается с двумя соседними элементами ряда. Если он окажется меньше или больше их, то данная точка является поворотной. В конце сравнений подсчитывается количество m всех поворотных точек. Ряд остатков модели считается случайным, если выполняется условие:

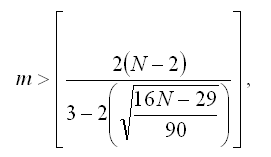
где N – объём выборочной совокупности.

Проверка центрированности остатков временного ряда осуществляется с помощью t-критерия Стьюдента.

Основная гипотеза формулируется как утверждение о центрированности ряда остатков.

Критическое значение t-критерия tкрит(?/2, N-1) определяется для уровня значимости ?/2 и числа степеней свободы (N-1) по таблице распределения Стьюдента.

Наблюдаемое значение t-критерия рассчитывается по формуле:

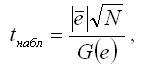
где

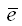
– среднее арифметическое значение ряда остатков:

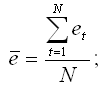
G(e) – среднеквадратическое отклонение ряда остатков:

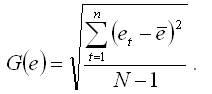
При проверке основной гипотезы возможны следующие ситуации.

Если наблюдаемое значение t-критерия (вычисленное по выборочным данным) больше критического значения t-критерия (определённого по таблице распределения Стьюдента), т. е. t набл ›t крит, то основная гипотеза отвергается. Следовательно, ряд остатков является не центрированным.

Если наблюдаемое значение t-критерия (вычисленное по выборочным данным) меньше или равно критического значения t-критерия (определённого по таблице распределения Стьюдента), т. е. tнабл?tкрит, то основная гипотеза принимается. Следовательно, ряд остатков является центрированным.

Проверка независимости ряда остатков модели осуществляется с целью определения возможной систематической составляющей в составе ряда остатков. Если модель подобрана неудачно, то остатки будут подвержены автокорреляционной зависимости.

Независимость остатков проверяется с помощью критерия Дарбина-Уотсона, связанного с гипотезой о наличии в ряде остатков автокорреляции первого порядка, т. е. о корреляционной зависимости соседних остатков.

Нормальность ряда остатков проверяется с помощью показателей асимметрии и эксцесса (если объём выборочной совокупности не превышает 50 значений). При нормальном распределении показатели асимметрии и эксцесса равны нулю.

На основании выборочных данных вычисляются эмпирические коэффициенты асимметрии и эксцесса по формулам:

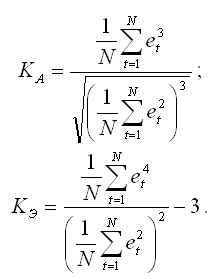
Если вычисленные коэффициенты близки к нулю, то можно сделать вывод, что ряд остатков подчиняется нормальному закону распределения.

В дополнение к выборочным коэффициентам асимметрии и эксцесса рассчитывают показатели среднеквадратических отклонений данных коэффициентов по формулам:

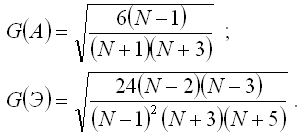
Если одновременно выполняются следующие неравенства:

1) |КА|?1,5G(A);

2) |КЭ|?1,5G(Э),

то гипотеза о нормальном характере распределения случайной компоненты принимается. Если хотя бы одно из указанных неравенств нарушается, то гипотеза о нормальном распределении остатков отвергается.

Помимо адекватности выбранной модели, необходимо охарактеризовать её точность. Наиболее простым критерием точности модели является относительная ошибка, рассчитываемая по формуле:

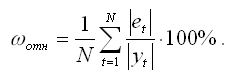
Если относительная ошибка равна менее, чем 13 %, то точность подобранной модели признаётся удовлетворительной.

14.

Сезонными называют колебания, связанные со сменой времен года или с регулярно повторяющимися из года в год событиями (праздники, посты, каникулы, выплата премий или дивидендов по итогам года и т.п.) и повторяющиеся, поэтому, ежегодно.

Виды сезонной составляющей временного ряда

детерминированная сезонная волна данный тип встречается в стабильно развивающихся экономиках

эволюционирующая сезонная волна данный тип характерен для экономики переходного периода

В экономике встречаются два вида сезонной составляющей динамического ряда, это:

1) детерминированная сезонная волна данный тип встречается в стабильно развивающихся экономиках (экономика США после «великой депрессии»)

2) эволюционирующая сезонная волна данный тип характерен для экономики переходного периода, т.к. в результате трансформации экономических механизмов, как правило, происходят изменения в механизме генерации динамического ряда (

Методы выделения сезонной составляющей в соответствии с типами сезонной волны можно также разделить на две группы.Для выявления детерминированной сезонной волны разработано большое количество алгоритмов, самыми распространенными из которых являются:

- исчисление индексов сезонности;

- десезонализация данных;

- сезонная декомпозиция временного ряда;

- фиктивные переменные;

- преобразование Фурье;В качестве алгоритмов выявления эволюционирующей сезонной волны можно назвать следующие методики:Процедура расчета индекса сезонности проста, на первом этапе данные выстраиваются в специальную таблицу

	2002г.	2003г.	2004г.		Индекс сезонности Iсез
1 квартал
2 квартал
3 квартал
4 квартал
Сумма	х	х	х

На следующем этапе рассчитывается средний уровень показателя по одноименным месяцам за ряд лет, для всех 12 месяцев (или 4 кварталов) тем самым исключается влияние случайных факторов. Далее рассчитывается средняя за год по усредненным по месяцам данным:На последнем этапе рассчитываются индексы сезонности по формулегде: t =1, 2, …, 12

Сущность и назначение индексного метода. Алгоритм расчета влияния факторов этим методом для разных моделей.

Индексный метод основан на относительных показателях динамики, пространственных сравнений, выполнения плана, выражающих отношение фактического уровня анализируемого показателя в отчетном периоде к его уровню в базисном периоде (или к плановому или по другому объекту).

С помощью агрегатных индексов можно выявить влияние различных факторов на изменение уровня результативных показателей в мультипликативных и кратных моделях.

Для примера возьмем индекс стоимости товарной продукции:

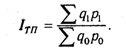
Он отражает изменение физического объема товарной продукции (q) и цен (р) и равен произведению этих индексов:

Чтобы установить, как изменилась стоимость товарной продукции за счет количества произведенной продукции и за счет цен, нужно рассчитать индекс физического объема Iq и индекс цен 1_p:

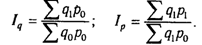
В нашем примере объем валовой продукции можно представить в виде произведения численности рабочих и их среднегодовой выработки. Следовательно, индекс валовой продукции 1вп будет равен произведению индекса численности рабочих lчр и индекса среднегодовой выработки 1гв:

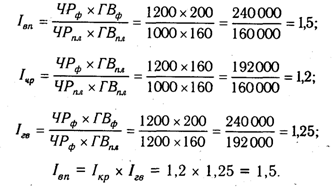
Если из числителя вышеприведенных формул вычесть знаменатель, то получим абсолютные приросты валовой продукции в целом и за счет каждого фактора в отдельности, т.е. те же результаты, что и способом цепной подстановки.

Индекс – это относительная величина, показывающая во сколько раз уровень изучаемого явления в данных условиях, отличается от уровня того же явления в других условиях.

Статистический индекс — это относительная величина сравнения сложных совокупностей и отдельных их единиц. При этом под сложной понимается такая статистическая совокупность, отдельные элементы которой непосредственно не подлежат суммированию.Основой индексного метода при определении изменений в производстве и обращении товаров является переход от натурально-вещественной формы выражения товарных масс к стоимостным (денежным) измерителям. Именно посредством денежного выражения стоимости отдельных товаров устраняется их несравнимость и достигается единство.

Виды индексов различают по следующим факторам:

§ по степени охвата элементов совокупности:

§ индивидуальные – характеризуют изменение только одного элемента совокупности;

§ сводные (общие) – отражают изменения по всей совокупности элементов сложного явления. Их разновидностью являются групповые индексы.

§ в зависимости от содержания и характера индексируемой величины:

§ индексы количественных показателей (например, индекс физического объема);

§ индексы качественных показателей (например, индекс цен, себестоимости, производительности труда).

§ в зависимости от методологии расчета:

§ агрегатные – могут быть рассчитаны как индексы переменного и постоянного состава;

§ средние из индивидуальных – получаются путем нахождения общих индексов с использованием индивидуальных.

§ Индекс физического объема продукции это индекс количественного показателя. В этом индексе индексируемой величиной будет количество продукции в натуральном выражении, а весом цена. Только умножив несоизмеримые между собой количества разнородной продукции на их цены, можно перейти к стоимостям продукции, которые будут уже величинами соизмеримыми. Так как индекс физического объема – индекс количественного показателя, то весами будут цены базисного периода. Тогда формула индекса примет следующий вид:

§

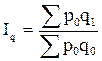
§ Индекс физического объема продукции показывает, во сколько раз возросла (уменьшилась) стоимость продукции из-за роста (снижения) объема ее производства или сколько % составляет рост (снижение) стоимости продукции в результате изменения физического объема ее производства.

§ К качественным показателям относят такие показатели, как цена, себестоимость, урожайность, производительность труда, заработная плата.

§ Индекс цен – это индекс качественного показателя. Индексируемой величиной будет цена товара, так как этот индекс характеризует изменение цен. Весом будет выступать количество произведенных товаров. Умножив цену товара на его количество, получаем величину, которую суммировать и которая представляет собой показатель, соизмеримый с другими подобными ему величинами.

§ Индекс цен определяется по следующей формуле:

§ .

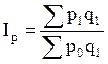§ Индекс показывает, во сколько раз возросла (уменьшилась) стоимость продукции из-за изменения цен, или сколько % составляет рост (снижение) стоимости продукции в результате изменения цен.

Для определения статистических индексов нужно иметь данные за два периода или два сравниваемых уровня.
Если существуют данные за определенный ряд периодов или уровней, то в качестве базы для сравнения можно принять один и тот же начальный уровень или уровень предыдущего периода. В первом случае получим индексы с постоянной базой – базисные, а во втором – индексы с переменной базой – цепные.
В экономическом анализе базисные и цепные индексы обладают определенными значениями.
Базисные экономические индексы характеризуют изменение статистических процессов за длительный период времени по отношению к одной отправной точке, но если возникнет необходимость следить за текущими изменениями статистического процесса, то применяются цепные индексы.
Если на основе базисных и цепных индексов исследуется один и тот же период, то это обозначает, что между ними есть взаимосвязь – это произведение цепных индексов, равное базисному. Такая взаимосвязь принесет возможность вычислить базисные индексы по данным цепных индексов, и наоборот.
Общие индексы характеризуют соотношение совокупности статистических процессов или явлений, состоящей из разнородных, непосредственно несоизмеримых элементов. Для определения общей стоимости различных видов продукции в качестве соизмерителя используется обычно цена за единицу продукции, для определения общей себестоимости или производственных затрат – себестоимость единицы продукции, общих затрат труда – затраты труда на производство единицы продукции и т. д.
Общее изменение товарооборота от стоимости проданных товаров можно определять, сопоставив общую стоимость проданных товаров в отчетном периоде по ценам отчетного периода с общей стоимостью проданных товаров в базисном периоде по ценам базисного периода.
Формула общего индекса товарооборота:

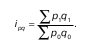
Аналогично индексу товарооборота рассчитываются индексы продукции, потребления и т. д.
Приведенная выше формула индекса товарооборота называется агрегатной (от лат. aggrega – «присоединяю»). Агрегатными называются индексы, числители и знаменатели которых представляют собой суммы, произведения или суммы произведений уровней изучаемого статистического явления. Агрегатная формула индекса – основная и наиболее распространенная формула экономических индексов. Агрегатная формула индекса показывает относительное изменение исследуемого экономического процесса и абсолютные размеры этого изменения.
Расчет агрегатного индекса цен был предложен немецким экономистом Г. Пааше.

Вариация — оценка индивидуальных значений признака по сравнению со средними.

Применение показателей вариации весьма разнообразно:
1) для оценки однородности совокупностей (совокупности);
2) для оценки концентрации и специализации производства;
3) для выявления аномальностей в совокупностях;
4) для сравнения вариации в различных совокупностях и их оценки.

Для характеристики колеблемости признака используется ряд показателей, такие как размах вариации, определяемый как разность между наибольшим (Х мах) и наименьшим (x mjn) значениями вариантов:

Дата добавления: 2014-12-24