Интервальные оценки комплексного показателя качества

Точечные оценки комплексного показателя качества

Тема 3.6. Виды оценок комплексного показателя качества.

Точечной называется оценка комплексного показателя качества Q, полученная по функции оценивания в виде одного числового значения. Для точечной оценки можно использовать формулы (3.26 – 3.29), а также (4.1) и (4.14) в зависимости от заданной погрешности оценивания и времени на оценивание.

Исследования показали, что расчеты по формуле (3.26) требуют малых затрат времени, но дают большую величину погрешности. Расчеты по формулам (4.1) или (4.14) более сложны математически, но обеспечивают вычисление Q с погрешностью ниже, чем по формуле (3.26), в 2-3 раза.

Точечные оценки (3.26 – 3.29, 4.1, 4.14) в значительной степени зависят от сочетаемых величин коэффициентов весомости q_i, составляющих в сумме 1,0. Любое перераспределение величин q_i приводит к изменению точечной оценки Q и в конечном итоге не позволяет с заданной достоверностью сравнивать полученные разными пользователями оценки. Это перераспределение объясняется прежде всего тем, что величины q_i задаются экспертными методами, отличающимися сложностью процедуры, трудоемкостью вычислений и слабой сопоставимостью результатов разных групп экспертов.

Недостатки точечной оценки комплексного показателя Q можно устранить его интервальной оценкой, под которой понимается интервал возможных значений в пределах Q_min…Q_max.

Суть предлагаемого интервального метода оценки Q можно представить так.

Поскольку выбор (назначение) коэффициента весомости q_i носит случайный характер (несколько реализаций q_ij, причем j = 1..m, где m – число экспертов), то и сам коэффициент весомости q_i является случайной величиной. Выборка q_ij, j = 1..m является малой (m < 20), следовательно, ее целесообразно анализировать методами малых выборок, среди которых наиболее широкое применение находят метод прямоугольных вкладов (МПВ) и метод уменьшения неопределенности (МУН). Целью данной статистической обработки является нахождение оценок математического ожидания и дисперсии случайной величины q_i, имея которые можно с помощью критерия Стьюдента найти нижние и верхние оценки q_i (q_{i min}, q_{i max}).

Плотность вероятности распределения по МПВ

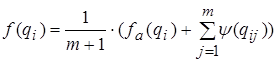, (3.30)

где 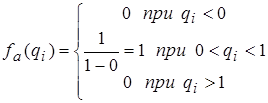(3.31)

- априорная функция плотности вероятности;

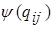- функция вклада – элементарное распределение, построенное относительно 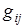- реализации и заданное на интервале ;

2 ·L = 1 – длина интервала, на котором строится функция вклада.

При использовании МУН вначале строят график накопленной вероятности и на его основе рассчитывают гистограмму (график плотности вероятности). По МУН

, (3.32)

где k_j – кратность q_ij – реализации весового коэффициента q _i.

При этом следует отметить, что МПВ более точен по сравнению с МУН, но более трудоемок.

Получив по МПВ или МУН или прочему методу гистограмму, можно рассчитать математическое ожидание и дисперсию весового коэффициента q_i:

. (3.33)

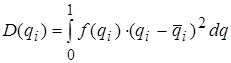. (3.34)

Далее можно записать нижние и верхние оценки границ интервала значений q_i при заданной доверительной вероятности P_d в виде

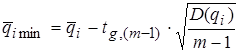, (3.35)

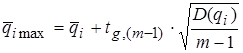, (3.36)

где g = 1 – P_d - вероятность ошибки;

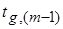- коэффициент Стьюдента.

Данный расчет повторяется для всех весовых коэффициентов q_i, i = 1, 2 …n. При этом все полученные значения весовых коэффициентов следует пронормировать:

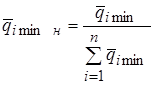, (3.37)

. (3.38)

Зная оценки весовых коэффициентов q_i, можно синтезировать оценки граничных значений комплексного критерия качества, например, по среднему арифметическому:

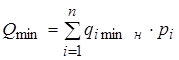; (3.39)

. (3.40)

Номинальное значение комплексного показателя качества

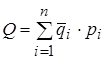, (3.41)

где 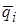- математическое ожидание соответствующего весового коэффициента. При расчете 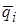следует их пронормировать.

Необходимо учитывать, что возможна ситуация Q_min > Q_max. Это является следствием операции нормирования весовых коэффициентов перед расчетом Q_min и Q_max. В таком случае за интервал значений следует принимать (Q_max, Q_min).

Предложенный метод повышает информативность единичных показателей качества p_i путем их идентификации по 2 дополнительным признакам – меньшие и большие.

Дата добавления: 2014-12-24