Тема 3.9. Расхождения в оценках комплексного показателя качества

Как было показано ранее, оценке качества Q можно сопоставить модель нормального распределения со следующими параметрами: математическим ожиданием и средним квадратическим отклонением

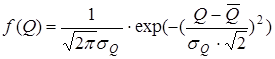. (3.50)

Если множество выбранных потребителем коэффициентов весомости не совпадает с множеством выставленных поставщиком, то это приведет к смещению интервальной оценки (3.6.2.) потребителя 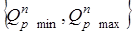относительно интервальной оценки изготовителя 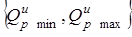, расхождению таких параметров, как средние значения (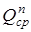, 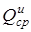) и средние квадратические отклонения (, ):

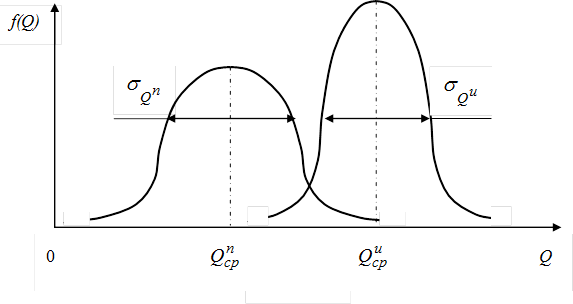
Задача состоит в том, чтобы расчетным путем установить, являются ли эти расхождения существенными (систематическими) или несущественными (случайными).

При этом различают сходимость и воспроизводимость количественных оценок качества Q.

Сходимость (повторяемость) оценок – это качество оценок, характеризуемое близостью друг к другу результатов расчета оценок, выполненных в одинаковых условиях.

Воспроизводимость оценок – это качество оценок, характеризуемое близостью друг к другу результатов расчета оценок, выполненных в различных условиях, разными методами и способами.

Наиболее типичным является контроль сходимости оценок, когда поставщик и потребитель для расчетов Q используют единую систему оценивания, а различия заключаются в значениях коэффициентов весомости.

Пусть для m экземпляров продукции получены оценки качества: .

Выборочное среднее арифметическое этих оценок качества

. (3.51)

Их выборочное среднее квадратическое отклонение

. (3.52)

Пусть задана нижняя допустимая граница качества Q_Н. Если любая оценка , или 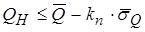, где k_п – критерий приемлемости (сходимости) оценок качества продукции, то сходимость оценок считается приемлемой (приемочной).

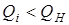Если или , то сходимость оценок качества продукции считается неприемлемой (браковочной).

Условие легко приводится к виду

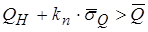. (3.53)

Тогда функция распределения величины

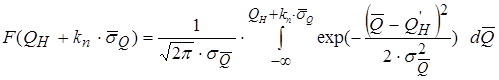, (3.54)

где расшифровано ниже.

Выражение (3.54) соответствует вероятности неприемлемости сходимости оценок.

Для последующих выводов воспользуемся известным положением

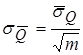. (3.55)

С учетом этого

. (3.56)

Приведем выражение (3.56) к нормализованному виду (3.57) подстановкой в (3.56) выражения (3.58):

. (3.57)

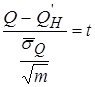. (3.58)

При приведенное значение уровня приемлемости t (t_кр) выразится как

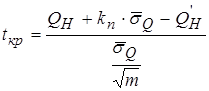. (3.59)

Вероятность приемлемости сходимости оценок

(3.60)

Зависимость (3.60) имеет два параметра: k_п и m. Их следует находить с учетом допустимых рисков поставщика α – отклонить приемлемую сходимость, и потребителя β – принять неприемлемую сходимость, а также приемочного q₀ и браковочного q_m значений вероятности возможного выхода оценок качества Q ниже границы Q_н.

Вероятность

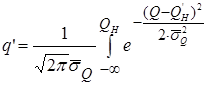. (3.61)

Далее используем подстановку

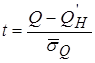, (3.62)

из которой следует, что

, (3.63)

где t_q – квантиль, соответствующий вероятности q.

После подстановки (3.61) преобразуется к виду

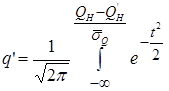. (3.64)

Таким образом, вероятности q’ соответствует квантиль

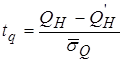, (3.65)

откуда

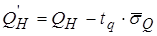. (3.66)

Подставляя (3.66) в (3.60), получаем зависимость вероятности приемлемой сходимости оценок качества продукции P_v(q’) от процента выхода q’ этих оценок за границу ниже Q_н:

. (3.67)

Учитывая (3.67), имеем:

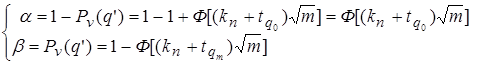. (3.68)

Эта система через квантили перепишется в виде

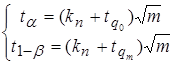, (3.69)

или, с учетом того, что , , ,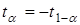

. (3.70)

Отсюда находим параметры плана контроля сходимости оценок качества продукции (k_п – критерий сходимости и m – объем выборки оценок)

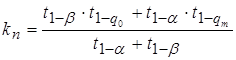. (3.71)

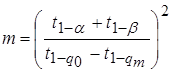. (3.72)

Последние выражения получены в предположении, что 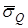- постоянная (неслучайная) величина. В действительности же 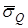является случайной величиной и имеет 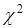- распределение. Этот факт имеет следствием то, что объем выборки следует вычислять с поправкой относительно (3.72):

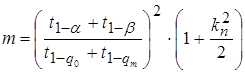. (3.73)

Дата добавления: 2014-12-24