Оценка параметров уравнения регреcсии. Пример

Задание:
По группе предприятий, выпускающих один и тот же вид продукции, рассматриваются функции издержек:
y = α + βx;
y = α x^β;
y = α β^x;
y = α + β / x;
где y – затраты на производство, тыс. д. е.
x – выпуск продукции, тыс. ед.

Требуется:
1. Построить уравнения парной регрессии y от x:

• линейное;
• степенное;
• показательное;
• равносторонней гиперболы.

2. Рассчитать линейный коэффициент парной корреляции икоэффициент детерминации. Сделать выводы.
3. Оценить статистическую значимость уравнения регрессии в целом.
4. Оценить статистическую значимость параметров регрессии и корреляции.
5. Выполнить прогноз затрат на производство при прогнозном выпуске продукции, составляющем 195 % от среднего уровня.
6. Оценить точность прогноза, рассчитать ошибку прогноза и его доверительный интервал.
7. Оценить модель через среднюю ошибку аппроксимации.

Посмотрите, как легко было найдено уравнение степенной регрессии с помощью сервиса.

Решение:

1. Уравнение имеет вид y = α + βx
1. Параметры уравнения регрессии.
Средние значения

Дисперсия

Среднеквадратическое отклонение

Коэффициент корреляции

Связь между признаком Y фактором X сильная и прямая
Уравнение регрессии

Коэффициент детерминации
R ²= 0.94 ² = 0.89
т.е. в 88.9774 % случаев изменения х приводят к изменению y. Другими словами - точность подбора уравнения регрессии - высокая

x	y	x ^2	y ^2	x ∙ y	y(x)	(y-y cp) ^2	(y-y(x))^2	(x-x p) ^2
					142.16	115.98	83.83
					148.61	17.9	0.37
					156.68	95.44	514.26
					143.77	104.67	104.67
					159.9	332.36	4.39
					187.33	2624.59	58.76
					124.41	22.75	212.95
					158.29	202.51	0.08
					134.09	67.75	320.84
					156.68	332.36	28.33
					138.93	231.98	402.86
					201.86	854.44	832.66
					16.3	20669.59	265.73
						25672.31	2829.74

Оценка параметров уравнения регрессии
По таблице Стьюдента находим Tтабл
Tтабл (n-m-1;a) = (11;0.05) = 1.796
Поскольку Tнабл > Tтабл, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициента корреляции статистически - значим.
Интервальная оценка для коэффициента корреляции (доверительный интервал)

Доверительный интервал для коэффициента корреляции
r(0.8884;0.9982)
Анализ точности определения оценок коэффициентов регрессии
S a = 0.1712
Доверительные интервалы для зависимой переменной
Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и X = 1
(-20.41;56.24)
Проверка гипотез относительно коэффициентов линейного уравнения регрессии
1) t-статистика
Статистическая значимость коэффициента регрессии a подтверждается
Статистическая значимость коэффициента регрессии b не подтверждается
Доверительный интервал для коэффициентов уравнения регрессии
Определим доверительные интервалы коэффициентов регрессии, которые с надежность 95% будут следующими:
(a - t a S a; a + t aS a)
(1.306;1.921)
(b - t b S b; b + t bS b)
(-9.2733;41.876)
2) F-статистики
Fkp = 4.84
Поскольку F > Fkp, то коэффициент детерминации статистически значим

36. Статистические характеристики тесноты связи: эмпирическое корреляционное отношение, линейный коэффициент корреляции, коэффициент детерминации.

Межгрупповая и общая дисперсии помогают определить, на сколько сильно результат педагогического эксперимента (или любого другого опыта) обусловлен принадлежностью испытуемого к той или иной группе. Для этого используетсякоэффициент детерминации .

Рассмотрим пример. Пусть оценки, полученные на ЕГЭ по математике выпускниками классов с разными профилями, описаны в следующей таблице.

Профиль класса (группа)	Средний балл в группе, xi	Численность группы (чел.), ni	Дисперсия в группе, Di
Общеобразовательный			10,15
Гуманитарный			9,81
Естественно-географический			12,3
Физико-математический			8,6

Определим, в какой степени успешность сдачи ЕГЭ зависит от принадлежности учащегося к той или иной группе. Для этого сначала найдем средний балл за экзамен для всей совокупности испытуемых:

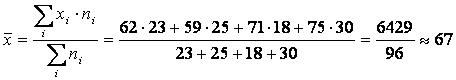
Найдем межгрупповую дисперсию:

Далее следует определить внутригрупповую дисперсию:

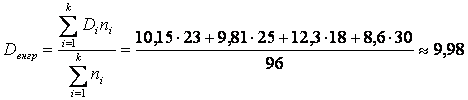
Определим общую дисперсию:Dв=Dвнгр+Dмежгр=9,98+45,66=55,64. Следовательно: .

Полученный коэффициент детерминации показывает, что успешность сдачи ЕГЭ в данном опыте на 82% обусловлена принадлежностью учащегося к той или иной группе.

Используют также эмпирическое корреляционное отношение, получаемое извлечением квадратного корня из коэффициента детерминации.

В рассмотренном примере . Чем ближе значение корреляционного соотношения к единице, тем более тесную связь мы наблюдаем. Соответственно, в данном случае было показано наличие тесной связи между успешностью сдачи ЕГЭ и принадлежностью учащегося к той или иной группе обучаемых.

Общая дисперсия помогает численно оценить, как сильно отличаются варианты выборки друг от друга. Межгрупповая дисперсия помогает выявить степень различия между группами данной выборки. Однако, в педагогических исследованиях зачастую не требуется численная оценка параметра, но при этом важно знать, существенно ли отличаются испытуемые (или группы испытуемых) друг от друга по тому или иному признаку. Ответ на такой вопрос даёт коэффициент вариации.

Расчет линейного коэффициента корреляции Пирсона:

Линейный коэффициент корреляции принимает значения от –1 до +1.
Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока:
0.1 < rxy < 0.3: слабая;
0.3 < rxy < 0.5: умеренная;
0.5 < rxy < 0.7: заметная;
0.7 < rxy < 0.9: высокая;
0.9 < rxy < 1: весьма высокая;

37. Методы изучения связи альтернативных признаков. Коэффициенты ассоциации, контингенции и взаимной сопряженности. Анализ и интерпретация.

В статистической практике могут встречаться такие случаи, когда качества факторных и результативных признаков не могут быть выражены численно. Поэтому для измерения тесноты зависимости необходимо использовать другие показатели. Для этих целей используются так называемые непараметрические методы.

Наибольшее распространение имеют ранговые коэффициенты корреляции, в основу которых положен принцип нумерации значений статистического ряда. При использовании коэффициентов корреляции рангов коррелируются не сами значения показателей х и у, а только номера их мест, которые они занимают в каждом ряду значений. В этом случае номер каждой отдельной единицы будет ее рангом.

Коэффициенты корреляции, основанные на использовании ранжированного метода, были предложены К. Спирмэном и М. Кендэлом.

Коэффициент корреляции рангов Спирмэна (р) основан на рассмотрении разности рангов значений результативного и факторного признаков и может быть рассчитан по формуле

(8.9)

где d = N_x - N_y, т.е. разность рангов каждой пары значений х и у; n - число наблюдений.

Ранговый коэффициент корреляции Кендэла () можно определить по формуле

(8.10)

где S = P + Q.

К непараметрическим методам исследования можно отнести коэффициент ассоциации К_ас и коэффициент контингенции К_кон, которые используются, если, например, необходимо исследовать тесноту зависимости между качественными признаками, каждый из которых представлен в виде альтернативных признаков.

Для определения этих коэффициентов создается расчетная таблица (таблица «четырех полей»), где статистическое сказуемое схематически представлено в следующем виде:

Признаки	А (да)	А (нет)	Итого
В (да)	a	b	a + b
В (нет)	с	d	c + d
Итого	a + c	b + d	n

Здесь а, b, c, d - частоты взаимного сочетания (комбинации) двух альтернативных признаков ; n - общая сумма частот.

Коэффициент ассоциации можно расcчитать по формуле

(8.11)

Коэффициент контингенции рассчитывается по формуле

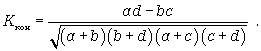(8.12)

Нужно иметь в виду, что для одних и тех же данных коэффициент контингенции (изменяется от -1 до +1) всегда меньше коэффициента ассоциации.

Если необходимо оценить тесноту связи между альтернативными признаками, которые могут принимать любое число вариантов значений, применяется коэффициент взаимной сопряженности Пирсона (К_П).

Для исследования такого рода связи первичную статистическую информацию располагают в форме таблицы:

Признаки	A	B	C	Итого
D	m11	m12	m13	∑m1j
E	m21	m22	m23	∑m2j
F	m31	m32	m33	∑m3j
Итого	∑mj1	∑mj2	∑mj3	П

Здесь m_ij - частоты взаимного сочетания двух атрибутивных признаков; П - число пар наблюдений.

Коэффициент взаимной сопряженности Пирсона определяется по формуле

(8.13)

где 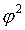- показатель средней квадратической сопряженности:

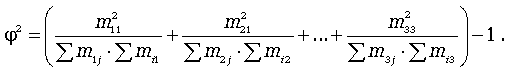
Коэффициент взаимной сопряженности изменяется от 0 до 1.

Наконец, следует упомянуть коэффициент Фехнера, характеризующий элементарную степень тесноты связи, который целесообразно использовать для установления факта наличия связи, когда существует небольшой объем исходной информации. Данный коэффициент определяется по формуле

(8.14)

где n_a - количество совпадений знаков отклонений индивидуальных величин от их средней арифметической; n_b- соответственно количество несовпадений.

Коэффициент Фехнера может изменяться в пределах -1,0 К_ф +1,0.

38.Изучение зависимости между количественными признаками. Ранговые показатели связи.

Для исследования взаимосвязи качественных альтернативных признаков, принимающих только 2 взаимоисключающих значения, используется коэффициент ассоциации и контингенции. При расчете этих коэффициентов составляется т.н. таблица 4-х камней, а сами коэффициенты рассчитываются по формуле:

Группы по признаку Y	Группы по признаку X	+	-	Итого:
+	a	b	a+b
-	c	d	c+d
Итого:	a+c	c+d	a+b+c+d

Если коэффициент ассоциации ³ 0,5, а коэффициент контингенции ³ 0,3, то можно сделать вывод о наличии существенной зависимости между изучаемыми признаками.

Если признаки имеют 3 или более градаций, то для изучения взаимосвязей используются коэффициенты Пирсена и Чупрова. Они рассчитываются по формулам:

С - коэффициент Пирсена

К - коэффициент Чупрова

j - показатель взаимной сопряженности

K - число значений (групп) первого признака

K1 - число значений (групп) второго признака

fij - частоты соответствующих клеток таблицы

mi - столбцы таблицы

- j - строки

Для расчета коэффициентов Пирсена и Чупрова составляется вспомогательная таблица:

Группа признака Y	Группа признака X			...	i	Итого:
	f11	f12	...	f1i	- 1
	f21	f22	...	f2i	- 2
...	...	...	...	...	...
j	fji	fj2	...	fji	- j
Итого:	m1	m2	...	mi	SSminj

При ранжировании качественных признаков с целью изучения их взаимосвязи используется коэффициент корреляции Кэндалла.

- - число наблюдений

S - сумма разностей между числом последовательностей и числом инвервий по второму признаку.

S=P+Q

P - сумма значений рангов, следующих за данными и превышающих его величину

Q - сумма значений рангов, следующих за данными и меньших его величины (учитывается со знаком «-»).

При наличии связанных рангов формула коэффициента Кендалла будет следующей:

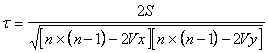
Vxи Vyопределяются отдельно для рангов Xи Yпо формуле:

39. Понятие и классификация рядов динамики

Рядами динамики называются последовательно расположенные в хронологическом порядке статистические данные, отображающие развитие изучаемого явления во времени.

В каждом ряду динамики имеются два основных элемента:

1. показатель времени t, который может быть представлен в виде определенных дат (моментов) времени, либо отдельных периодов (год, квартал, месяц, сутки);

2. уровни развития изучаемого явления у – отображают количественную оценку (меру) развития во времени изучаемого явления. Они могут выражаться абсолютными, относительными или средними величинами.

В зависимости от характера изучаемого явления уровни рядов динамики могут относиться или к определенным датам (моментам) времени, или к отдельным периодам. В соответствии с этим, ряды динамики подразделяются на:

1. моментные ряды динамики отображают состояние изучаемых явлений на определенные даты (моменты) времени, например, остатки товаров на складе готовой продукции на определенный момент времени (дату);

2. интервальные ряды динамики отображают итоги развития (функционирования) изучаемых явлений за отдельные периоды (интервалы) времени, например товарооборот предприятия за определенный период. Чем больше изменчивость явления во времени, тем меньше должны быть промежутки во времени между данными.

Отличительной особенностью моментного и интервального рядов динамики является понятие интервала. Для моментного ряда динамики интервал – промежуток времени между датами.
Кроме того, ряды динамики могут быть:

§ полный ряд - ряд динамики, в котором одноименные моменты времени или периоды времени строго следуют один за другим в календарном порядке или равноотстоят друг от друга.

§ неполный ряд динамики - ряд, в котором уровни зафиксированы в неравноотстоящие моменты или периоды времени.

40. Правила построения ряда динамики.

1. Периодизация развития, т.е. расчленение его во времени на однородные этапы, в пределах которых показатель подчиняется одному закону развития. По существу, это типологическая группировка во времени.

2. Статистические данные должны быть сопоставимы по территории, кругу охватываемых объектов, единицам измерения, времени регистрации, ценам, методологии расчета.

3. Величины временных интервалов должны соответствовать интенсивности изучаемых процессов. Чем больше вариация уровней во времени, тем чаще следует делать замеры, соответственно для стабильных процессов интервалы можно увеличить.

4. Числовые уровни рядов динамики должны быть упорядоченными во времени. Не допускается анализ рядов с пропусками отдельных уровней, если же такие пропуски неизбежны, то их восполняют условными расчетными значениями.

41. Показатели анализа ряда динамики

При изучении явления во времени перед исследователем встает проблема описания интенсивности изменения и расчета средних показателей динамики. Решается она путем построения соответствующих показателей. Для характеристики интенсивности изменения во времени такими показателями будут:
1) абсолютный прирост,
2) темпы роста,
3) темпы прироста,
4) абсолютное значение одного процента прироста.

Расчет показателей динамики представлен в следующей таблице.

Показатель	Базисный	Цепной
Абсолютный прирост 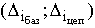^*	Yi-Y0	Yi-Yi-1
Коэффициент роста (Кр)	Yi : Y0	Yi: Yi-1
Темп роста (Тр)	(Yi : Y0)×100	(Yi : Yi-1)×100
Коэффициент прироста (Кпр)^**
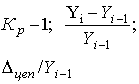
Темп прироста (Тпр)
Абсолютное значение одного процента прироста (А)

^*
**

В случае, когда сравнение проводится с периодом (моментом) времени, начальным в ряду динамики, получают базисные показатели. Если же сравнение производится с предыдущим периодом или моментом времени, то говорят о цепных показателях.

42. Структура ряда динамики. Проверка ряда на наличие тренда.

Всякий ряд динамики теоретически может быть представлен в виде составляющих:

Ø тренд – основная тенденция развития ряда, обусловливающая увеличение или снижение его уровней;

Ø циклические (периодические) колебания (в том числе сезонные);

Ø случайные колебания.

Проверка ряда динамики на наличие в нем тренда возможна несколькими способами (в порядке усложнения):

1. Графический метод, когда на графике по оси абсцисс откладывается время, а по оси ординат – уровни ряда. Соединив полученные точки линиями, в большинстве случаев можно выявить тренд визуально.

2. Метод средних, согласно которому изучаемый ряд динамики делится на два равных подряда, для каждого из которых определяется средняя величина и 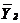. И если они различаются существенно (более 10%), то признается наличие тренда.

3. Метод Кокса и Стюарта, согласно которому ряд динамики делится на три равные по числу уровней группы и существенное различие выявляется между средними уровнями первой и третьей групп. Если общее число уровней не делится на три, то надо добавить недостающий уровень или исключить излишний.

4. Метод Валлиса и Мура, согласно которому наличие тренда признается в том случае, если ряд не содержит либо содержит в приемлемом количестве фазы, т.е. перемену знака при определении абсолютного изменения цепным способом.

5. Метод серий, согласно которому каждый уровень ряда считается принадлежащим к одному из двух типов, например типу А – меньше медианного или среднего значения или типу В – больше его. Затем в образовавшейся последовательности типов устанавливается число серий R. Они называются последовательностью уровней одинакового типа, которая граничит с уровнями другого типа. Если в ряду динамики общая тенденция к росту или снижению уровней отсутствует, то число серий является случайной величиной, распределенной приближенно по нормальному закону (при n>30) или по распределению Стьюдента (при n<30). Следовательно, если закономерности в изменениях уровней нет, то случайная величина R оказывается в доверительном интервале

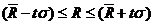
где t – коэффициент доверия для принятого уровня вероятности при нормальном законе или со степенью свободы k = (n - 1) при распределении Стьюдента;

– среднее число серий в ряду, определяемое по формуле: 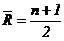; 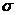– среднее квадратическое отклонение числа серий в ряду, определяемое по формуле .

Подставляя среднее число серий и его среднее квадратическое отклонение в доверительный интервал, получим его развернутое значение в виде

.

Значит, с заданной вероятностью тренд имеет место, если установленное число серий ряда не входит в доверительный интервал, и тренд отсутствует, если установленное число серий находится в этом интервале. 43. Анализ сезонных колебаний.

При анализе колеблемости динамических ря­дов наряду с выделением случайных колебаний, возникает за­дача изучения периодических колебаний. Как правило, изучение периодических (сезонных) колебаний необходимо с целью ис­ключения их влияния на общую динамику для выявления чи­стой (случайной) колеблемости.

К сезонным относят все явления, ко­торые обнаруживают в своем развитии отчетливо выраженную закономерность внутригодичных изменений, т.е. более или ме­нее устойчиво повторяющиеся из года в год колебания уровней. Часто эти колебания могут быть не связаны со сменой времен го­да. К сезонным явлениям относят, например, потребление элект­роэнергии; неравномерность производственной деятельности в отраслях пищевой промышленности, связанных с переработкой сельскохозяйственного сырья; перевозки пассажирским транспортом; спрос на многие виды продукции и услуги.

Как бы ни проявлялась сезонность, она наносит большой ущерб национальной экономике, связанной с неравномерным ис­пользованием оборудования и рабочей силы, с неравномерной за­грузкой транспорта, необходимостью создания резервов мощно­стей и т.д. Комплексное регулирование сезонных изменений по отдельным отраслям должно основываться на исследовании се­зонных отклонений.

Многие временные ряды имеют ярко выраженные сезонные компоненты, повторяющиеся с определенной периодичностью. Эта периодичность имеет место каждый год.

Если в анализируемой временной последовательности наблюдаются устойчивые отклонения от тенденции (в большую или в меньшую сторону), то можно предположить наличие в ряду динамики некоторых (одного или нескольких) колебательных процессов.

Это особенно заметно, когда изучаемые явления имеют сезонный характер, — возрастание или убывание уровней повторяется регулярно с интервалом в один год (например, производство молока и мяса по месяцам года, потребление топлива и электроэнергии для бытовых нужд, сезонная продажа товаров и т.д.).

Задачи, которые необходимо решить в ходе исследования сезонности:

1. выявить наличие сезонности;
2. численно выразить сезонные колебания;
3. выделить факторы, вызывающие сезонные колебания;
4. оценить последствия сезонных колебаний;
5. провести математическое моделирование сезонности.

Для измерения сезонных колебаний статистикой предложе­ны различные методы. Наиболее простые и часто употребляемые из них:

1. метод абсолютных разностей;
2. метод относительных разностей;
3. построение индексов сезонности.

Первые два способа предполагают нахождение разностей фак­тических уровней и уровней, найденных при выявлении основ­ной тенденции развития (тренда).

Применяя способ абсолютных разностей, оперируют непос­редственно размерами этих разностей, а при использовании ме­тода относительных разностей, определяют отношение абсолют­ных размеров указанных разностей к выровненному уровню. При выявлении основной тенденции используют либо метод сколь­зящей средней, либоаналитическое выравнивание. В некоторых случаях в стационарных рядах можно пользоваться разностью фактических уровней и средним месячным уровнем за год. Использование данных за несколько лет связано с тем обстоятельством, что в отклоне­ниях по отдельным годам сезонные колебания смешиваются со случайными. Чтобы элиминировать случайные колебания, берут средние отклонения за несколько лет.

Для выделения сезонной волны надо определить средний уровень за каждый месяц по 3-5-летним дан­ным и общую среднюю за весь рас­сматриваемый период.

Общая средняя получается делением суммы уровней за все три-пять лет на 36 или 60 (общее число месяцев). Затем определяется абсолютное отклонение средних месячных показателей от общей средней.

Метод абсолютных разностей заключается в расчете месячных средних и общей средней с последующим их сравнением:

• y_t — средний месячный уровень показателя за три и более лет,
• y_c — среднемесячное значение показателя за все годы.

Если сезонность оценивается по данным за 3 года (36 месяцев), если за 5 лет (60 месяцев):

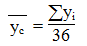
где: y_i — значение уровня динамического ряда. Величина и знак значений абсолютных отклонений определяют наличие сезонности.

В качестве показателя, характеризующего сезонную неравномерность, используется показатель относительного отклонения.

Метод относительных разностей является развитием метода абсолютных разностей. Для нахождения относительных разно­стей абсолютные отклонения делят на общую среднюю и выра­жают в процентах. По величине и знакам значений относительных отклонений можно судить о величине и силе влияния сезонного фактора.

Вместо относительных разностей за каждый месяц может быть вычислен индекс сезонности, который рассчитывается как отно­шение среднего уровня соответствующего месяца к общей сред­ней. Индекс сезонности рассчитывается:

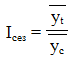
• y_t — средний уровень показателя соответствующего месяца за три и более лет,
• y_c — среднемесячное (по году) значение показателя за все годы (общая средняя).

Рассчитанные значения индекса сезонности сравниваются со значением 100 %. Если индекс сезонности превышает 100 % — это свидетельствует о влиянии сезонного фактора в сторону увеличения уровней динамического ряда и наоборот. Расчет индекса сезонности по данной формуле не учитывает наличие тренда. Выделение сезонной волны можно выполнить на основе по­строения аналитической модели проявления сезонных колебаний. Построение аналитической модели выявляет основной закон ко­леблемости данного временного ряда в связи с переходом от ме­сяца к месяцу и дает лишь среднюю характеристику внутригодичных колебаний.

44. Элементы прогнозирования и интерполяции.

Анализ динамики социально-экономических явлений, выявление и характеристика основной тенденции развития дают основание для прогнозирования - определения буду­щих размеров уровня экономического явления.

Процесс прогнозирования предполагает, что закономерность развития, действую­щая в прошлом (внутри ряда динамики), сохранится и в прогнозируемом будущем, то есть прогноз основан на экстраполяции. Экстраполяция, проводимая в будущее, называется перспективой, и в прошлое - ретроспективой. Обычно, говоря об экстраполяции рядов динамики, подразумевают чаще всего перспективную экстраполяцию. Первоначальные прогнозы, как правило, сводятся к экстраполяции тенденции. При этом могут использо­ваться разные методы, в зависимости от исходной информации. Можно выделить сле­дующие элементарные методы экстраполяции: на основе среднего абсолютного прироста, среднего темпа роста и экстраполяция на основе применения метода наименьших квадра­тов и представления развития явлений во времени в виде уравнения тренда, т.е. математи­ческой функции уровней ряда (у) от фактора времени (t).

Прогнозирование по среднему абсолютному приросту может быть выполнено в том случае, если есть уверенность считать общую тенденцию линейной, то есть метод ос­нован на предположении о равномерном изменении уровня (под равномерностью понима­ется стабильность абсолютных приростов).

В этом случае, чтобы получить прогноз на «i» шагов вперед (i - период упрежде­ния), достаточно воспользоваться следующей формулой:

(9.34.)

где у_n - фактическое значение в последней n-ой точке ряда (конечный уровень ряда);

- прогнозная оценка значения (п+1) уровня ряда; ∆¯ - значение среднего абсолютно­го прироста, рассчитанное для ряда динамики y_1; y_2; y_3;…; y_n.

Прогнозирование по среднему темпу роста можно осуществлять в случае, когда есть основание считать, что общая тенденция ряда характеризуется показательной (экспо­ненциальной) кривой. Для нахождения прогнозного значения на «i» шагов вперед необхо­димо использовать следующую формулу:

(9.35.)

где К¯_p - средний коэффициент роста, рассчитанный для ряда y_1; y_2; y_3;…; y_n.

К недостаткам рассмотренных методов следует отнести то, что они учитывают лишь конечный и начальный уровень ряда, исключая влияние промежуточных уровней. Тем не менее, методы среднего абсолютного прироста и среднего темпа роста имеют весьма широкую область применения, что объясняется простотой их вычисления. Они мо­гут быть использованы как приближенные, простейшие способы прогнозирования, пред­шествующие более глубокому количественно-качественному анализу.

Наиболее распространенным методом прогнозирования является аналитическое выражение тренда. При этом для выхода за границы исследуемого периода достаточно продолжить значения независимой переменной времени (t).

При таком подходе к прогнозированию предполагается, что размер уровня, харак-теризирующего явление, формируется под воздействием множества факторов, причем не представляется возможным выделить отдельно их влияние. В связи с этим ход развития связывается не с какими-либо конкретными факторами, а с течением времени. На практи­ке для описания тенденции развития явления широко используются модели кривых роста, представляющие собой различные функции времени у = f(t).

Процедура разработки прогноза с использованием кривых роста включает в себя следующие этапы: 1) выбор одной или нескольких кривых, форма которых соответствует характеру изменения ряда динамики; 2) оценка параметров выбранных кривых;-3) провер­ка адекватности выбранных кривых прогнозируемому процессу и окончательный выбор кривой роста; 4) расчет точечного и интервального прогнозов.

Остановимся на величине доверительного интервала прогноза, который определя­ется по формуле:

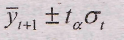9.36)

где:

σ - средняя квадратическая ошибка тренда;

y¯_t+1 - расчетное значение уровня;

t_a - доверительная величина, определяемая на основе t-критерия Стьюдента.

Вместо t_a - критерия удобно использовать коэффициент (К*).

Например, необходимо провести прогноз на 2005-2006 гг. по данным таблицы (9.5) количества проданных квартир в N-ом регионе.

Для экстраполяции используем уравнение тренда, полученное по прямой: y¯_t = 39,7 + 0,25t. Подставив соответствующее значение t в наше уравнение, получим то­чечные прогнозы на 2005-2006 гг. (графа 2 таблицы 9.9). Для построения интервальных прогнозов рассчитаем среднеквадратическую ошибку тренда (σ_t=0,56) и используем зна­чения К

Результаты прогноза представлены в таблице 9.9.

^ Таблица 9.9.
Прогнозные значения численности проданных квартир в N-ом регионе

Дата добавления: 2014-12-24