Уравнение движения механической системы привода при жестких кинематических связях

При жестких кинематических связях в МС привода можно считать, что эквивалентная МС представлена вращающейся массой, закрепленной на валу двигателя и имеющей момент инерции, равный сумме момента инерции ротора двигателя и приведенного момента инерции механизма:

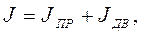
В МС привода действуют момент двигателя и момент сопротивления. В установившемся режиме М=М_С. При нарушении этого равенства возникает переходный режим работы привода. Разность М – М_С = М_ДИН называют динамическим моментом. Динамический момент обеспечивает приращение скорости привода. Если М › М_С, динамический момент положительный и приращение скорости так же положительно (привод ускоряется). Если динамический момент отрицателен, то приращение скорости привода так же отрицательно и привод замедляется. Таким образом, уравнение движения привода М = М_С + М_ДИН. В общем случае моменты двигателя и сопротивления могут быть нелинейными функциями скорости. При J = const уравнение движения привода имеет вид:

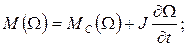(1)

Решение этого нелинейного дифференциального уравнения (при заданных начальных условиях) позволяет определить закон движения привода Ω(t). В случае переменного момента инерции J = J(φ) получается более сложное уравнение. Кинетическая энергия МС привода

Динамический момент на основе уравнения Лагранжа второго рода

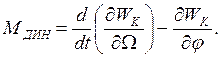
После дифференцирования получим:

(2)

Уравнения (1) и (2) дают полное описание МС привода при жестких кинематических связях. В частном случае при из уравнения (1) получается нелинейное алгебраическое уравнение статического режима:

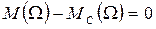
Решение этого уравнения, т.е. значение скорости Ω на которой работает привод в установившемся режиме находят как точку пересечения механических характеристик. Эту задачу решают численно или графически.

На рисунке МХ асинхронного электродвигателя работающего при постоянной М_С(Ω) и с вентиляторной нагрузкой. В точке 1 – устойчивая работа привода, т.к. β < 0. в точке 2 для М_С= const привод не устойчив (β > 0) и устойчив при вентиляторной нагрузке.

Дата добавления: 2014-12-24