Механические переходные процессы в электроприводах

В простейших электромеханических системах привода пренебрегают электрическими переходными процессами, т.к. изменения тока в цепях ЭД происходит быстрее изменения скорости. Решение уравнения движения привода можно значительно упростить если предположить, что момент сопротивление от скорости не зависит, а механическая характеристика привода линейна. В этом случае динамический момент М_ДИН(Ω) представляет собой линейную функцию скорости. Для привода с линейной механической характеристикой

.

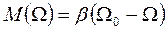Подставляя это выражение в уравнение движения привода (1) получим и

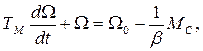(3)

где

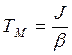- электромеханическая постоянная времени.

Это выражение: линейное неоднородное дифференциальное уравнение первого порядка.

Уравнение (3) содержат только механические параметры и представляет собой механическую модель электромеханического привода. Электрические параметры в такой модели явно не присутствуют. При установившемся режиме и угловая скорость установившегося режима Ω=Ω_У. Для установившегося режима из (3) получим

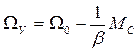
и

(4)

Решение (4) при начальных условиях Ω(0) = Ω_нач имеет вид

(5)

Если начальная угловая скорость равна нулю, то

Графики изменения скорости в переходном процессе при разгоне привода от начальной скорости до установившегося значения(кривая 1) представлен на рисунке. Формула (5) позволяет определить изменение скорости привода при изменении момента сопротивления. При этом произойдет изменение установившейся скорости от

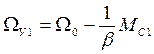
До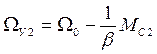

Если М_С2 > М_С1, то Ω_У2 < Ω_У1 в результате

Кривая (2) показывает как изменяется скорость при увеличении нагрузки. Электромеханическая постоянная времени Т_М определяет темп механических переходных процессов в приводе. При t=T_м скорость привода Ω = 0.632Ω_УСТ. Это соотношение часто принимают за определение электромеханической постоянной времени. Если провести касательную к графику Ω(t) в точке Ω(0) до пересечения с уровнем установившейся скорости, то абсцисса точки пересечения будет равна электромеханической постоянной времени. Отсюда вытекает другое определение T_м , как времени разгона электропривода до установившейся скорости при постоянном ускорении, равном начальному. Время переходного процесса определяется из уравнения движения привода

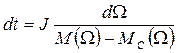
Время переходного процесса, необходимое для изменения скорости привода от Ω = Ω₁ до Ω = Ω₂

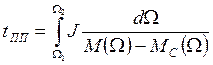
Для вычисления этого интеграла, надо знать зависимость движущего момента и момента сопротивления от скорости. В простейшем случае можно принять момент инерции величиной постоянной:

J = const, M = const, M_C = const,

Тогда:

По этой формуле можно определить время пуска привода под действием постоянного момента при постоянном моменте сопротивления. При этом Ω₁ = 0 Ω₂ = Ω_НОМ

Отсюда:

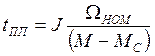
При торможении привода момент движения меняет знак и время торможения

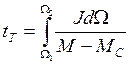
При постоянстве моментов и момента инерции

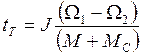
Время торможения от номинальной скорости Ω₁ = Ω_НОМ до скорости Ω = 0,

Время переходного процесса электропривода, имеющего линейную МХ при постоянном моменте сопротивления можно определить из уравнения изменения скорости. Для этого положим в (5) Ω_НАЧ = Ω₁ и Ω = Ω₂ и решим это уравнение относительно времени переходного процесса:

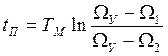
При Ω_У = Ω₂ этой формулой пользоваться нельзя. В этом случае приближенно принимают t_П = (3…4)Т_М.

Механическая характеристика асинхронного двигателя существенно не линейна поэтому достаточно простое выражение для времени переходного процесса t_ПП можно получить только для случая, когда М_С = 0. Приближенное время для пуска двигателя

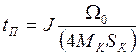
Для случаев, когда М_С ≠ 0 применяют приближенные методы решения уравнения электропривода.

Дата добавления: 2014-12-24