Лекция 7. Системы линейных уравнений. Арифметическое n-мерное векторное пространство. Метод Гаусса. Правило Крамера

Пусть дана система из 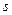линейных уравнений с 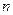неизвестными:

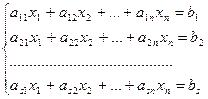(1)

Решением системы (1) называется упорядоченная система из 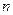чисел, удовлетворяющих этой системе. Эти числа при подстановке на место соответствующих переменных обращают вес уравнения системы в числовые равенства.

Определение. Упорядоченная система из 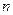действительных чисел называется 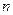-мерным арифметическим вектором. Суммой двух векторов называется вектор, компоненты которого есть суммы соответствующих компонент слагаемых векторов, произведением вектора а на число k называется вектор, компоненты которого равны произведению на k соответственных компонент вектора а. Совокупность всех 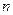-мерных векторов с действительными компонентами, рассматриваемая с определенными в ней операциями сложения векторов и умножения вектора на число, называется Е арифметическим п -мерным векторным пространством.

Если система (1) имеет хотя бы одно решение, то она называется совместной. Если не имеет ни одного решения, то она называется несовместной.

Совместная система называется определенной, если система имеет одно решение.

Если совместная система имеет больше одного решения, то она называется неопределенной.

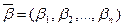Два решения и различны, если 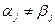. Однородная система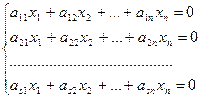

Эта система всегда совместна, т.к. .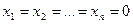

Задача теории систем линейных уравнений состоит в разработке методов, позволяющих узнать, совместна ли данная система уравнений или нет, в случае совместности установить число решений, а также указать способ найти все эти решения.

При определенных условиях решить систему можно с помощью правила Крамера.

Теорема. Пусть дана система .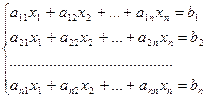

Если , то система имеет одно единственное решение, определяемое следующими формулами (формулами Крамера):

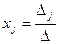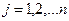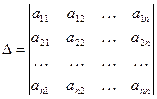, где , a 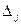получается из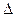

заменой 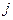- го столбца столбцом свободных членов.

Например,

;

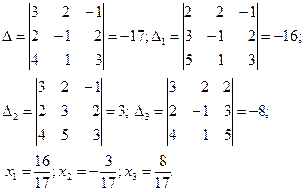
Отметим, что если определитель матрицы А коэффициентов квадратной системы линейных уравнений равен нулю, то возможен один из двух случаев: либо система несовместна, либо она совместна и неопределенна.

Пусть даны системы 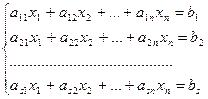(1) и

(2)

Определение. Две системы (1) и (2) с одинаковым количеством переменных называются эквивалентными (равносильными), если обе системы несовместны или обе совместны и обладают одними и теми же решениями.

Элементарные преобразования систем:

1) Перемена мест двух уравнений в системе;

2) Умножение обеих частей уравнения на число, отличное от 0;

3) Прибавление к частям какого-нибудь уравнения соответствующих частей другого уравнения, предварительно умноженных на какое-нибудь число;

4) Выбрасывание уравнения вида 0=0;

5) Перемена мест двух слагаемых во всех уравнениях системы.

Теорема. При элементарных преобразованиях система приводится к эквивалентной системе.

Определение. Система называется ступенчатой, если каждое уравнение имеет хотя бы 1 отличный от 0 коэффициент или свободный член и, начиная со 2-го уравнения, 1-ое отличное от 0 слагаемое расположено правее 1-го отличного от 0 слагаемого предыдущего уравнения

Теорема. Всякая система линейных уравнений при помощи элементарных преобразований приводится к равносильной ступенчатой системе.

Определение. Матрица 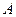называется ступенчатой, если любая её строка имеет хотя бы один неравный нулю элемент и если первый неравный нулю элемент её каждой строки, начиная со второй, расположены правее первого неравного нулю элемента предыдущей строки. В частности, квадратная ступенчатая матрица называется треугольной.

Определение. Элементарными преобразованиями матрицы называются следующие преобразования строк (столбцов):

1) перестановка двух каких-нибудь строк (столбцов);

2) умножение элементов какой-нибудь строки (столбца) матрицы на число ;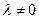

3) прибавление к элементам какой-нибудь строки (столбца) матрицы соответствующих элементов другой строки (столбца) той же матрицы, умноженных на некоторое число.

Теорема. Всякую ненулевую матрицу можно привести к ступенчатому виду с помощью элементарных преобразований и выбрасывания нулевых строк (столбцов).

Рассмотрим прямоугольную матрицу A, у которой число столбцов m больше, чем число строк n. Если матрицу A можно разделить вертикальной чертой на две матрицы: стоящую слева треугольную матрицу размера m и стоящую справа прямоугольную матрицу, то матрицу A назовем трапециевидной или трапецеидальной. Очевидно, что матрица (6) — трапециевидная матрица.

Если при применении эквивалентных преобразований к системе уравнений хотя бы одно уравнение приводится к виду

0 x ₁ + 0 x ₂ + ¼0 x_n = b_j (b_j ¹ 0),

то система несовместна или противоречива, так как ни один набор чисел x ₁, x ₂, ¼, x_n не удовлетворяет этому уравнению.

Если при преобразовании расширенной матрицы системы матрица коэффициентов приводится к трапецеидальному виду и при этом система не получается противоречивой, то система совместна и является неопределенной, то есть имеет бесконечно много решений.

В последней системе можно получить все решения, придавая конкретные числовые значения параметрам r и s.

Те переменные, коэффициенты при которых стоят на главной диагонали трапецеидальной матрицы (это значит, что эти коэффициенты отличны от нуля), называются базисными. В рассмотренном выше примере это неизвестные x ₁, x ₂, x ₃. Остальные неизвестные называются свободными. В рассмотренном выше примере это неизвестные x ₄, и x ₅. Свободным неизвестным можно придавать любые значения или выражать их через параметры, как это сделано в последнем примере.

Базисные неизвестные единственным образом выражаются через свободные неизвестные.

Если свободным неизвестным приданы конкретные числовые значения и через них выражены базисные неизвестные, то полученное решение называется частным решением.

Если свободные неизвестные выражены через параметры, то получается решение, которое называется общим решением.

Все бесконечное множество решений системы можно получить, придавая свободным неизвестным любые числовые значения и находя соответствующие значения базисных неизвестных.

Если всем свободным неизвестным приданы нулевые значения, то полученное решение называется базисным.

Одну и ту же систему иногда можно привести к разным наборам базисных неизвестных. Так, например, можно поменять местами 3-й и 4-й столбцы в матрице (6). Тогда базисными будут неизвестные x ₁, x ₂, x ₄, а свободными – x ₃ и x ₅. Если получены два различных набора базисных неизвестных при различных способах нахождения решения одной и той же системы, то эти наборы обязательно содержат одно и то же число неизвестных, называемое рангом системы.

Сформулируем теперь кратко суть метода Гаусса. Полагая, что в системе коэффициент a ₁₁ отличен от нуля (если это не так, то следует на первое место поставить уравнение с отличным от нуля коэффициентом при x ₁ и переобозначить коэффициенты), преобразуем систему следующим образом: первое уравнение оставляем без изменения, а из всех остальных уравнений исключаем неизвестную x ₁ с помощью эквивалентных преобразований описанным выше способом.

В полученной системе

,

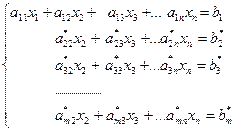считая, что 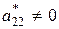(что всегда можно получить, переставив уравнения или слагаемые внутри уравнений и переобозначив коэффициенты системы), оставляем без изменений первые два уравнения системы, а из остальных уравнений, используя второе уравнения, с помощью элементарных преобразований исключаем неизвестную x ₂. Во вновь полученной системе

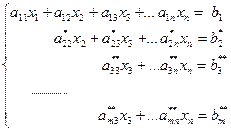
при условии 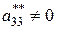оставляем без изменений первые три уравнения, а из всех остальных с помощью третьего уравнения элементарными преобразованиями исключаем неизвестную x ₃.

Этот процесс продолжается до тех пор, пока не реализуется один из трех возможных случаев:

1) если в результате приходим к системе, одно из уравнений которой имеет нулевые коэффициенты при всех неизвестных и отличный от нуля свободный член, то исходная система несовместна;

2) если в результате преобразований получаем систему с матрицей коэффициентов треугольного вида, то система совместна и является определенной;

3) если получается система с трапецеидальной матрицей коэффициентов (и при этом не выполняется условие пункта 1), то система совместна и неопределенна.

Дата добавления: 2014-12-24